CS 294-1
Mesh Generation and Geometry Processing in
Graphics, Engineering, and Modeling
Jonathan Shewchuk
![]()
Spring 2008
Mondays and Wednesday, 5:30-7:00 pm
320 Soda Hall

|
(Course icon, at left, is courtesy of
Nina Amenta.)
CS 294-1
Jonathan Shewchuk |
The only prerequisite is a thorough familiarity with fundamental data structures (CS 61B or the equivalent).
Topics include:
 Jules Bloomenthal,
An Implicit Surface Polygonizer,
Graphics Gems IV, Paul Heckbert (editor), pages 324-349,
Academic Press (Boston, Massachusetts), 1994.
PDF (634k).
To save paper, print only the first 8 pages.
The rest is code.
Jules Bloomenthal,
An Implicit Surface Polygonizer,
Graphics Gems IV, Paul Heckbert (editor), pages 324-349,
Academic Press (Boston, Massachusetts), 1994.
PDF (634k).
To save paper, print only the first 8 pages.
The rest is code.
 William E. Lorensen and Harvey E. Cline,
Marching Cubes:
A High Resolution 3D Surface Construction Algorithm,
Computer Graphics (SIGGRAPH ’87 Proceedings) (Anaheim, California),
pages 163-170, July 1987.
Read Section 4.
William E. Lorensen and Harvey E. Cline,
Marching Cubes:
A High Resolution 3D Surface Construction Algorithm,
Computer Graphics (SIGGRAPH ’87 Proceedings) (Anaheim, California),
pages 163-170, July 1987.
Read Section 4.
 Optional web page, good for the pictures.
James Sharman,
The Marching Cubes
Algorithm.
Optional web page, good for the pictures.
James Sharman,
The Marching Cubes
Algorithm.
 Optional. This paper solves the problem of holes
in the triangulated surfaces produced by the original marching cubes algorithm.
I discuss it briefly in class, but it's not required reading.
Gregory M. Nielson and Bernd Hamann,
The Asymptotic
Decider: Resolving the Ambiguity in Marching Cubes,
Proceedings of the 2nd Conference on Visualization ’91
(San Diego, California), pages 83-91, October 1991.
PDF (23,696k).
Optional. This paper solves the problem of holes
in the triangulated surfaces produced by the original marching cubes algorithm.
I discuss it briefly in class, but it's not required reading.
Gregory M. Nielson and Bernd Hamann,
The Asymptotic
Decider: Resolving the Ambiguity in Marching Cubes,
Proceedings of the 2nd Conference on Visualization ’91
(San Diego, California), pages 83-91, October 1991.
PDF (23,696k).
 Tao Ju, Frank Losasso, Scott Schaefer, and Joe Warren,
Dual
Contouring of Hermite Data,
Proceedings of SIGGRAPH 2002 (San Antonio, Texas), pages 339-346, July 2002.
Skip the discussions of QR decompositions
(and ask me if you want to know a better way to obtain numerical stability).
Section 4 is optional reading, but good reading.
Tao Ju, Frank Losasso, Scott Schaefer, and Joe Warren,
Dual
Contouring of Hermite Data,
Proceedings of SIGGRAPH 2002 (San Antonio, Texas), pages 339-346, July 2002.
Skip the discussions of QR decompositions
(and ask me if you want to know a better way to obtain numerical stability).
Section 4 is optional reading, but good reading.
 Optional. You might want this if you ever implement dual contouring.
Scott Schaefer and Joe Warren,
Dual Contouring: “The Secret Sauce,”
Technical Report TR02-408, Department of Computer Science, Rice University,
2002.
PDF (376k).
Optional. You might want this if you ever implement dual contouring.
Scott Schaefer and Joe Warren,
Dual Contouring: “The Secret Sauce,”
Technical Report TR02-408, Department of Computer Science, Rice University,
2002.
PDF (376k).
 Marshall Bern and David Eppstein,
Mesh Generation and Optimal Triangulation,
pages 23-90 of Computing in Euclidean Geometry,
Ding-Zhu Du and Frank Hwang (editors), World Scientific, Singapore, 1992.
PostScript (937k) or
PDF (1,120k).
Read pages 1-7.
Over the semester, we'll read most of this survey.
Marshall Bern and David Eppstein,
Mesh Generation and Optimal Triangulation,
pages 23-90 of Computing in Euclidean Geometry,
Ding-Zhu Du and Frank Hwang (editors), World Scientific, Singapore, 1992.
PostScript (937k) or
PDF (1,120k).
Read pages 1-7.
Over the semester, we'll read most of this survey.
 Herbert Edelsbrunner,
Geometry and Topology of Grid Generation,
lecture notes, Spring 1999.
Meeting 6: Simplicial Complexes
(PostScript, 137k or
PDF, 135k) and
Meeting 7: Spaces and Manifolds
(PostScript, 120k or
PDF, 115k).
Skip the “Nerves” section.
Don't worry if you don't understand the “Topological spaces”
section; replace that with the (more intuitive) metric spaces I teach in class.
Herbert Edelsbrunner,
Geometry and Topology of Grid Generation,
lecture notes, Spring 1999.
Meeting 6: Simplicial Complexes
(PostScript, 137k or
PDF, 135k) and
Meeting 7: Spaces and Manifolds
(PostScript, 120k or
PDF, 115k).
Skip the “Nerves” section.
Don't worry if you don't understand the “Topological spaces”
section; replace that with the (more intuitive) metric spaces I teach in class.
 Edge flip cookie courtesy of Bryan Klingner |
Lecture 5 (February 6): The incremental insertion algorithm for constructing a Delaunay triangulation. Point location methods: walking, conflict graphs, bucketing. Biased randomized insertion orders.
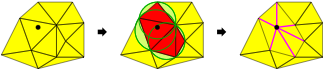 Lecture notes, pages to be written.
Lecture notes, pages to be written.
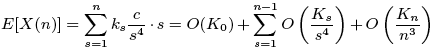 Optional.
Nina Amenta, Sunghee Choi, and Günter Rote.
Incremental Constructions con BRIO,
Proceedings of the Nineteenth Annual Symposium on Computational Geometry
(San Diego, California), pages 211-219, June 2003.
PDF (461k).
Everyone should know about the BRIO paper,
though I don't make it required reading for the class.
Even if you don't want to immerse yourself in the heartbreakingly elegant
analysis, Sections 1, 2, 7, 8, and 9 make good light reading.
Optional.
Nina Amenta, Sunghee Choi, and Günter Rote.
Incremental Constructions con BRIO,
Proceedings of the Nineteenth Annual Symposium on Computational Geometry
(San Diego, California), pages 211-219, June 2003.
PDF (461k).
Everyone should know about the BRIO paper,
though I don't make it required reading for the class.
Even if you don't want to immerse yourself in the heartbreakingly elegant
analysis, Sections 1, 2, 7, 8, and 9 make good light reading.
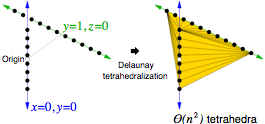 Lecture notes, pages to be written.
Lecture notes, pages to be written.
 Daniel K. Blandford, Guy E. Blelloch, David E. Cardoze, and Clemens Kadow,
Compact Representations of Simplicial Meshes in Two and
Three Dimensions,
International Journal of Computational Geometry and Applications
15(1):3-24, February 2005.
PDF (2,364k).
Daniel K. Blandford, Guy E. Blelloch, David E. Cardoze, and Clemens Kadow,
Compact Representations of Simplicial Meshes in Two and
Three Dimensions,
International Journal of Computational Geometry and Applications
15(1):3-24, February 2005.
PDF (2,364k).
 Optional.
Leonidas J. Guibas and Jorge Stolfi,
Primitives for the Manipulation of General Subdivisions and
the Computation of Voronoi Diagrams,
ACM Transactions on Graphics 4(2):74-123, April 1985.
This paper discusses an edge-based data structure called
the quad-edge, which simultaneously represents a planar subdivision
and its dual (e.g. a Delaunay triangulation and a Voronoi diagram).
It also gives pseudocode for the divide-and-conquer
and incremental insertion (with a not-so-good version of walking point
location) algorithms for constructing Delaunay triangulations.
Section 9 or 10 might help you with Project I (though I want
you to use the Blandford-Blelloch-Cardoze-Kadow data structure).
The rest of the paper is pretty interesting too, but you'll probably
want to skip Section 3.
Optional.
Leonidas J. Guibas and Jorge Stolfi,
Primitives for the Manipulation of General Subdivisions and
the Computation of Voronoi Diagrams,
ACM Transactions on Graphics 4(2):74-123, April 1985.
This paper discusses an edge-based data structure called
the quad-edge, which simultaneously represents a planar subdivision
and its dual (e.g. a Delaunay triangulation and a Voronoi diagram).
It also gives pseudocode for the divide-and-conquer
and incremental insertion (with a not-so-good version of walking point
location) algorithms for constructing Delaunay triangulations.
Section 9 or 10 might help you with Project I (though I want
you to use the Blandford-Blelloch-Cardoze-Kadow data structure).
The rest of the paper is pretty interesting too, but you'll probably
want to skip Section 3.
Lecture 8 (February 20): Constrained Delaunay triangulations. Comparison of Delaunay triangulation algorithms. Geometric predicates and geometric robustness.
 Lecture notes,
pages 10-16.
Lecture notes,
pages 10-16.
 My Lecture Notes on Geometric Robustness.
Gnuzipped PostScript (125k)
or
PDF (213k).
Read Sections 2-3.2.
Make sure you know what's in Section 3 in case you ever need it as a reference.
It might help you implement your projects.
Section 1 is entirely optional.
My Lecture Notes on Geometric Robustness.
Gnuzipped PostScript (125k)
or
PDF (213k).
Read Sections 2-3.2.
Make sure you know what's in Section 3 in case you ever need it as a reference.
It might help you implement your projects.
Section 1 is entirely optional.
 Jonathan Richard Shewchuk,
What Is a Good Linear Element?
Interpolation, Conditioning, and Quality Measures,
Eleventh International Meshing Roundtable (Ithaca, New York),
pages 115-126, Sandia National Laboratories, September 2002.
PostScript (1,083k) or
PDF (250k).
Jonathan Richard Shewchuk,
What Is a Good Linear Element?
Interpolation, Conditioning, and Quality Measures,
Eleventh International Meshing Roundtable (Ithaca, New York),
pages 115-126, Sandia National Laboratories, September 2002.
PostScript (1,083k) or
PDF (250k).
 Bern and Eppstein,
pages 38-45, 62-64.
Bern and Eppstein,
pages 38-45, 62-64.
 Lecture notes, pages to be written.
Lecture notes, pages to be written.
 Lecture notes, pages 41-59.
Lecture notes, pages 41-59.
 Optional.
Jim Ruppert, A Delaunay Refinement Algorithm for Quality 2-Dimensional
Mesh Generation, Journal of Algorithms 18(3):548-585, May 1995.
PostScript (192k) or
PDF (443k).
This material is mostly covered in
the lecture notes, but Ruppert's original paper is excellent.
Optional.
Jim Ruppert, A Delaunay Refinement Algorithm for Quality 2-Dimensional
Mesh Generation, Journal of Algorithms 18(3):548-585, May 1995.
PostScript (192k) or
PDF (443k).
This material is mostly covered in
the lecture notes, but Ruppert's original paper is excellent.
 David L. Marcum,
Unstructured Grid Generation Using Automatic Local Point Insertion
and Local Reconnection,
Chapter 18 of Handbook of Grid Generation
(Joe F. Thompson, Bharat K. Soni, and Nigel P. Weatherill, editors),
CRC Press, 1999.
Only Sections 18.1 and 18.2 are required reading,
but Section 18.6 is also recommended because it so concisely summarizes many of
the common concerns of engineering mesh generation papers.
Some translations:
Marcum's “local reconnection” is our bistellar flips.
Marcum's “direct subdivision” is our lazy vertex insertion.
David L. Marcum,
Unstructured Grid Generation Using Automatic Local Point Insertion
and Local Reconnection,
Chapter 18 of Handbook of Grid Generation
(Joe F. Thompson, Bharat K. Soni, and Nigel P. Weatherill, editors),
CRC Press, 1999.
Only Sections 18.1 and 18.2 are required reading,
but Section 18.6 is also recommended because it so concisely summarizes many of
the common concerns of engineering mesh generation papers.
Some translations:
Marcum's “local reconnection” is our bistellar flips.
Marcum's “direct subdivision” is our lazy vertex insertion.
 François Labelle and Jonathan Richard Shewchuk,
Isosurface Stuffing: Fast Tetrahedral Meshes with Good Dihedral Angles,
ACM Transactions on Graphics 26(3), August 2007.
Special issue on Proceedings of SIGGRAPH 2007.
PDF (3,530k).
François Labelle and Jonathan Richard Shewchuk,
Isosurface Stuffing: Fast Tetrahedral Meshes with Good Dihedral Angles,
ACM Transactions on Graphics 26(3), August 2007.
Special issue on Proceedings of SIGGRAPH 2007.
PDF (3,530k).
 Bern and Eppstein,
pages 14-18, 45-47.
There's a rather important typo in the middle of Page 18:
the sentence beginning,
“We compute these values in increasing order of i...”
should read “in decreasing order of i.”
Bern and Eppstein,
pages 14-18, 45-47.
There's a rather important typo in the middle of Page 18:
the sentence beginning,
“We compute these values in increasing order of i...”
should read “in decreasing order of i.”
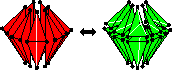 My unpublished tutorial,
Two Discrete Optimization Algorithms for the Topological Improvement
of Tetrahedral Meshes, 2002.
PostScript (295k) or
PDF (168k).
Section 2 discusses Klincsek's dynamic programming algorithm for
optimal triangulation of polygons in detail, and shows how to use it to perform
edge removal operations to improve tetrahedral meshes.
My unpublished tutorial,
Two Discrete Optimization Algorithms for the Topological Improvement
of Tetrahedral Meshes, 2002.
PostScript (295k) or
PDF (168k).
Section 2 discusses Klincsek's dynamic programming algorithm for
optimal triangulation of polygons in detail, and shows how to use it to perform
edge removal operations to improve tetrahedral meshes.
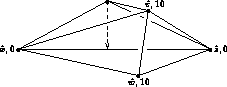 Marshall Bern, Herbert Edelsbrunner, David Eppstein, Scott Mitchell,
and Tiow Seng Tan,
Edge Insertion for Optimal Triangulations,
Discrete & Computational Geometry 10:47-65, 1993.
Gnuzipped PostScript (72k) or
PDF (245k).
Marshall Bern, Herbert Edelsbrunner, David Eppstein, Scott Mitchell,
and Tiow Seng Tan,
Edge Insertion for Optimal Triangulations,
Discrete & Computational Geometry 10:47-65, 1993.
Gnuzipped PostScript (72k) or
PDF (245k).
 Lori A. Freitag and Carl Ollivier-Gooch,
Tetrahedral Mesh Improvement Using Swapping and Smoothing,
International Journal for Numerical Methods in Engineering 40:3979-4002,
1997.
Gnuzipped PostScript (223k) or
PDF (359k).
Lori A. Freitag and Carl Ollivier-Gooch,
Tetrahedral Mesh Improvement Using Swapping and Smoothing,
International Journal for Numerical Methods in Engineering 40:3979-4002,
1997.
Gnuzipped PostScript (223k) or
PDF (359k).
 Bryan Matthew Klingner and Jonathan Richard Shewchuk,
Aggressive Tetrahedral Mesh Improvement,
Proceedings of the 16th International Meshing Roundtable (Seattle, Washington),
pages 3-23, October 2007.
PDF (26,567k).
Bryan's talk in PDF (36,723k).
Bryan Matthew Klingner and Jonathan Richard Shewchuk,
Aggressive Tetrahedral Mesh Improvement,
Proceedings of the 16th International Meshing Roundtable (Seattle, Washington),
pages 3-23, October 2007.
PDF (26,567k).
Bryan's talk in PDF (36,723k).
 Tamal K. Dey and Piyush Kumar,
A Simple Provable Algorithm for Curve Reconstruction,
Proceedings of the Tenth Annual Symposium on Discrete Algorithms
(Baltimore, Maryland), pages 893-894, January 1999.
Gnuzipped PostScript (88k) or
PDF (151k).
Tamal K. Dey and Piyush Kumar,
A Simple Provable Algorithm for Curve Reconstruction,
Proceedings of the Tenth Annual Symposium on Discrete Algorithms
(Baltimore, Maryland), pages 893-894, January 1999.
Gnuzipped PostScript (88k) or
PDF (151k).
 Optional.
My lecture includes Lemma 1 from this pioneering paper,
which Dey and Kumar use in their correctness proof.
Nina Amenta, Marshall Bern, and David Eppstein,
The Crust and the Beta-Skeleton: Combinatorial Curve Reconstruction,
Graphical Models and Image Processing 60/2(2):125-135, 1998.
Gnuzipped PostScript (134k) or
PDF (326k).
Optional.
My lecture includes Lemma 1 from this pioneering paper,
which Dey and Kumar use in their correctness proof.
Nina Amenta, Marshall Bern, and David Eppstein,
The Crust and the Beta-Skeleton: Combinatorial Curve Reconstruction,
Graphical Models and Image Processing 60/2(2):125-135, 1998.
Gnuzipped PostScript (134k) or
PDF (326k).
 Nina Amenta, Sunghee Choi, Tamal K. Dey, and N. Leekha,
A Simple Algorithm for Homeomorphic Surface Reconstruction,
International Journal of Computational Geometry and Applications
12(1-2):125-141, 2002.
PDF (2,151k).
Feel free to skip the proofs
(but read the theorems).
Nina Amenta, Sunghee Choi, Tamal K. Dey, and N. Leekha,
A Simple Algorithm for Homeomorphic Surface Reconstruction,
International Journal of Computational Geometry and Applications
12(1-2):125-141, 2002.
PDF (2,151k).
Feel free to skip the proofs
(but read the theorems).
 Optional.
Herbert Edelsbrunner,
Surface Reconstruction by Wrapping Finite Sets in Space,
pages 379-404 of
Discrete and Computational Geometry: The Goodman-Pollack Festschrift,
Boris Aronov (editor), Springer-Verlag, 2003.
PDF (400k).
Better known as the Wrap algorithm.
Be warned that some heavy translation is required to get from this paper
to how I describe it in lecture.
Optional.
Herbert Edelsbrunner,
Surface Reconstruction by Wrapping Finite Sets in Space,
pages 379-404 of
Discrete and Computational Geometry: The Goodman-Pollack Festschrift,
Boris Aronov (editor), Springer-Verlag, 2003.
PDF (400k).
Better known as the Wrap algorithm.
Be warned that some heavy translation is required to get from this paper
to how I describe it in lecture.
 Optional.
Tamal Krishna Dey,
Curve and Surface Reconstruction:
Algorithms with Mathematical Analysis,
Cambridge University Press, New York, 2007.
The
preface, contents, Chapters 3 and 4, and errata.
This book is your one-stop shop for everything in Lectures 15 and 16.
Restricted Delaunay triangulations on pages 21-23 and 50-57;
the NN-Crust algorithm in Section 2.3 (with proofs in Section 2.1);
the Cocone algorithm in Chapter 4 (with proofs in Chapter 3);
the Wrap algorithm in Chapter 10.
Optional.
Tamal Krishna Dey,
Curve and Surface Reconstruction:
Algorithms with Mathematical Analysis,
Cambridge University Press, New York, 2007.
The
preface, contents, Chapters 3 and 4, and errata.
This book is your one-stop shop for everything in Lectures 15 and 16.
Restricted Delaunay triangulations on pages 21-23 and 50-57;
the NN-Crust algorithm in Section 2.3 (with proofs in Section 2.1);
the Cocone algorithm in Chapter 4 (with proofs in Chapter 3);
the Wrap algorithm in Chapter 10.
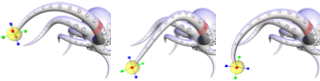
Lecture 17 (March 31): Surface mesh editing. Laplacian coordinates. Rotation-invariant mesh representation.
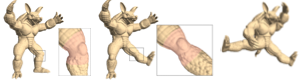 Yaron Lipman, Olga Sorkine, Daniel Cohen-Or and David Levin,
Linear Rotation-Invariant Coordinates for Meshes,
ACM Transactions on Graphics 24(3):479-487, July 2005.
PDF (8,080 k).
Special issue on Proceedings of SIGGRAPH 2005.
Read Sections 1 and 4.
If you make it to lecture, you can probably skip Sections 2 and 3:
in class, I will simplify the formulation and notation a lot,
and skip the discrete forms (but don't skip the discrete frames).
Discrete forms are useful if you want a compact encoding or
an understanding of the relationship to continuous differential geometry,
but they aren't necessary to do mesh editing.
If you don't catch my lecture, make sure you understand equations (2) and (5).
Yaron Lipman, Olga Sorkine, Daniel Cohen-Or and David Levin,
Linear Rotation-Invariant Coordinates for Meshes,
ACM Transactions on Graphics 24(3):479-487, July 2005.
PDF (8,080 k).
Special issue on Proceedings of SIGGRAPH 2005.
Read Sections 1 and 4.
If you make it to lecture, you can probably skip Sections 2 and 3:
in class, I will simplify the formulation and notation a lot,
and skip the discrete forms (but don't skip the discrete frames).
Discrete forms are useful if you want a compact encoding or
an understanding of the relationship to continuous differential geometry,
but they aren't necessary to do mesh editing.
If you don't catch my lecture, make sure you understand equations (2) and (5).
 Optional.
Olga Sorkine, Daniel Cohen-Or, Yaron Lipman, Marc Alexa,
Christian Rössl, and Hans-Peter Seidel,
Laplacian Surface Editing,
Symposium on Geometry Processing 2004 (Nice, France),
Eurographics Association, pages 179-188, July 2004.
PDF (9,601 k).
If you read this, skip everything
involving the transformation Ti—i.e.
from the paragraph following equation (4) to the end of Section 3.1.
The problem that Ti is meant to solve is
better handled by the paper above.
Optional.
Olga Sorkine, Daniel Cohen-Or, Yaron Lipman, Marc Alexa,
Christian Rössl, and Hans-Peter Seidel,
Laplacian Surface Editing,
Symposium on Geometry Processing 2004 (Nice, France),
Eurographics Association, pages 179-188, July 2004.
PDF (9,601 k).
If you read this, skip everything
involving the transformation Ti—i.e.
from the paragraph following equation (4) to the end of Section 3.1.
The problem that Ti is meant to solve is
better handled by the paper above.
 Ted D. Blacker and Michael B. Stephenson,
Paving:
A New Approach to Automated Quadrilateral Mesh Generation,
International Journal for Numerical Methods in Engineering
32(4):811-847, September 1991.
Erratum:
Equation (20) should end with
“ε1 > ε2”.
Ted D. Blacker and Michael B. Stephenson,
Paving:
A New Approach to Automated Quadrilateral Mesh Generation,
International Journal for Numerical Methods in Engineering
32(4):811-847, September 1991.
Erratum:
Equation (20) should end with
“ε1 > ε2”.
Lecture 19 (April 7): Student presentations: Jessica Schoen on provably good anisotropic Voronoi diagrams. Nuttapong Chentanez on variational tetrahedral meshing. Mini-lecture on polygon triangulation by finding diagonals.
 François Labelle and Jonathan Richard Shewchuk,
Anisotropic Voronoi Diagrams and
Guaranteed-Quality Anisotropic Mesh Generation,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 191-200,
Association for Computing Machinery, June 2003.
PostScript (910k) or
PDF (284k).
Jessica's talk in PowerPoint (5,278k).
Slides from a related
talk (PDF, 1,301k) are also available.
François Labelle and Jonathan Richard Shewchuk,
Anisotropic Voronoi Diagrams and
Guaranteed-Quality Anisotropic Mesh Generation,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 191-200,
Association for Computing Machinery, June 2003.
PostScript (910k) or
PDF (284k).
Jessica's talk in PowerPoint (5,278k).
Slides from a related
talk (PDF, 1,301k) are also available.
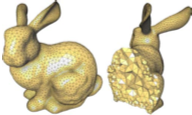 Pierre Alliez, David Cohen-Steiner, Mariette Yvinec, and Mathieu Desbrun,
Variational Tetrahedral Meshing,
ACM Transactions on Graphics 24(3):617-625, 2005.
Special issue on Proceedings of SIGGRAPH 2005.
PDF (778k).
Nuttapong's talk in PDF (22,064k).
Pierre Alliez, David Cohen-Steiner, Mariette Yvinec, and Mathieu Desbrun,
Variational Tetrahedral Meshing,
ACM Transactions on Graphics 24(3):617-625, 2005.
Special issue on Proceedings of SIGGRAPH 2005.
PDF (778k).
Nuttapong's talk in PDF (22,064k).
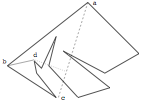 Bern and Eppstein,
pages 6-7.
Bern and Eppstein,
pages 6-7.
 Christian Früh, Siddharth Jain, and Avideh Zakhor,
Data Processing Algorithms for Generating Textured 3D Building Facade
Meshes from Laser Scans and Camera Images,
International Journal of Computer Vision 61(2):159-184,
February 2005.
PDF (5,778k).
Ilya's talk in PDF (2,383k).
Christian Früh, Siddharth Jain, and Avideh Zakhor,
Data Processing Algorithms for Generating Textured 3D Building Facade
Meshes from Laser Scans and Camera Images,
International Journal of Computer Vision 61(2):159-184,
February 2005.
PDF (5,778k).
Ilya's talk in PDF (2,383k).
 Michael Garland and Paul Heckbert,
Surface Simplification Using Quadric Error Metrics,
Computer Graphics (SIGGRAPH '97 Proceedings), August 1997.
PostScript (2,328k) or
PDF (390k).
Slides from their
talk (PDF, 601k) are also available.
Michael Garland and Paul Heckbert,
Surface Simplification Using Quadric Error Metrics,
Computer Graphics (SIGGRAPH '97 Proceedings), August 1997.
PostScript (2,328k) or
PDF (390k).
Slides from their
talk (PDF, 601k) are also available.
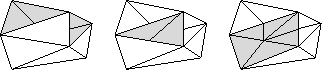 Marshall Bern and Paul Plassmann, Mesh Generation,
Chapter 6 of Handbook of Computational Geometry,
Jörg-Rüdiger Sack and Jorge Urrutia (editors), Elsevier Science,
1999.
Gnuzipped PostScript (961k) or
PDF (1,231k).
Read pages 16-18, 30-31 (on mesh refinement).
Marshall Bern and Paul Plassmann, Mesh Generation,
Chapter 6 of Handbook of Computational Geometry,
Jörg-Rüdiger Sack and Jorge Urrutia (editors), Elsevier Science,
1999.
Gnuzipped PostScript (961k) or
PDF (1,231k).
Read pages 16-18, 30-31 (on mesh refinement).
 Optional. Sections 1, 2, 3, and 6 are recommended reading.
(The proofs, in Sections 4 and 5, are more difficult.)
Gary L. Miller, Dafna Talmor, and Shang-Hua Teng,
Optimal Good-Aspect-Ratio Coarsening for Unstructured Meshes,
Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms
(New Orleans, Louisiana), January 1997.
Gnuzipped PostScript (263k) or
PDF (421k).
Optional. Sections 1, 2, 3, and 6 are recommended reading.
(The proofs, in Sections 4 and 5, are more difficult.)
Gary L. Miller, Dafna Talmor, and Shang-Hua Teng,
Optimal Good-Aspect-Ratio Coarsening for Unstructured Meshes,
Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms
(New Orleans, Louisiana), January 1997.
Gnuzipped PostScript (263k) or
PDF (421k).
 Scott Schaefer and Joe Warren,
Dual Marching Cubes: Primal Contouring of Dual Grids,
Computer Graphics Forum 24(2):195-201, 2005.
PDF (1,037k).
Jimmy's talk in PDF (1,849k).
Scott Schaefer and Joe Warren,
Dual Marching Cubes: Primal Contouring of Dual Grids,
Computer Graphics Forum 24(2):195-201, 2005.
PDF (1,037k).
Jimmy's talk in PDF (1,849k).
 Mathieu Desbrun, Mark Meyer, Peter Schröder, and Alan H. Barr,
Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow,
Computer Graphics (SIGGRAPH ’99 Proceedings) (Los Angeles, California),
pages 317-324, August 1999.
PDF (1,735k).
Darsh's talk in PDF (794k).
Mathieu Desbrun, Mark Meyer, Peter Schröder, and Alan H. Barr,
Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow,
Computer Graphics (SIGGRAPH ’99 Proceedings) (Los Angeles, California),
pages 317-324, August 1999.
PDF (1,735k).
Darsh's talk in PDF (794k).
 Paul Kinney,
CleanUp: Improving Quadrilateral Finite Element Meshes,
Sixth International Meshing Roundtable (Park City, Utah),
pages 449-461, October 1997.
Gnuzipped PostScript (40k) or
PDF (36k).
James' talk in PDF (910k).
Paul Kinney,
CleanUp: Improving Quadrilateral Finite Element Meshes,
Sixth International Meshing Roundtable (Park City, Utah),
pages 449-461, October 1997.
Gnuzipped PostScript (40k) or
PDF (36k).
James' talk in PDF (910k).
 Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes, Computer Graphics
(SIGGRAPH ’97 Proceedings), pages 189-198, August 1997.
Gnuzipped PostScript (3,891k) or
PDF (601k).
Peter's talk in PDF (11,169k).
Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes, Computer Graphics
(SIGGRAPH ’97 Proceedings), pages 189-198, August 1997.
Gnuzipped PostScript (3,891k) or
PDF (601k).
Peter's talk in PDF (11,169k).
 Lecture Notes on Delaunay Mesh Generation, Chapter 4.
Lecture Notes on Delaunay Mesh Generation, Chapter 4.
 Fakir S. Nooruddin and Greg Turk,
Simplification and Repair of Polygonal Meshes Using Volumetric
Techniques,
IEEE Transactions on Visualization and Computer Graphics 9(2):191-205,
April-June 2003.
PDF (14,745k).
Siyu's talk in
Google
Docs or PDF (2,055k).
Fakir S. Nooruddin and Greg Turk,
Simplification and Repair of Polygonal Meshes Using Volumetric
Techniques,
IEEE Transactions on Visualization and Computer Graphics 9(2):191-205,
April-June 2003.
PDF (14,745k).
Siyu's talk in
Google
Docs or PDF (2,055k).
 Optional.
L. Paul Chew,
Guaranteed-Quality Mesh Generation for Curved Surfaces,
Proceedings of the Ninth Annual Symposium on Computational Geometry
(San Diego, California), pages 274-280, May 1993.
Although he didn't know it at the time,
Chew's definition of Delaunay edge flips on curved surfaces is consistent with
the restricted Delaunay triangulation.
Optional.
L. Paul Chew,
Guaranteed-Quality Mesh Generation for Curved Surfaces,
Proceedings of the Ninth Annual Symposium on Computational Geometry
(San Diego, California), pages 274-280, May 1993.
Although he didn't know it at the time,
Chew's definition of Delaunay edge flips on curved surfaces is consistent with
the restricted Delaunay triangulation.
 Tao Ju, Scott Schaefer, and Joe Warren,
Mean Value Coordinates for Closed Triangular Meshes,
ACM Transactions on Graphics 24(3):561-566, July 2005.
Special issue on Proceedings of SIGGRAPH 2005.
PDF (1,743k).
Tao Ju, Scott Schaefer, and Joe Warren,
Mean Value Coordinates for Closed Triangular Meshes,
ACM Transactions on Graphics 24(3):561-566, July 2005.
Special issue on Proceedings of SIGGRAPH 2005.
PDF (1,743k).
 David Cardoze, Alexandre Cunha, Gary L. Miller, Todd Phillips, and
Noel Walkington,
A Bézier-Based Approach to Unstructured Moving Meshes,
Twentieth Annual Symposium on Computational Geometry (Brooklyn, New York),
pages 310-319, June 2004.
PDF (691k).
Hagen's talk in PDF (694k).
David Cardoze, Alexandre Cunha, Gary L. Miller, Todd Phillips, and
Noel Walkington,
A Bézier-Based Approach to Unstructured Moving Meshes,
Twentieth Annual Symposium on Computational Geometry (Brooklyn, New York),
pages 310-319, June 2004.
PDF (691k).
Hagen's talk in PDF (694k).
 Pierre Alliez, David Cohen-Steiner, Olivier Devillers, Bruno Lévy,
and Mathieu Desbrun,
Anisotropic Polygonal Remeshing,
ACM Transactions on Graphics 22(3):485-493,
July 2003.
Special issue on Proceedings of SIGGRAPH 2003.
PDF (19,950k).
Dino's talk in PowerPoint (45,075k).
Pierre Alliez, David Cohen-Steiner, Olivier Devillers, Bruno Lévy,
and Mathieu Desbrun,
Anisotropic Polygonal Remeshing,
ACM Transactions on Graphics 22(3):485-493,
July 2003.
Special issue on Proceedings of SIGGRAPH 2003.
PDF (19,950k).
Dino's talk in PowerPoint (45,075k).
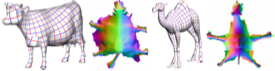 Alla Sheffer, Emil Praun, and Kenneth Rose,
Mesh Parameterization Methods and Their Applications,
Foundations and Trends in Computer Graphics and Vision 2(2):105-171,
2006.
PDF (15,635k).
Read Sections 1-3.
The rest is good too, but optional.
Alla Sheffer, Emil Praun, and Kenneth Rose,
Mesh Parameterization Methods and Their Applications,
Foundations and Trends in Computer Graphics and Vision 2(2):105-171,
2006.
PDF (15,635k).
Read Sections 1-3.
The rest is good too, but optional.
 Bern and Eppstein, pages 22-25, 40-41, 63.
Bern and Eppstein, pages 22-25, 40-41, 63.
 Mark S. Shephard, Hugues L. de Cougny, Robert M. O'Bara, and Mark W. Beall,
Automatic Grid Generation Using Spatially Based Trees,
Chapter 15 of Handbook of Grid Generation
(Joe F. Thompson, Bharat K. Soni, and Nigel P. Weatherill, editors),
CRC Press, 1999.
PDF (3,342k).
Mark S. Shephard, Hugues L. de Cougny, Robert M. O'Bara, and Mark W. Beall,
Automatic Grid Generation Using Spatially Based Trees,
Chapter 15 of Handbook of Grid Generation
(Joe F. Thompson, Bharat K. Soni, and Nigel P. Weatherill, editors),
CRC Press, 1999.
PDF (3,342k).
 Mark S. Shephard and Marcel K. Georges,
Automatic
Three-Dimensional Mesh Generation by the Finite Octree Technique,
International Journal for Numerical Methods in Engineering 32:709-749,
1991.
A strength of this paper is that the mesh generator is designed to work well
with CAD geometry representations (where the mesher must query a CAD program),
with all their numerical and topological flaws.
Mark S. Shephard and Marcel K. Georges,
Automatic
Three-Dimensional Mesh Generation by the Finite Octree Technique,
International Journal for Numerical Methods in Engineering 32:709-749,
1991.
A strength of this paper is that the mesh generator is designed to work well
with CAD geometry representations (where the mesher must query a CAD program),
with all their numerical and topological flaws.
 Marshall Bern, David Eppstein, and John R. Gilbert,
Provably Good Mesh Generation,
Journal of Computer and System Sciences 48(3):384-409, June 1994.
Gnuzipped PostScript (151k) or
PDF (341k).
This classic paper gives the first size-optimal guaranteed-quality
meshing algorithm (from before Ruppert invented his algorithm).
Marshall Bern, David Eppstein, and John R. Gilbert,
Provably Good Mesh Generation,
Journal of Computer and System Sciences 48(3):384-409, June 1994.
Gnuzipped PostScript (151k) or
PDF (341k).
This classic paper gives the first size-optimal guaranteed-quality
meshing algorithm (from before Ruppert invented his algorithm).
 (Man and Woman.
Fernand
Léger, 1881-1955.)
(Man and Woman.
Fernand
Léger, 1881-1955.)