
CS 294-5
Meshing and Triangulation in
Graphics, Engineering, and Modeling
Jonathan Shewchuk
Autumn 1999
Tuesdays and Thursdays, 2:00-3:30pm
606 Soda Hall

|
(Course icon, at left, is courtesy of
Nina Amenta.)
CS 294-5
Jonathan Shewchuk |
Student presentation requirement: Every student (including auditors) is asked to present a paper from this list of notable meshing publications. Please choose a presentation date by September 28. Please choose a paper at least a week before your presentation date.
The best related sites:
 Marshall Bern and David Eppstein,
Mesh Generation and Optimal Triangulation,
pp. 23-90 of Computing in Euclidean Geometry,
Ding-Zhu Du and Frank Hwang (editors), World Scientific, Singapore, 1992.
PostScript is available here.
Read pages 1-7.
Marshall Bern and David Eppstein,
Mesh Generation and Optimal Triangulation,
pp. 23-90 of Computing in Euclidean Geometry,
Ding-Zhu Du and Frank Hwang (editors), World Scientific, Singapore, 1992.
PostScript is available here.
Read pages 1-7.
 Lecture Notes on Delaunay Mesh Generation, pages 1-14.
PostScript is available here.
Lecture Notes on Delaunay Mesh Generation, pages 1-14.
PostScript is available here.
 (Optional. This material is mostly covered in the lecture notes,
but I include Ruppert's paper here for those who would like to see
the original source.)
Jim Ruppert, A Delaunay Refinement Algorithm for Quality 2-Dimensional
Mesh Generation, Journal of Algorithms 18(3):548-585, May 1995.
PostScript is available here.
(Optional. This material is mostly covered in the lecture notes,
but I include Ruppert's paper here for those who would like to see
the original source.)
Jim Ruppert, A Delaunay Refinement Algorithm for Quality 2-Dimensional
Mesh Generation, Journal of Algorithms 18(3):548-585, May 1995.
PostScript is available here.
 Mark S. Shephard, Hugues L. de Cougny, Robert M. O'Bara, and Mark W. Beall,
Automatic Grid Generation Using Spatially Based Trees,
Chapter 15 of Handbook of Grid Generation
(Joe F. Thompson, Bharat K. Soni, and Nigel P. Weatherill, editors),
CRC Press, 1999.
PDF (3,342k).
Mark S. Shephard, Hugues L. de Cougny, Robert M. O'Bara, and Mark W. Beall,
Automatic Grid Generation Using Spatially Based Trees,
Chapter 15 of Handbook of Grid Generation
(Joe F. Thompson, Bharat K. Soni, and Nigel P. Weatherill, editors),
CRC Press, 1999.
PDF (3,342k).
 Lecture Notes on Geometric Robustness.
PostScript is available here.
Sections 2 and 3 may help you implement your projects.
Lecture Notes on Geometric Robustness.
PostScript is available here.
Sections 2 and 3 may help you implement your projects.
 Lori A. Freitag and Carl Ollivier-Gooch,
Tetrahedral Mesh Improvement Using Swapping and Smoothing,
International Journal for Numerical Methods in Engineering 40:3979-4002,
1997.
PostScript is available here.
Lori A. Freitag and Carl Ollivier-Gooch,
Tetrahedral Mesh Improvement Using Swapping and Smoothing,
International Journal for Numerical Methods in Engineering 40:3979-4002,
1997.
PostScript is available here.
 Michael Garland and Paul Heckbert,
Surface Simplification Using Quadric Error Metrics,
Computer Graphics (SIGGRAPH '97 Proceedings), August 1997.
Michael Garland and Paul Heckbert,
Surface Simplification Using Quadric Error Metrics,
Computer Graphics (SIGGRAPH '97 Proceedings), August 1997.
 Timothy J. Tautges, Ted Blacker, and Scott Mitchell,
The Whisker Weaving Algorithm: A Connectivity-Based Method for Constructing
All-Hexahedral Finite Element Meshes.
Timothy J. Tautges, Ted Blacker, and Scott Mitchell,
The Whisker Weaving Algorithm: A Connectivity-Based Method for Constructing
All-Hexahedral Finite Element Meshes.
Lecture 15 (October 14): Surface mesh simplification. Topology-preserving edge contraction.
 Herbert Edelsbrunner,
Geometry and Topology of Grid Generation,
lecture notes, Spring 1999.
Meeting 9: Edge Contraction Algorithm
(PostScript),
Meeting 10: Preserving Topology
(PostScript), and
Meeting 12: Error Measure
(PostScript).
Herbert Edelsbrunner,
Geometry and Topology of Grid Generation,
lecture notes, Spring 1999.
Meeting 9: Edge Contraction Algorithm
(PostScript),
Meeting 10: Preserving Topology
(PostScript), and
Meeting 12: Error Measure
(PostScript).
 Nina Amenta, Marshall Bern, and David Eppstein,
The Crust and the Beta-Skeleton: Combinatorial Curve Reconstruction,
Graphical Models and Image Processing 60/2(2):125-135, 1998.
PostScript is available here. Skip Section 9.
Nina Amenta, Marshall Bern, and David Eppstein,
The Crust and the Beta-Skeleton: Combinatorial Curve Reconstruction,
Graphical Models and Image Processing 60/2(2):125-135, 1998.
PostScript is available here. Skip Section 9.
 Nina Amenta, Marshall Bern, and Manolis Kamvysselis,
A New Voronoi-Based Surface Reconstruction Algorithm,
Computer Graphics (SIGGRAPH '98 Proceedings), pages 415-421, July 1998.
PostScript is available here.
Nina Amenta, Marshall Bern, and Manolis Kamvysselis,
A New Voronoi-Based Surface Reconstruction Algorithm,
Computer Graphics (SIGGRAPH '98 Proceedings), pages 415-421, July 1998.
PostScript is available here.
 Robert W. Leland, Darryl J. Melander, Ray W. Meyers, Scott A. Mitchell,
and Timothy J. Tautges,
The Geode Algorithm: Combining Hex/Tet Plastering,
Dicing and Transition Elements
for Automatic, All-Hex Mesh Generation,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 515-521, October 1998.
Robert W. Leland, Darryl J. Melander, Ray W. Meyers, Scott A. Mitchell,
and Timothy J. Tautges,
The Geode Algorithm: Combining Hex/Tet Plastering,
Dicing and Transition Elements
for Automatic, All-Hex Mesh Generation,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 515-521, October 1998.
 Olivier Devillers,
Improved Incremental Randomized Delaunay Triangulation,
Proceedings of the Fourteenth Annual Symposium on Computation Geometry
(Minneapolis, Minnesota), pages 106-115, ACM, June 1998.
Olivier Devillers,
Improved Incremental Randomized Delaunay Triangulation,
Proceedings of the Fourteenth Annual Symposium on Computation Geometry
(Minneapolis, Minnesota), pages 106-115, ACM, June 1998.
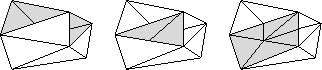 Marshall Bern and Paul Plassmann,
Mesh Generation, manuscript, 1997.
PostScript is available here.
Read pages 16-18, 30-31 (on mesh refinement).
Marshall Bern and Paul Plassmann,
Mesh Generation, manuscript, 1997.
PostScript is available here.
Read pages 16-18, 30-31 (on mesh refinement).
 Gary L. Miller, Dafna Talmor, and Shang-Hua Teng,
Optimal Good-Aspect-Ratio Coarsening for Unstructured Meshes,
Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms
(New Orleans, Louisiana), January 1997.
PostScript is available here.
Read Sections 1, 2, 3, and 6.
Gary L. Miller, Dafna Talmor, and Shang-Hua Teng,
Optimal Good-Aspect-Ratio Coarsening for Unstructured Meshes,
Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms
(New Orleans, Louisiana), January 1997.
PostScript is available here.
Read Sections 1, 2, 3, and 6.
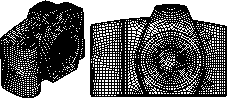 Steven J. Owen, Matthew L. Staten, Scott A. Canann, and Sunil Saigal,
Advancing Front Quadrilateral Meshing Using Triangle
Transformations,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 409-428, October 1998.
Steven J. Owen, Matthew L. Staten, Scott A. Canann, and Sunil Saigal,
Advancing Front Quadrilateral Meshing Using Triangle
Transformations,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 409-428, October 1998.
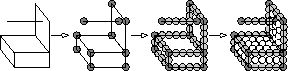 Kenji Shimada,
Anisotropic Triangular Meshing of Parametric Surfaces via
Close Packing of Ellipsoidal Bubbles,
Sixth International Meshing Roundtable (Park City, Utah),
pages 375-390, October 1997.
Kenji Shimada,
Anisotropic Triangular Meshing of Parametric Surfaces via
Close Packing of Ellipsoidal Bubbles,
Sixth International Meshing Roundtable (Park City, Utah),
pages 375-390, October 1997.
 Jovan Popovic and Hugues Hoppe,
Progressive Simplicial Complexes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 217-224, August 1997.
Jovan Popovic and Hugues Hoppe,
Progressive Simplicial Complexes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 217-224, August 1997.
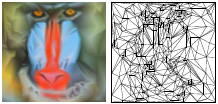 Michael Garland and Paul Heckbert,
Fast Triangular Approximation of Terrains and Height Fields,
manuscript, May 1997.
Michael Garland and Paul Heckbert,
Fast Triangular Approximation of Terrains and Height Fields,
manuscript, May 1997.
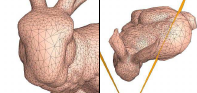 Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 189-198, August 1997.
Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes,
Computer Graphics (SIGGRAPH '97 Proceedings), pages 189-198, August 1997.
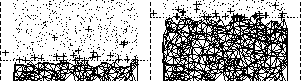 Peter Su and Robert L. Scot Drysdale,
A Comparison of Sequential Delaunay Triangulation Algorithms,
Proceedings of the Eleventh Annual Symposium on Computational Geometry
(Vancouver, British Columbia, Canada), pages 61-70, ACM, June 1995.
Peter Su and Robert L. Scot Drysdale,
A Comparison of Sequential Delaunay Triangulation Algorithms,
Proceedings of the Eleventh Annual Symposium on Computational Geometry
(Vancouver, British Columbia, Canada), pages 61-70, ACM, June 1995.
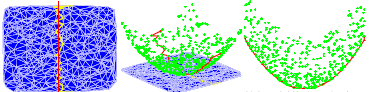 Guy E. Blelloch, Gary L. Miller, and Dafna Talmor,
Developing a Practical Projection-Based Parallel Delaunay Algorithm,
Proceedings of the Twelfth Annual Symposium on Computation Geometry
(Philadelphia, Pennsylvania), pages 186-195, ACM, May 1996.
Guy E. Blelloch, Gary L. Miller, and Dafna Talmor,
Developing a Practical Projection-Based Parallel Delaunay Algorithm,
Proceedings of the Twelfth Annual Symposium on Computation Geometry
(Philadelphia, Pennsylvania), pages 186-195, ACM, May 1996.
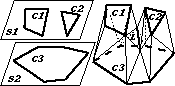 Chandrajit L. Bajaj, Edward J. Coyle, and Kwun-Nan Lin,
Surface and 3D Triangular Meshes from Planar Cross Sections,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 169-178, October 1996.
Chandrajit L. Bajaj, Edward J. Coyle, and Kwun-Nan Lin,
Surface and 3D Triangular Meshes from Planar Cross Sections,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 169-178, October 1996.
 Ted Blacker,
The Cooper Tool,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 13-29, October 1996.
Ted Blacker,
The Cooper Tool,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 13-29, October 1996.
 Brian Curless and Marc Levoy,
A Volumetric Method for Building Complex Models from Range Images,
Computer Graphics (SIGGRAPH '96 Proceedings), pages 303-312, 1996.
Brian Curless and Marc Levoy,
A Volumetric Method for Building Complex Models from Range Images,
Computer Graphics (SIGGRAPH '96 Proceedings), pages 303-312, 1996.
 Jarek Rossignac,
Edgebreaker: Connectivity Compression for Triangle Meshes,
Technical Report GIT-GVU-98-35, GVU Center, Georgia Institute of Technology,
October 1998.
Jarek Rossignac,
Edgebreaker: Connectivity Compression for Triangle Meshes,
Technical Report GIT-GVU-98-35, GVU Center, Georgia Institute of Technology,
October 1998.
Lecture 27 (December 2): Three-dimensional Delaunay refinement.
Topics include:
 (Man and Woman.
Fernand
Léger, 1881-1955.)
(Man and Woman.
Fernand
Léger, 1881-1955.)