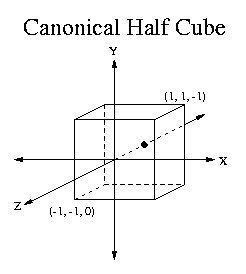
|
University of California, Berkeley EECS Dept, CS Division |
||
| Jordan Smith |
SLIDE: Scene Language for Interactive Dynamic Environments |
Prof. Carlo H. Séquin |
| Home | Goals | Publications | People | Gallery | Assignments | Distributions |
In this assignment, you are building slideortho3d, a 3D SLIDE viewer which handles parallel projections and flat shading of convex polygons. You will need to implement the following:
New options appear in bold.
You must implement 3D version of the matrix transformations. The supported transformations are 3D translations, 3D scaling, 3D rotations, and the special LookAt transformation. The LookAt transformation is convenient for placing cameras in your scene. The LookAt transformation is really a rigid body transformation which is the combination of a 3D rotation around an arbitrary axis and a translation. In the LookAt, you are given an eye point, a target position which you are looking at, and an up direction.
For more details read the 3D Transformation Notes. And see the notes about using Rodrigues' Formula for computing rotation matricies.
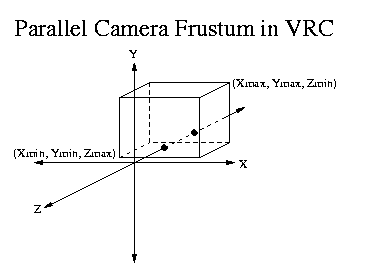
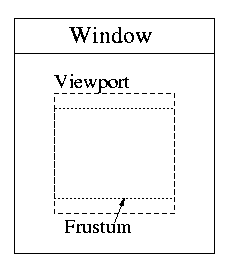
The camera object must create a projection matrix which maps points in View Reference Coordinates (VRC) to the Canonical Clipping Volume space. Then you will use the viewport mapping transform from the last assignment to map the clipped geometry to the viewport window. This is very similar to the viewport mapping process from the last assignment.
The volume defined by the camera frustum ([Xmin, Xmax], [Ymin, Ymax], [Zmin, Zmax]) is mapped to become the Canonical Half Cube ([-1, 1], [-1, 1], [-1, 0]) in Projection space. This is the VRC->PROJ transformation. Then the 2D viewport mapping is applied to the Half Cube preserving the Z values. This is the PROJ->VP transformation. The actual projection happens when the Z value is now dropped completing the parallel projection. The 2D vertices now define 2D polygons which can be rendered by OpenGL.
The following figures show the coordinate systems involved in the projection transformation and viewport mapping.
 |
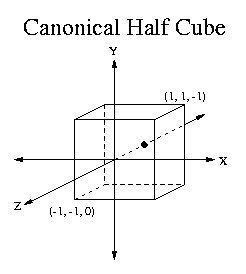 |
 |
| VRC | Canonical Half Cube | Viewport |
For more information on how to calculate the Gproj<-vrc read parallel projection section of the Camera Projection Notes.
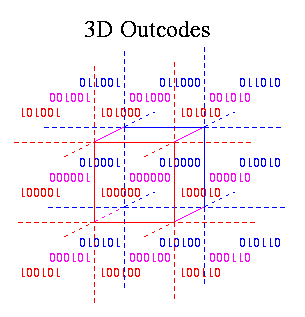
Extend your bounding box culling routines to work in 3D. You can easily extend the outcode idea to 3D where the outcodes become (forward, back, up, down, right, left). The diagram uses color to distinguish depth in the forward/back dimension Z.
Back face culling is when you do not render a polygon because its normal is pointing away from the viewer's eye point. A naive way of preforming this check would be to construct a vector from the eye point to a point on the face and compute the dot product of this line of sight vector and the normal vector. If this scalar is positive then the face is pointing away and consequently can be culled. A more sophisticated way of making this check is to transform the face's normal into the projection space, where the line of sight vector is always the negative Z-axis. Then the check for back face culling is just to see if the Z component of the transformed normal is negative.
Back face culling should never be preformed on objects which have
the SLF_HOLLOW solid flag, and it should not be preformed
if it is disabled in the rendering options.
For more details read the Back Face Culling Notes.
Extend your polygon clipping routines to work in 3D. In principle, it is the same algorithm just run over 6 half spaces with the addition of the near and far clipping planes instead of the 4 half spaces from 2D.
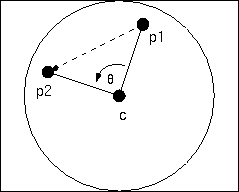
Each screen pixel over the crystal ball corresponds to a
point on the surface of the ball. Take the two vectors
from the center of the ball to the two picked surface points
v1 and
v2.
The axis should be orthogonal to those two vectors (cross
product) and the
angle of rotation should be the angle between them.
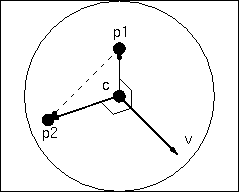
Any mouse motion outside the crystal ball should
result in pure z-rotation.
Don't worry about this unless you have everything else working!
In the great circle rotation interface, there is a dead
zone for radial mouse motion outside the crystal ball.
You can create some behavior by mapping those points
outside the ball to the back of the ball.
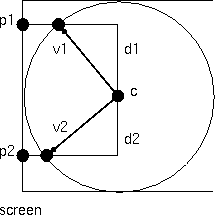
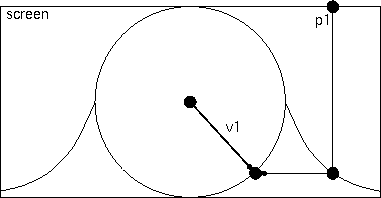
One way to do this is pictured on the right.
Suppose the crystal ball has a center at
(0,0,0) and a radius of 1.
Then any pixel that falls at a distance of
d > 1 from the center of the
screen misses the sphere.
That point should get mapped to
z = 1/d - 1,
then when you scale the x and y coordinates so that
(x,y,z) is a unit vector, you have the
point at the head of v1 on the back of the sphere.
Make a 3D dynamic scene ortho3d.slf which shows off your 3D rendering system.
Don't be timid with your transformations!
Make big moves in your scene, so that lot's of stuff get's clipped.
Your objects do not have to move in a physically realistic sense!
Follow the listed instructions for as5.
The SLIDE Implementation Specification gives information about the C++ class structure which implements the SLIDE viewer. It also gives an outline of the operation of the viewer.
This page was originally built by Jordan Smith.
Last modified: Thursday, 07-Oct-2004 11:10:25 PDT