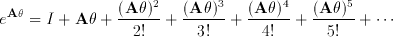
Suppose we are rotating a point, p, in space by an angle, b, (later also called theta) about an axis through the origin represented by the unit vector, a.
First, we create the matrix A which is the linear transformation that computes the cross product of the vector a with any other vector, v.
| a x v = |
| = |
|
| = Av, with A = |
|
Now, the rotation matrix can be written in terms of A as
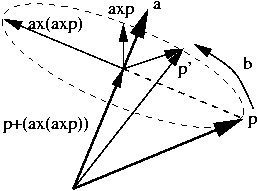
Suppose we are rotating a point, p, in space by an angle,
b, about an axis through the origin, represented by the unit
vector, a. The component of p parallel to a,
ppar a, will not change during the transformation.
The component of p perpendicular to a, pper a
will rotate about the axis in the plane perpendicular to the axis the same as in 2D
The vectors pper a and pbiper ar
of the correct length and orientation to act as the x and y vectors in this 2D rotation.
p' = ppar a + cos(b) pper a + sin(b) pbiper
p' = (p + (a x (a x p))) + cos(b) (-(a x (a x p))) + sin(b) (a x p)
p' = p + sin(b) (a x p) + [1 - cos(b)] (a x (a x p))
p' = (I + sin(b) A + [1 - cos(b)] A2) p
Suppose we are rotating a point, p, in space by an angle, b (called theta in the formatted equations), about an axis through the origin, represented by the unit vector, a. We will form a differential equation describing the motion of the point from time t=0 to time t=b. Let p(t} be the position of the point at time t. The velocity of the point at any time is
Now, if we use the matrix formula for cross products in our differential equation, we have a first order, linear system of differential equations, p'(t) = A p(t). The solution to that system is known to be p(t) = eAtp(0) so the location of the rotated point will be p(b) = eAbp(0).
Now we need to evaluate eAb, so we examine its Taylor expansion.
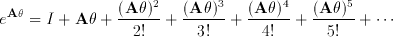
Considering how we constructed A, it is easy to verify that A^3 = -A Every additional application of A turns the plane of ppar aA^2 in the appropriate places, we get
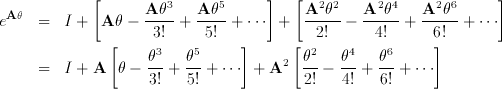
Now, we recognize the Taylor expansions for sin(b) and cos(b) in the above expression and find that
|