|
University of California, Berkeley EECS Dept, CS Division |
||
| Jordan Smith |
SLIDE: Scene Language for Interactive Dynamic Environments |
Prof. Carlo H. Séquin |
| Home | Goals | Publications | People | Gallery | Assignments | Distributions |
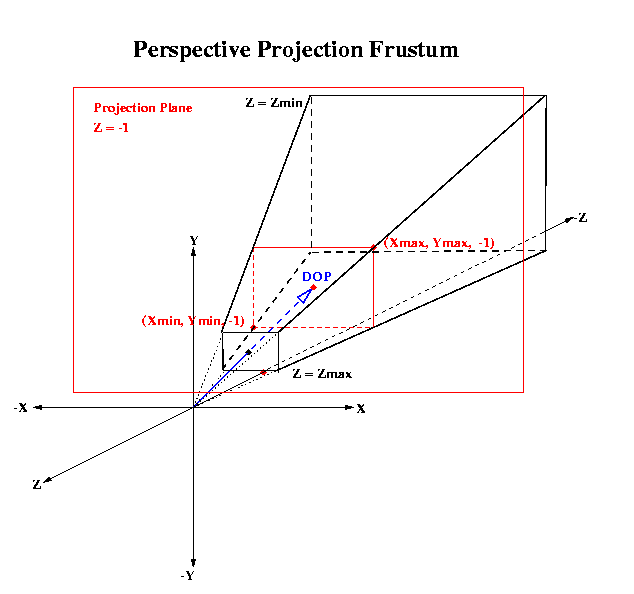
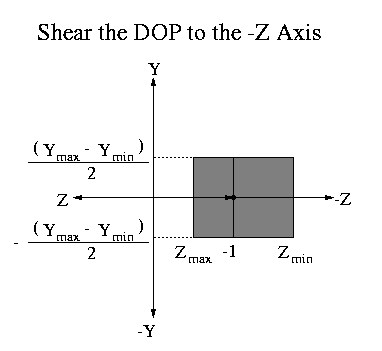
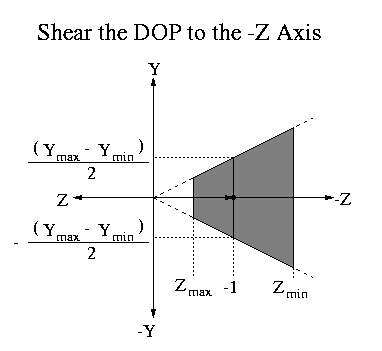
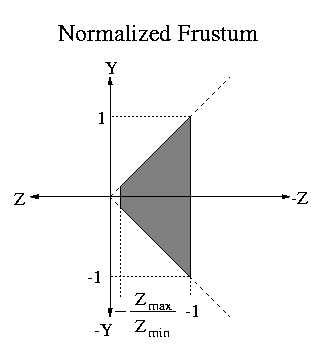
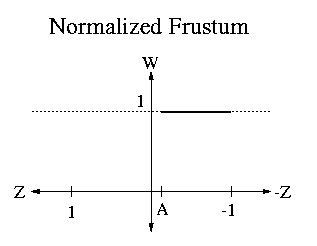
The figure below shows the SLIDE perspective viewing frustum in its
full generality, an off axis viewing window.

The transformation matrix that applies this perspective transformation is:
| Qwarp<-norm = |
|
| Qwarp<-norm-1 = |
|
You can download perspective.slf to your as6/SLIDE directory, or the new version perspective_new.slf. This is an interactive demo of what the perspective warp matrix is doing in a 2D perspective world ( Y Z W ). This example shows the homogeneous W = 1 plane sliced out of the 3D homogeneous space. You can animate the application of the perspective warp matrix and the application of the homogeneous division. You can also display the homogeneous clipping planes.
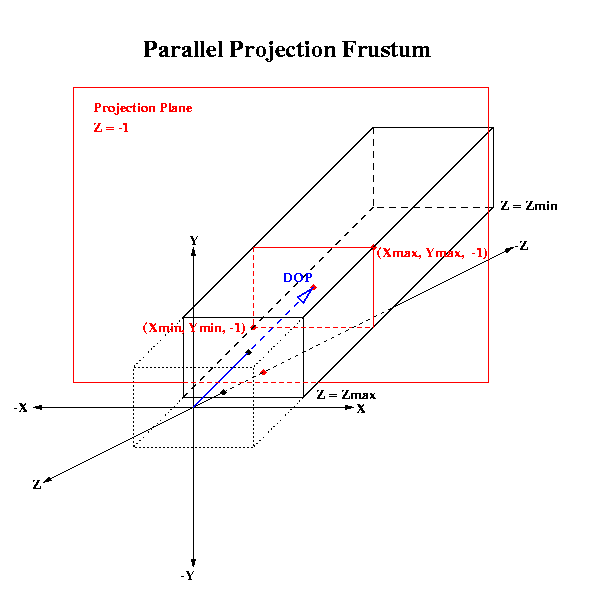
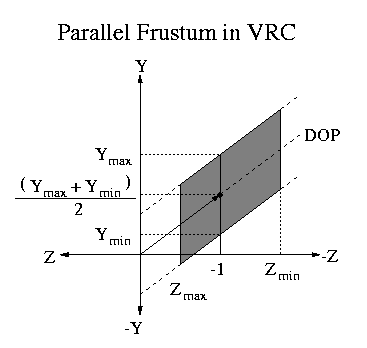
Parallel Projection |
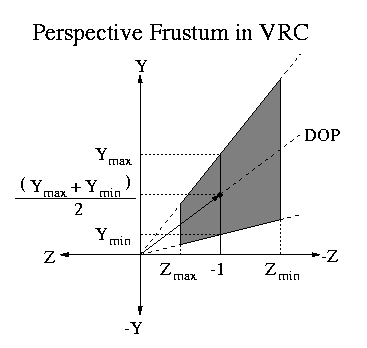
Perspective Projection |
|---|---|
 |
 |
 |
 |
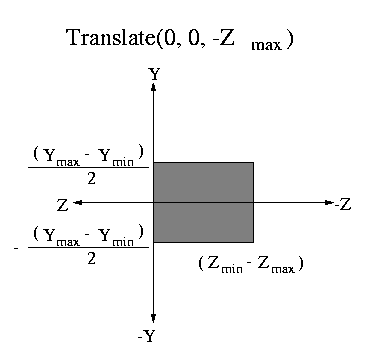 |
 |
 |
 |
Perspective Warp |
||
|---|---|---|
 |
 |
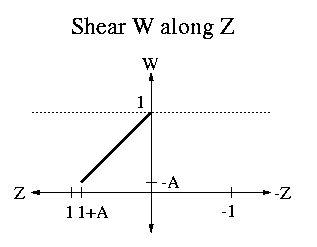 |
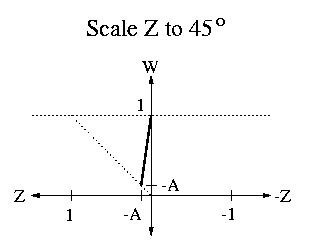 |
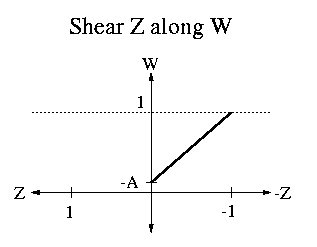 |
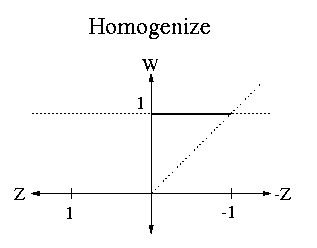 |
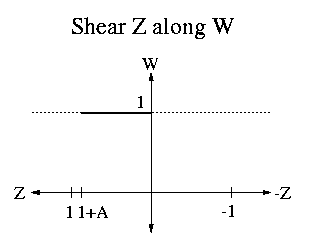
| Qwarp<-norm | = | SHz(-1) | * | Sz(-zfront/(1+zfront)) | * | SHw(-1) | * | SHz(1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
= |
|
* |
|
* |
|
* |
|
The problem is to find the intersection of a 4D line segment with one of the 4D clipping hyper-planes. This will be made easier because we are only dealing with special hyper-planes which contain the origin.
The parametric equation of a line in 4D is analogous to the parametric equation of a line in 3D. A line segment is defined by two 4D points p0 = [x0, y0, z0, w0] and p1 = [x1, y1, z1, w1]. The equation of the line through these points is then:
| L(t) | = | p0 + t * ( p1 - p0) | = |
|
t then has the range [0, 1] for the line segment.
The equation of a general hyper-plane in 4D is:
ax + by + cz + dw + e = 0But all the hyper-planes we will be dealing with contain the origin so e will always be 0. This simplifies the equation to:
ax + by + cz + dw = 0The clipping hyper-planes which we will be dealing with are:
| -w <= x <= w | -> | x = -w and x = w |
| -w <= y <= w | -> | y = -w and y = w |
| -w <= z <= 0 | -> | z = -w and z = 0 |
These clipping hyper-planes will also work for the parallel projection case because the w value will always be 1 under parallel projection. So, if we substitute w = 1 in the previous equations we get the following:
| -1 <= x <= 1 | -> | x = -1 and x = 1 |
| -1 <= y <= 1 | -> | y = -1 and y = 1 |
| -1 <= z <= 0 | -> | z = -1 and z = 0 |
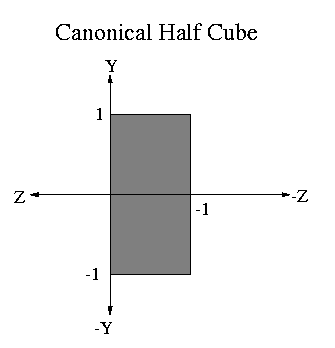
These are the same clipping planes we used to do the 3D clipping against the canonical half cube which we used in our parallel projection viewer.
We can generalize these six hyper-plane equations by the following short hand:
i = BB(i,j) * wWhere i is either is either x, y, or z.
And j is either min or max.
So BB(i,j) is one of the canonical half cube bounding box values:
| xmin | = | -1 |
| xmax | = | 1 |
| ymin | = | -1 |
| ymax | = | 1 |
| zmin | = | -1 |
| zmax | = | 0 |
If we then substitute the appropriate components from our line equation into our generalized hyper-plane equation, we get the following:
i0 + t*(i1 - i0) = BB(i,j) * ( w0 + t*(w1 - w0) )Solving for t we get the following expression:
t = ( (BB(i,j) * w0) - i0 ) / ( (i1 - i0) - (BB(i,j) * (w1 - w0)) )To make this a little more concrete, lets set i = x and j = max and then substitute in:
t = ( w0 - x0 ) / ( (x1 - x0) - (w1 - w0) )To verify that parallel projections will still work lets set all w's = 1:
t = ( BB(i,j) - i0 ) / (i1 - i0)To make this a little more concrete, lets set i = x and j = max and then substitute in:
t = ( 1 - x0 ) / (x1 - x0)
This page was originally built by Jordan Smith.
Last modified: Thursday, 07-Oct-2004 17:43:01 PDT