|
CS 189/289A
Introduction to Machine Learning
Jonathan
Shewchuk
Spring 2025
Mondays and Wednesdays, 6:30–8:00 pm
Wheeler Hall Auditorium (a.k.a. 150 Wheeler Hall)
Begins Wednesday, January 22
Discussion sections begin Tuesday, January 28
Contact:
Use Ed Discussion
for public and private questions that can be viewed by all the TAs.
I check Ed Discussion far more often and reliably than email.
For very personal issues, send email to
jrs@berkeley.edu.
My office hours:
Mondays, 5:10–6:00 pm, 510 Soda or 529 Soda,
Fridays, 5:10–6:00 pm, 510 Soda or 529 Soda,
and by appointment.
(I'm usually free after the lectures too.)
|
This class introduces algorithms for learning,
which constitute an important part of artificial intelligence.
Topics include
- classification: perceptrons, support vector machines (SVMs),
Gaussian discriminant analysis (including linear discriminant analysis,
LDA, and quadratic discriminant analysis, QDA), logistic regression,
decision trees, neural networks, convolutional neural networks,
boosting, nearest neighbor search;
- regression: least-squares linear regression, logistic regression,
polynomial regression, ridge regression, Lasso;
- density estimation: maximum likelihood estimation (MLE);
- dimensionality reduction: principal components analysis (PCA),
random projection; and
- clustering: k-means clustering, hierarchical clustering.
Useful Links
- Access the CS 189/289A
Ed Discussion
forum. If you haven't already been added to the class,
use this invitation link.
- Submit your assignments at the CS 189/289A
Gradescope.
If you need the entry code, find it on Ed Discussion in the
post entitled “Welcome to CS 189!”
- If you want an instructional account, you can
get one online.
Go to the same link if you forget your password or account name.
- Check out this
Machine Learning Visualizer by our former TA Sagnik Bhattacharya and
his teammates Colin Zhou, Komila Khamidova, and Aaron Sun.
It's a great way to build intuition for what decision boundaries different
classification algorithms find.
Prerequisites
- Math 54, Math 110, or EE 16A+16B (or another linear algebra course),
- CS 70, EECS 126, or Stat 134 (or another probability course),
- Math 53 (or another vector calculus course)—you need to understand
gradients and the multivariate chain rule, but not div or curl, and
- enough programming experience to be able to debug complicated programs
without much help. (Unlike in a lower-division programming course,
the Teaching Assistants are under no obligation to look at your code.)
You should take these prerequisites quite seriously.
If you don't have a solid intuitive understanding of linear algebra,
probability, and gradients, as well as substantial programming experience
with some attention to data structures,
I strongly recommend not taking CS 189.
However, the prerequisites are not formally enforced—rather,
they're enforced by the fact that you won't understand the class without them.
If you want to brush up on prerequisite material:
- There's a fantastic collection of linear algebra visualizations
on YouTube by
3Blue1Brown
(Grant Sanderson) starting with
this
playlist, The Essence of Linear Algebra.
I highly recommend them,
even if you think you already understand linear algebra.
It's not enough to know how to work with matrix algebra equations;
it's equally important to have a geometric intuition for
what it all means.
- Here's a
short summary of
math for machine learning written by our former TA Garrett Thomas.
- Stanford's machine learning class provides additional reviews of
linear algebra
and
probability
theory.
- To learn matrix calculus (which will rear its head first in Homework 2),
check out the first two chapters of
The
Matrix Cookbook.
- An alternative guide to CS 189 material
(if you're looking for a second set of lecture notes besides mine),
written by our former TAs Soroush Nasiriany and Garrett Thomas,
is available
at this link.
I recommend reading my notes first, but reading the same material
presented a different way can help you firm up your understanding.
Textbooks


Both textbooks for this class are available free online.
Hardcover and eTextbook versions are also available.
-
Gareth James,
Daniela Witten,
Trevor Hastie, and
Robert Tibshirani,
An
Introduction to Statistical Learning with Applications in R,
second edition, Springer, New York, 2021. ISBN # 978-1-0716-1417-4.
See Amazon for hardcover or eTextbook.
-
Trevor Hastie,
Robert Tibshirani, and
Jerome Friedman,
The Elements of Statistical Learning:
Data Mining, Inference, and Prediction, second edition,
Springer, 2008.
See Amazon for hardcover or eTextbook.

Homework and
Exams
You have a total of 5 slip days that you can apply to your
semester's homework.
We will simply not award points for any late homework you submit that
would bring your total slip days over five.
If you are in the Disabled Students' Program and you are offered an extension,
even with your extension plus slip days combined,
no single assignment can be extended more than 5 days.
(We have to grade them sometime!)
The following homework due dates are tentative and may change.
Homework 1
is due Wednesday, January 29 at 11:59 PM.
(Warning: 16 MB zipfile.
Here's just the written part.)
Homework 2
is due Wednesday, February 12 at 11:59 PM.
(PDF file only.)
Homework 3
is due Wednesday, February 26 at 11:59 PM.
(Warning: 15 MB zipfile.
Here's just the written part.)
Homework 4
is due Wednesday, March 12 at 11:59 PM.
Instead of serving a zipfile from here, the data and a helper script are
available from
the
Kaggle link.
Homework 5
is due Thursday, April 3 at 11:59 PM.
(Here's just the written part.)
Homework 6
is due Friday, April 25 at 11:59 PM.
(Warning: 140 MB zipfile.
Here's just the written part.)
Homework 7
is due Wednesday, May 7 at 11:59 PM.
(Warning: 112 MB zipfile.
Here's just the written part.)
The CS 289A Project
has a proposal due Friday, April 11.
The video is due Monday, May 12, and
the final report is due Tuesday, May 13.
The Midterm took place on
Monday, March 17 at 7:00–9:00 PM in multiple rooms on campus.
Previous midterms are available:
Without solutions:
Spring 2013,
Spring 2014,
Spring 2015,
Fall 2015,
Spring 2016,
Spring 2017,
Spring 2019,
Summer 2019,
Spring 2020 Midterm A,
Spring 2020 Midterm B,
Spring 2021,
Spring 2022,
Spring 2023,
Spring 2024,
Spring 2025.
With solutions:
Spring 2013,
Spring 2014,
Spring 2015,
Fall 2015,
Spring 2016,
Spring 2017,
Spring 2019,
Summer 2019,
Spring 2020 Midterm A,
Spring 2020 Midterm B,
Spring 2021,
Spring 2022,
Spring 2023,
Spring 2024,
Spring 2025.
The Final Exam will take place on Friday, May 16 at 3–6 PM
in a place to be determined.
Previous final exams are available.
Without solutions:
Spring 2013,
Spring 2014,
Spring 2015,
Fall 2015,
Spring 2016,
Spring 2017,
Spring 2019,
Spring 2020,
Spring 2021,
Spring 2022,
Spring 2023,
Spring 2024,
Spring 2025.
With solutions:
Spring 2013,
Spring 2014,
Spring 2015,
Fall 2015,
Spring 2016,
Spring 2017,
Spring 2019,
Spring 2020,
Spring 2021,
Spring 2022,
Spring 2023,
Spring 2024,
Spring 2025.
Lectures
Now available:
The complete
semester's lecture notes (with table of contents and introduction).
Lecture 1 (January 22):
Introduction.
Classification.
Training, validation, and testing.
Overfitting and underfitting.
Read ESL, Chapter 1.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 2 (January 27):
Linear classifiers.
Decision functions and decision boundaries.
The centroid method.
Perceptrons.
Read parts of the Wikipedia
Perceptron page.
Optional: Read ESL, Section 4.5–4.5.1.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 3 (January 29):
Gradient descent, stochastic gradient descent, and
the perceptron learning algorithm.
Feature space versus weight space.
The maximum margin classifier, aka hard-margin support vector machine (SVM).
Read ISL, Section 9–9.1.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 4 (February 3):
The support vector classifier, aka soft-margin support vector machine (SVM).
Features and nonlinear decision boundaries.
Read ESL, Section 12.2 up to and including the first paragraph of 12.2.1.
Optional: check out this
short visualization
of the parabolic lifting map.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 5 (February 5):
Machine learning abstractions: application/data, model,
optimization problem, optimization algorithm.
Common types of optimization problems:
unconstrained, linear programs, quadratic programs.
The influence of the step size on gradient descent.
Optional: Read (selectively) the Wikipedia page on
mathematical
optimization.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 6 (February 10):
Decision theory, also known as risk minimization:
the Bayes decision rule and the Bayes risk.
Generative and discriminative models.
Read ISL, Section 4.4 (the first few pages).
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 7 (February 12):
Gaussian discriminant analysis, including
quadratic discriminant analysis (QDA) and linear discriminant analysis (LDA).
Maximum likelihood estimation (MLE) of the parameters of a statistical model.
Fitting an isotropic Gaussian distribution to sample points.
Read ISL, Section 4.4 (all of it).
Optional: Read (selectively) the Wikipedia page on
maximum
likelihood estimation.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
February 17 is Presidents' Day.
Lecture 8 (February 19):
Eigenvectors, eigenvalues, and the eigendecomposition of
a symmetric real matrix.
The quadratic form and ellipsoidal isosurfaces as
an intuitive way of understanding symmetric matrices.
Application to anisotropic multivariate normal distributions.
The covariance of random variables.
Read Chuong Do's
notes on the multivariate Gaussian distribution.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 9 (February 24):
MLE, QDA, and LDA revisited for anisotropic Gaussians.
Read ISL, Sections 4.4 and 4.5.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 10 (February 26):
Regression: fitting curves to data.
The 3-choice menu of regression function + loss function + cost function.
Least-squares linear regression as quadratic minimization.
The design matrix, the normal equations, the pseudoinverse, and
the hat matrix (projection matrix).
Logistic regression; how to compute it with gradient descent or
stochastic gradient descent.
Read ISL, Sections 4–4.3.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 11 (March 3):
Newton's method and its application to logistic regression.
LDA vs. logistic regression: advantages and disadvantages.
ROC curves.
Weighted least-squares regression.
Least-squares polynomial regression.
Read ISL, Sections 7.1, 9.3.3; ESL, Section 4.4.1.
Optional: here is
a
fine short discussion of ROC curves—but skip the incoherent question
at the top and jump straight to the answer.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 12 (March 5):
Statistical justifications for regression.
The empirical distribution and empirical risk.
How the principle of maximum likelihood motivates the cost functions for
least-squares linear regression and logistic regression.
The bias-variance decomposition;
its relationship to underfitting and overfitting;
its application to least-squares linear regression.
Read ESL, Sections 2.6 and 2.9.
Optional: Read the Wikipedia page on
the
bias-variance trade-off.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
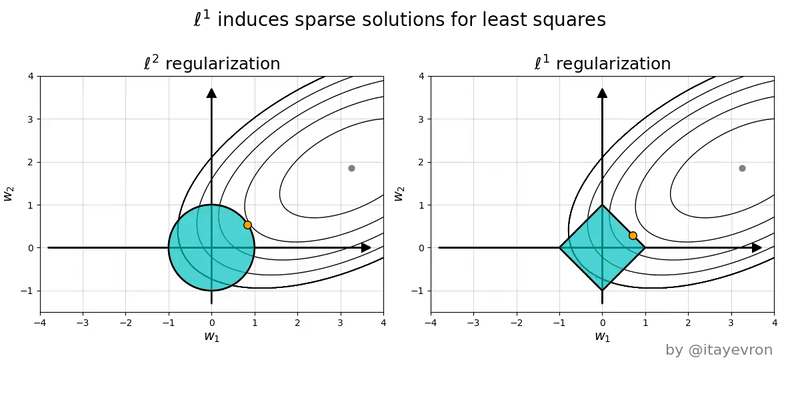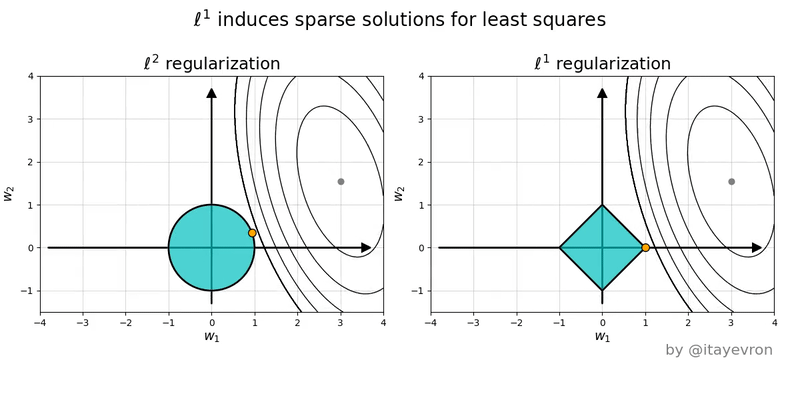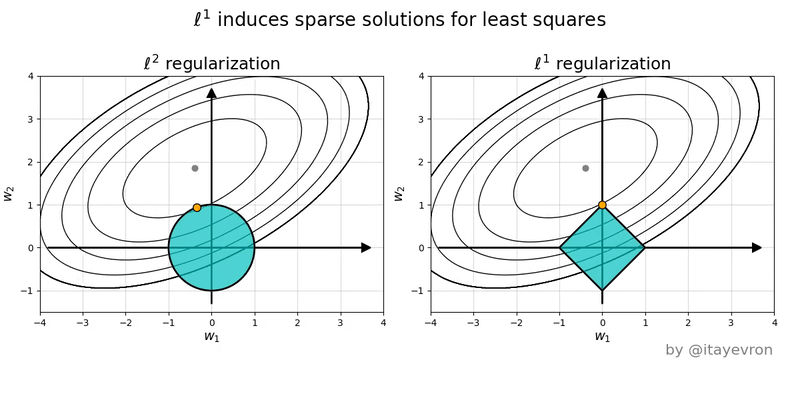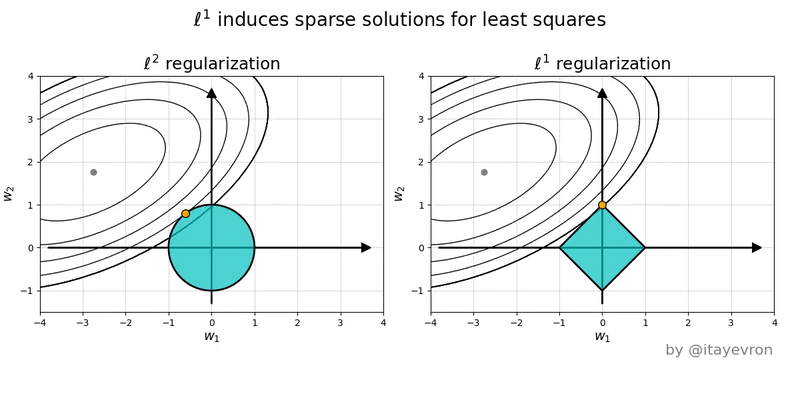
Lecture 13 (March 10):
Ridge regression: penalized least-squares regression for reduced overfitting.
How the principle of maximum a posteriori (MAP) motivates
the penalty term (aka Tikhonov regularization).
Subset selection.
Lasso: penalized least-squares regression for reduced overfitting and
subset selection.
Read ISL, Sections 6–6.1.2, the last part of 6.1.3 on validation,
and 6.2–6.2.1; and ESL, Sections 3.4–3.4.3.
Optional: This CrossValidated page on
ridge
regression is pretty interesting.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 14 (March 12):
Decision trees; algorithms for building them.
Entropy and information gain.
Read ISL, Sections 8–8.1.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
The Midterm took place
Monday, March 17 at 7:00–9:00 PM.
The midterm covers Lectures 1–13,
the associated readings listed on the class web page, Homeworks 1–4, and
discussion sections related to those topics.
Lecture 15 (March 19):
More decision trees: decision tree regression;
stopping early; pruning; multivariate splits.
Ensemble learning, bagging (bootstrap aggregating), and random forests.
Read ISL, Section 8.2.
Optional: An interesting discussion about how
ensemble learning won the Netflix Prize appeared in Wired Magazine:
Eliot
Van Buskirk, “BellKor's Pragmatic Chaos Wins $1 Million Netflix Prize by
Mere Minutes”.
The animations I show in class are available
in
this directory.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
March 24–28 is Spring Recess.
Lecture 16 (March 31):
Neural networks.
Gradient descent and the backpropagation algorithm.
Read Bishop, Sections 8–8.1.3 and 8.1.5.
Optional: Welch Labs' video tutorial
Neural
Networks Demystified on YouTube is quite good
(note that they transpose some of the matrices from our representation).
Also of special interest is this Javascript
neural net demo
that runs in your browser.
Here's
another
derivation of backpropagation that some people have found helpful.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 17 (April 2):
The vanishing gradient problem.
Rectified linear units (ReLUs).
Backpropagation with softmax outputs and cross-entropy loss.
Differences between traditional computational models and
neuronal computational models.
Read Bishop, Sections 6.2.3 and 6.4.
Optional: Try out some of the Javascript demos on
this
excellent web page—and if time permits, read the text too.
The first four demos illustrate the neuron saturation problem and
its fix with the logistic loss (cross-entropy) functions.
The fifth demo gives you sliders so you can understand how softmax works.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 18 (April 7):
Neuron biology: axons, dendrites, synapses, action potentials.
Heuristics for faster training.
Read Bishop, Sections 7.2.3–7.2.5 and 7.3.1–7.4.1.
Optional: A fine paper on heuristics for better neural network learning is
Yann LeCun,
Léon Bottou, Genevieve B. Orr, and Klaus-Robert Müller,
“Efficient BackProp,” in G. Orr and K.-R. Müller (Eds.),
Neural Networks: Tricks of the Trade, Springer, 1998.
The advice on weight initialization comes from Siddharth Krishna Kumar,
On Weight Initialization in
Deep Neural Networks, arXiv abs/1704.08863, May 2017.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 19 (April 9):
Convolutional neural networks.
Neurology of retinal ganglion cells in the eye and
simple and complex cells in the V1 visual cortex.
Read Bishop, Sections 10.2–10.3.2.
Optional:
LeNet 5 was introduced by
Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner,
Gradient-Based
Learning Applied to Document Recognition,
Proceedings of the IEEE 86(11):2278–2324, 1998.
AlexNet was introduced by Alex Krizhevsky, Ilya Sutskever, and
Geoffrey E. Hinton,
ImageNet
Classification with Deep Convolutional Neural Networks,
Advances in Neural Information Processing Systems 25
(F. Pereira, C. J. Burges, L. Bottou, and K. Q. Weinberger, editors),
December 2012.
The images from the deeper layers of the convolutional network come from
Matthew D. Zeiler and Rob Fergus,
Visualizing and Understanding
Convolutional Networks,
Computer Vision—European Conference on Computer Vision 2014,
Lecture Notes in Computer Science volume 8689, pages 818-833, Springer Nature,
September 2014.
Here is the video about
Hubel and Wiesel's experiments on the feline V1 visual cortex.
Here is Yann LeCun's video demonstrating LeNet5.
Of special interest is this Javascript
convolutional
neural net demo that runs in your browser.
Some slides about the V1 visual cortex and ConvNets
(PDF).
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 20 (April 14):
Unsupervised learning.
Principal components analysis (PCA).
Derivations from maximum likelihood estimation, maximizing the variance, and
minimizing the sum of squared projection errors.
Eigenfaces for face recognition.
Read ISL, Sections 12–12.2
(if you have the first edition, Sections 10–10.2) and
the Wikipedia page on
Eigenface.
Optional:
Watch
the video for Volker Blanz and Thomas Vetter's
A Morphable Model for the Synthesis of 3D Faces.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 21 (April 16):
The singular value decomposition (SVD) and its application to PCA.
Clustering: k-means clustering aka Lloyd's algorithm;
hierarchical clustering; greedy agglomerative clustering.
Dendrograms.
Read ISL, Section 12.4 (if you have the first edition, Section 10.3).
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 22 (April 21):
The pseudoinverse and its relationship to the singular value decomposition.
Better generalization for neural networks:
data augmentation, l2 regularization, dropout, double descent.
Read Bishop, Sections 9.2, 9.3.2, and 9.6.
Optional: Dropout was introduced by
G. E. Hinton, N. Srivastava, A. Krizhevsky, I. Sutskever, and
R. R. Salakhutdinov,
Improving Neural Networks by
Preventing Co-adaptation of Feature Detectors, arXiv abs/1207.0580,
2012.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 23 (April 23):
Batch normalization.
Residual neural networks (“ResNets”).
Accelerated descent with AdamW
(“adaptive moment estimation with weight decay”).
Read Bishop, Sections 7.4.2, 7.4.3, and 9.5.
Optional: batch normalization was introduced by
Sergey Ioffe and Christian Szegedy,
Batch Normalization:
Accelerating Deep Network Training by Reducing Internal Covariate Shift,
Proceedings of the 32nd International Conference on Machine Learning
(Lille, France), 2015.
Layer normalization was introduced by
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E. Hinton,
Layer Normalization,
arXiv abs/1607.06450, July 2016.
Sergey Ioffe and Christian Szegedy,
Residual neural networks were introduced by
Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun,
Deep Residual Learning for
Image Recognition,
2016 IEEE Conference on Computer Vision and Pattern Recognition
(Las Vegas, Nevada), June 2016.
But I suggest reading their follow-up paper first:
Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun,
Identity Mappings in
Deep Residual Networks,
Computer Vision—European Conference on Computer Vision 2016,
Lecture Notes in Computer Science volume 9908, pages 630-645, Springer Nature,
October 2016.
The ConvNeXt residual neural network comes from
Zhuang Liu, Hanzi Mao, Chao-Yuan Wu, Christoph Feichtenhofer, Trevor Darrell,
and Saining Xie,
A ConvNet for the 2020s,
2022 Conference on Computer Vision and Pattern Recognition
(New Orleans, Louisiana), June 2022.
Adam was introduced by Diederik P. Kingma and Jimmy Lei Ba,
Adam: A Method for
Stochastic Optimization,
Third International Conference for Learning Representations
(San Diego, California), May 2015.
AdamW was introduced by Ilya Loshchilov and Frank Hutter,
Decoupled Weight Decay
Regularization, arXiv abs/1711.05101, 2019.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 24 (April 28):
AdaBoost, a boosting method for ensemble learning.
Nearest neighbor classification and its relationship to the Bayes risk.
Read ESL, Sections 10–10.5, and ISL, Section 2.2.3.
For reference: Yoav Freund and Robert E. Schapire,
A Decision-Theoretic
Generalization of On-Line Learning and an Application to Boosting,
Journal of Computer and System Sciences 55(1):119–139,
August 1997.
Freund and Schapire's
Gödel
Prize citation and their
ACM
Paris Kanellakis Theory and Practice Award citation.
For reference: Thomas M. Cover and Peter E. Hart,
Nearest
Neighbor Pattern Classification,
IEEE Transactions on Information Theory 13(1):21–27,
January 1967.
For reference: Evelyn Fix and J. L. Hodges Jr.,
Discriminatory
Analysis---Nonparametric Discrimination: Consistency Properties,
Report Number 4, Project Number 21-49-004,
US Air Force School of Aviation Medicine, Randolph Field, Texas,
1951.
See also This commentary
on the Fix–Hodges paper.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
Lecture 25 (April 30):
The exhaustive algorithm for k-nearest neighbor queries.
Speeding up nearest neighbor queries.
Voronoi diagrams and point location.
k-d trees.
If I like machine learning, what other classes should I take?
For reference:
the best paper I know about how to implement a k-d tree is
Sunil Arya and David M. Mount,
Algorithms for
Fast Vector Quantization,
Data Compression Conference, pages 381–390, March 1993.
For reference:
the IM2GPS web page,
which includes a link to the paper.
My lecture notes (PDF).
The lecture video.
In case you don't have access to bCourses, here's
a
backup screencast (screen only).
The Final Exam
will take place on Friday, May 16 at 3–6 PM
Discussion
Sections and Teaching Assistants
Discussion sections are listed in this calendar.
Your Teaching Assistants are:
Suchir Agarwal
Circle Chen
SooHyuk Cho
Margarita Geleta
Ayush Goel
Owen Gozali
Grace Luo
Rami Mrad
James Ni
Sara Pohland
Tejas Prabhune
Royce Ren
Yide Shentu
Bill Zheng
Grading
-
40% for homeworks.
-
20% for the Midterm.
-
CS 189: 40% for the Final Exam.
-
CS 289A: 20% for the Final Exam.
-
CS 289A: 20% for a Project.
Supported in part by the National Science Foundation under
Awards CCF-0430065, CCF-0635381, IIS-0915462, CCF-1423560, and CCF-1909204,
in part by a gift from the Okawa Foundation,
and in part by an Alfred P. Sloan Research Fellowship.

This illustration is copyright 2023 by Jason Diwa
|





