CS 285: SOLID MODELING

Lecture #8 -- Monday, Sept. 26, 2011

PREVIOUS < - - - - > CS 285 HOME < - - - - > CURRENT < - - - - > NEXT

Warmup Question:

Suppose you have designed a nice mathematical surface to represent your bell
(e.g., a Gaussian bell-shaped hump).

How can you now turn this 2-manifold into a thicker surface
so that this object can be physically realized?

Discuss tentative bell designs -- any problems ?

Show: a bell by Steve Reinmuth (more bells)

Some innovative designs:

Andrew Brandon Ayden

Offset Curves

Outside and inside curves at a given distance to a given 2D shape.

For polygonal shapes, true offset curves are composed of straight line segments and circular arcs.

Mitered approximations can be calculated by increasing the offset as 1/cos(alfa); where alfa is half the dihedral angle.

OffsetSurfaces

Locus of all points at a given distance (outside and inside) from a given 2-manifold.

For polyhedral shapes, offset surfaces are composed of planar facets, cylinder segments, and pieces of spheres.

Mitered approximations can be calculated by letting the offset facets extend and intersect with their neighbors; however, more than three facet may intersect in more then one vertex. If the original dihedral angles are not too extreme, we can fudge an approximate offset surface by just calculating new offset vertices and connecting them in the same way that the original vertices were connected. The offset distcance might be stretched with an averaged 1/cos(alfa).

Offset Surfaces Implemented in SLIDE:

First all geometry is merged in a hierarchically flat mesh of connected facets.
Simply polyhedral offset surfaces (inside and outside) are then created by calculating offset vertex locations.
Each original facet results in two new facets; the two offset surfaces are connected along their rims with additional edge-facets.
The offset algorithm does not handle self-intersections or topology changes.

Two offset types are available:

`SLF_OFFSET_ANGULAR`		This offsets the control mesh inward and outward. Each facet in the control mesh will map to two facets in the offset mesh. Each boundary edge will map to a quadrilateral. The control mesh does not have to be a closed polyhedron.
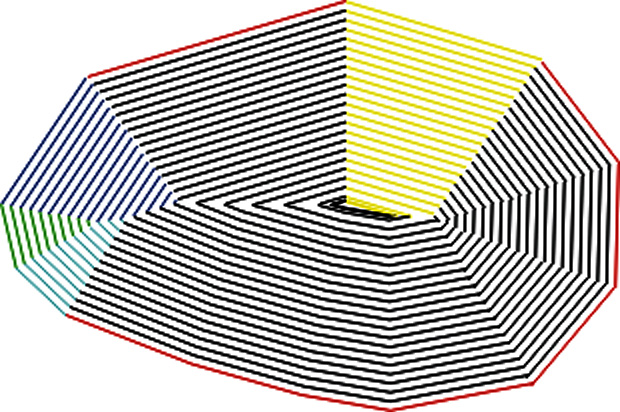
`SLF_OFFSET_PERFORATED`		In this offsetting technique, the edges of the control mesh are viewed as infinitely thin wires which are then thickened in an angular way. The control mesh does not have to be a closed polyhedron.

SLF_OFFSET_ROUNDED This has not been implemented.

Two SLIDE demo programs:

cube_subdiv_offset.slf
A simple demo on a subdivision net generated from 3 cube faces.

Offset_tube.slf
A simple demo on a piece of elliptical tubing following a circular arc.

Paper Presentations

How to efficiently and effectively read a paper to prepare for in-class discussions:

Read: "Introduction," "Conclusions;" look at Figures and read captions.
This should typically tell you WHAT the authors have done, and WHY.
Now try to find out HOW they did it:
Look for the appropriate sections that describe the key techniques.
Also try to get an understanding what the limitations and caveats are of the described approach.
Might there be things that the authors do NOT tell you ?
You can probably skip the section on "Previous Work" or just skim it.
Write down a few of the key points you learned,
as well as some questions that are good for discussion in class.

Reading Assignment for Wed 9/28:

DF00: Frisken et.al.: "Adaptively Sampled Distance Fields"

Continuing Homework Assignment#5:

Modeling with SLIDE -- and (later) building it on the FDM!

Due: First draft: Monday, 9/26/2011: 4pm
Final Design: Wednesday, 9/28.2011: 10am