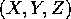 . Assume that the camera
moves with translational velocity
. Assume that the camera
moves with translational velocity 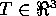 and the
angular velocity
and the
angular velocity  and
the observed scene is stationary (see
Figure 5). This is referred to as egomotion.
and
the observed scene is stationary (see
Figure 5). This is referred to as egomotion.
Now we want to relate the motion of the camera frame to the optical flow
pattern which it generates. For simplicity we will concentrate again only
on a single point with 3-D coordinates 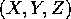 . Assume that the camera
moves with translational velocity
. Assume that the camera
moves with translational velocity 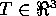 and the
angular velocity
and the
angular velocity  and
the observed scene is stationary (see
Figure 5). This is referred to as egomotion.
and
the observed scene is stationary (see
Figure 5). This is referred to as egomotion.

Figure 5: Showing the motion of the camera relative to a point.
By differentiating the equation for a projective transformation, we find that the optical flow of a point caused by the motion of the camera is:
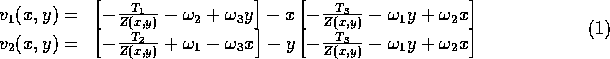
where  gives the coordinates of the scene point corresponding
to the image at
gives the coordinates of the scene point corresponding
to the image at 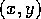 . This equation is complicated, but can be
understood better for the case of pure translation, that is,
. This equation is complicated, but can be
understood better for the case of pure translation, that is,  , in which case the flow field becomes:
, in which case the flow field becomes:
It is of interest to note that 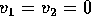 at the point
at the point  . This point is called the focus of
expansion. Using this, as the origin, that is defining
. This point is called the focus of
expansion. Using this, as the origin, that is defining  , it follows that
, it follows that
The useful thing about this equation (3 is that it enables us to
determine the time to impact with an object at a distance  ,
away given by
,
away given by 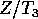 . You can imagine that this is important for
navigation and also your well being.
. You can imagine that this is important for
navigation and also your well being.
Another use of motion flow is in rendering . Here you take multiple 2-D views of a fixed scene and use it to reconstruct the 3-D shape of the object. An example of this is given in Figure (6).

Figure 6: 3-D reconstruction of a house from four photographs taken
from different locations (left) and the photograph of the house taken
from the same location (right). Figure taken from Russell and Norvig,
``Artificial Intelligence - A Modern Approach, Prentice Hall, 1995,
Figure 24.11, page 738
Fancier versions of this are due to Debevec, Taylor and Malik and are available here.