I am currently a Research Scientist in the computer science department at University of California, Berkeley.
In recent years, my research has turned to questions in the field of Quantum Hamiltonian Complexity. The questions I consider sit at the intersection of mathematics, computer science, and condensed matter physics with the quest of understanding the structure and complexity of many body physical systems. A nice brief description of the field can be found here.
In addition to this current interest in quantum computation, past research has focussed on questions in the fields of operator theory and signal processing, and Von Neumann algebras and subfactor theory. The questions I consider in these three areas share the common attribute that their underlying structure is determined by linear operators and the interplay and structure of collections of these operators. Collectively, this research is connected to a wide range of mathematical fields: computational complexity theory, statistical mechanics, signal, image and data processing, sampling theory, subfactor theory, C* algebras, low dimensional topology, quantum field theory.
Included below are brief and incomplete descriptions of the three areas highlighted above. They are meant to give an impression of the areas related to my interests. A list of my publications can be found here.
Quantum Hamiltonian Complexity.
Quantum Computation
At the core of any computational device is the use and control of physical phenomena. In this way the scale makes use of the physics of gravity, the manual cash register makes use of the physics of mechanics, and the modern computer makes use of the physics of electricity. The advances in the understanding of quantum phenomena has led to various notions of a quantum computer: a computational device that makes use of the physics of quantum mechanics.
In recent years, the theoretical study of quantum systems serving as computational devices has greatly advanced. These advances show that quantum computers, if built, could be used as powerful computational tools, able to perform tasks that classical computers are unable to do. The most notable of these algorithmic advances are the ability to search databases of size n in the square root of n steps and the ability to factor numbers in polynomial time. This later result sparked a very large interest in quantum computation for two reasons: 1) it showed that the RSA cryptosystem could be broken by a quantum computer, 2) it showed that a problem that is widely thought to not be in classical P is solvable for a quantum computer in polynomial time. Since these advances, though steady progress and understanding of the power of quantum computation has been made, no new groundbreaking algorithms have been found.
I'm interested in understanding the full power of quantum computation, both by designing new quantum algorithms and by describing the limits of the computational power of a quantum computer.
Quantum Hamiltonian Complexity
The original vision of a quantum computer, introduced by Feynman, was not a device for solving classical problems but rather a device for simulating many body quantum systems. From this lens, the motivating questions become the structure and complexity of many-body systems, an area known as Quantum Hamiltonian Complexity. For problems in this area techniques and ideas from mathematics, computer science, and condensed matter physics all apply.
Much of my recent research has been related to a well known conjecture that says that the complexity of natural many body systems satisfy a so called area law : that the entropy of a system between two regions scales as a function of the surface area between the systems rather than the volume of the areas. Though widely believed to hold in some form for a long time, there is no proof of the area law for 2 or 3 dimensional systems. M. Hastings proved the area law for gapped 1 dimensional systems in 2007. The work here provides an exponential improvement on Hastings' parameters for the area law of 1 dimensional systems, while the work here gives a polynomial time classical algorithm for computing ground states of gapped 1 dimensional systems.
Operator theory and signal processing
A collection of functions {fn}, indexed by the integers, is called a frame if there exist constants A, B>0 with
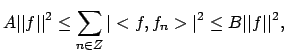
for all f in H. The notion of a frame is a generalization of a notion of a basis in that the constants A and B ensure that {fn} has enough elements to span H and yet does not have too much redundancy. Indeed, a frame always has a dual frame {f'n} so that
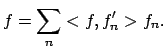
The essential advantage of frames is the overcomplete or redundant aspect of their structure. This can be exploited in two ways: a) to provide a more robust expansion of a vector so as to make it reconstructable even if some of the coefficients are lost or subject to noise, b) to provide a more compact expansion of a subset of vectors coming from a common source (i.e. images, audio) by choosing the frame elements to model essential features of the source. For these reasons, the theory of frames for a Hilbert space plays a fundamental role in signal processing, image processing, data compression and sampling theory.
The connection of frames with operator theory is made apparent by the existence of a canonical bounded linear operator that maps an orthonormal basis indexed by the integers onto the frame {fn}. Various properties of this canonical operator such as its range, inverse, and spectrum can be used to analyze the frame.
I'm interested in understanding the structure of the overcompleteness of frames with the ultimate goal of classifying, comparing, and designing frames.
Von Neumann algebras, subfactor theory, and planar algebras.
Von Neumann algebras are algebras M of operators on a Hilbert space H closed in the strong topology. The double commutant theorem of von Neumann shows that these algebras can be alternately described algebraically as algebras that are their own double commutant: that is, M where M' , the commutant of M,, is the collection of all bounded operators that commute with all the operators of M . This dual characterization, one analytic and one algebraic is at the heart of the rich structure and broad influence that the study of von Neumann algebras has produced. A factor is a von Neumann algebra M with a trivial center: M intersect M' equalling the scalars . All von Neumann algebras can be realized as a direct sum (or a direct integral) of factors and thus the study of von Neumann algebras can be refined to the study of factors.
Given an inclusion N inside M of type II-1 factors with finite index, V. Jones has given a canonical construction that produces a lattice of finite dimensional algebras known as the standard invariant. Work by S. Popa has shown that under certain conditions the standard invariant is a complete invariant, and thus a very important structure within the study of subfactors. The simplest standard invariant is the Temperley-Lieb algebra and is an underlying symmetry of the standard invariant of any subfactor. (The Temperley-Lieb algebra is a representation of the braid group. It is used to generate the Jones polynomial invariant for knots.)
S. Popa provided an abstract algebraic characterization of the standard invariant called a lambda-lattice. Subsequently Jones developed an equivalence between lambda-lattices and objects he termed planar algebras. In the planar algebra framework, many of the seemingly complicated algebraic conditions associated with a lambda-lattice can be simply described in terms of the geometry of the plane.
The planar algebra paradigm has opened up a new point of view for the study of subfactors which has led to a significant body of new results and ideas. I'm interested in continuing to explore this new point of view.