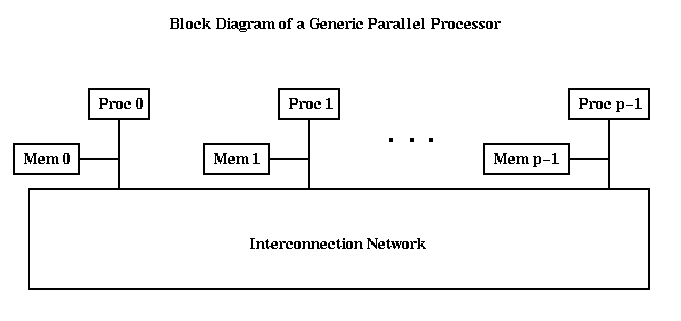

There are p processors, numbered from Proc 0 to Proc p-1, each of which has a memory, and all of which communicate over some Interprocessor Communication Network. We need to make a few simple distinctions among architectures of this form, the first of which is Flynn's taxonomy:
All the computers we will use this semester, and most parallel computers used for general computing, are MIMD. MIMD machines can clearly support a superset of the operations performed by an SIMD machine. SIMD computers were built historically because they were simpler to design and program, and can still be cost-effective for special applications (such as systolic arrays for digital signal processing). A recent SIMD machine is the CM-2 (predecessor of the MIMD CM-5), and the MasPar is currently on the market. However, in order to exploit fast, cheap commodity microprocessors, most machines are MIMD. SIMD machines did inspired a programming style, called data parallel programming, which remains popular; two instantiations are Connection Machine Fortran (CMF) and High Performance Fortran (HPF).The second distinction among parallel architectures we wish to make is to categorize MIMD machines as Distributed Address Space or Shared Address Space. The issues is whether a processor can "see" only part of the total memory of the machine, or all of it. In other words, when a Proc i issues a "load memory location k into Register 1" instruction, the question is whether location k can refer only to a location in Mem i (Distributed Address Space), or whether it can refer to any location in any other Mem j (Shared Address Space). From the point of view of Proc i, Mem i is called local memory, and any other Mem j is called remote memory. The CM-5, the IBM SP-1 and any current network of workstations are all distributed memory machines. The Cray C90 with more than 1 processor, and "symmetric multiprocessors" produced by SUN and SGI are shared memory machines.
Clearly, a Shared Address Space machine is more powerful than a Distributed Address Space machine, in the sense that the former can address a superset of the locations of the latter. As we will see, a Shared Address Space also makes certain programming problems much easier. In fact, this has led to programming styles which are attempt to simulate shared memory using distributed memory (Split-C, as described later).
These distinctions among architectures are imprecise, because in principle any MIMD machine can simulate any other MIMD machine using software, though the performance may be poor.
These languages roughly correspond to the architectural models just discussed:
I say roughly, because any of these languages may be implemented on any MIMD machine, perhaps with some operations, such as accesses of memory simulated in software. In other words, as an applications programmer using an MIMD machine, you might choose to use any of these languages for your problem. Whether or not you get good performance from your choice is something we will have to consider later. For now, we concentrate on the expressive power of each kind of parallel language.To organize our presentation of each language, we will ask the following questions:
Let us compare the Matlab and CMF solution of the first Sharks and Fish problem, fish swimming in a current. (You should pop up the source code for these two programs in separate windows.) As you can see, they are quite similar.
For example, the statement
fishp = fishp + dt * fishv
in both programs means to multiply the array of fish velocities, fishv,
by the time step dt, to add it to the array of fish positions, fishp,
and replace fishp by its new value. The arrays must be conformable,
i.e. have the same size and shape, in order to be operated on together in
this way. The sequential equivalent of this would be
for i = 1 to nfish (number of fish)
fishp(i) = fishp(i) + dt*fishv(i)
end
The CMF compiler will automatically assume that array operation are
to be done in parallel, provided the arrays are declared to reside
on more than one processor, as we explain below.
Continuing our comparison of the codes, consider the updating of the mean square velocity
Matlab: mnsqvel = [mnsqvel,sqrt(sum(abs(fishv).^2)/length(fishp))];
CMF : fishspeed = abs(fishv)
mnsqvel = sqrt(sum(fishspeed*fishspeed)/nfish)
We ignore the fact that mnsqvel is a scalar in CMF and an array in Matlab,
and concentrate on the computation on the right-hand-side. In both
cases, the intrinsic function abs() is applied to a whole array fishv,
and then the array elements are summed by the intrinsic function sum(),
which reduces to a scalar. Operations like sum(), prod(), max(), min()
are called reduction operations because the reduce arrays to scalars.
Now we compare the subroutines, both called current, which compute the current at each fish position. The Matlab solution uses a function which takes an array argument (fishp), and returns an array result (the force on each fish), whereas the CMF solution uses a subroutine which has on input array argument, (fishp), and one output array argument (force).
Matlab: X = fishp*sqrt(-1);
X = 3*X ./ max(abs(X),.01) - fishp;
CMF : force = (3,0)*(fishp*ii)/(max(abs(fishp),0.01)) - fishp
This illustrates the use of the intrinsic abs(), reduction operator
max(), with a scalar argument and array argument, and various array operations.
Graphics is handled in different ways by the two systems. CMF uses a 256-by-256 integer array "show" to indicate the presense or absence of fish in a window -zoom <= x,y <= zoom. Each fish position is appropriately scaled to form an integer array x of x-coordinates in the range from 1 to 256, and and integer array y of y-coordinates in the range from 1 to 256, after which only corresponding entries of "show" are set to one. This is done using the parallel construct "for all":
x = INT(( real(fishp)+zoom)/(zoom)*(m/2))
y = INT((aimag(fishp)+zoom)/(zoom)*(m/2))
show = 0
forall(j=1:nfish) show(x(j),y(j)) = 1
Note that we must have some restrictions on the use of forall; what
would it mean if show(x(j),y(j)) were assigned to twice, perhaps by
different values? For correct and consistent results, this case must
be avoided (by the programmer). The compiler permits only simple
arithmetic operations and intrinsics to be used on the left-hand-side
of statements inside forall constructs.
Now we go on to discuss some other operation supported in CMF.
Array Constructors.
A = 0 ! scalar extension to an array
B = [1,2,3,4] ! array constructor
X = [1:n] ! real sequence 1.0, 2.0, ..., n
I = [0:100:4] ! integer sequence 0, 4, 8, ... 100
! note difference from Matlab syntax: (0:4:100)
C = [ 50[1], 50[2,3] ] ! 50 1s followed by 50 pairs of 2,3
call CMF_Random(A) ! fill A with random numbers
Conditional Operation. "Where"s may not be nested. Only assignment is permitted in the body of a "where". "Forall" as well as most intrinsic functions take optional boolean mask arguments.
force = (3,0)*(fishp*ii)/(max(abs(fishp),0.01)) - fishp
could be written
dist = .01
where (abs(fishp) > dis) dist = abs(fishp)
force = (3,0)*(fishp*ii)/dist - fishp
or
dist = .01
far = abs(fishp) > .01
where (far) dist = abs(fishp)
force = (3,0)*(fishp*ii)/dist - fishp
or
where ( abs(fishp) .ge. .01 )
dist = abs(fishp)
elsewhere
dist = .01
endwhere
force = (3,0)*(fishp*ii)/dist - fishp
or
forall ( j = 1:nfish, abs(fishp(j)) > .01 )
force(j) = (3,0)*(fishp(j)*ii)/abs(fishp(j) - fishp(j)
Array Sections. A portion of an array is defined by a triplet in each dimension. It may appear wherever an array is used.
A(3) ! third element
A(1:5) ! first 5 element
A(:5) ! same
A(1:10:2) ! odd elements in order
A(10:-2:2) ! even elements in reverse order
A(1:2,3:5) ! 2-by-3 subblock
A(1,:) ! first row
A(:,j) ! jth column
Implicit Communication. Operations on conformable array sections may require interprocessor communication.
A( 1:10, : ) = B( 1:10, : ) + B( 11:20, : )
DA( 1:n-1 ) = ( A( 1:n-1 ) + A( 2:n ) ) / dt ! finite differences
C( :, 1:5:2 ) = C( :, 2:6:2 ) ! shift noncontiguous sections
D = D( 10:1:-1 ) ! permutation (reverse)
A = [1,0,2,0,0,0,4]
I = [1,3,7]
B = A(I) ! B = [1,2,4] "gather"
C(I) = B ! C = A "scatter", no duplicates in I
D = A([ 1, 1, 3, 3 ]) ! replication
B = CSHIFT( A, 1 ) ! B = [4,1,0,2,0,0,0], circular shift
B = EOSHIFT( A, -1 ) ! B = [0,2,0,0,0,4,0], end-off shift
B = TRANSPOSE( H ) ! matrix transpose
B = SPREAD(A,2,3) ! if B is 3-by-7 then
! B = [ 1,0,2,0,0,0,4 ]
! [ 1,0,2,0,0,0,4 ]
! [ 1,0,2,0,0,0,4 ]
To illustrate some of these operations,
let us compare the Matlab and
CMF solution of the second
Sharks and Fish problem, fish moving
with gravity. (You should pop up the source code for these two
programs in separate windows.) As you can see, they are quite similar.
The main difference between simulating gravity and current is this: With current, the force on each fish is independent of the force on any other fish, and so can be computed very simply in parallel for constant work per fish. With gravity, the force on each fish depends on the locations of all the other fish:
for i = 1 to number_of_fish
force_on_fish(i) = 0
for j = 1 to number_of_fish
if (j .ne. i)
force_on_fish(i) += force on fish i from fish j
endif
endfor
endfor
This straightforward algorithm requires all fish to communicate with all
other fish, and does work growing proportionally to the number_of_fish
per fish. Later, we will examine faster algorithms that only do a
logarithmic amount of work or less per fish, but for now we will stick
with the simple algorithm.
Matlab:
nfish = length(fishp);
perm = [nfish,(1:nfish-1)];
force = 0;
fishpp=fishp;
fishmp=fishm;
for k=1:nfish-1,
fishpp = fishpp(perm);
fishmp = fishmp(perm);
dif = fishpp - fishp;
force = force + fishmp .* fishm .* dif ./ max(abs(dif).^2,1e-6) ;
end
CMF:
force = 0
fishpp = fishp
fishmp = fishm
do k=1, nfish-1
fishpp(1:nfish) = cshift(fishpp(1:nfish), DIM=1, SHIFT=-1)
fishmp(1:nfish) = cshift(fishmp(1:nfish), DIM=1, SHIFT=-1)
dif = fishpp - fishp
force = force + fishmp * fishm * dif / (abs(dif)*abs(dif))
enddo
Both algorithm work as follows. The fish positions fishp and fish
masses fishm are copied into other arrays fishpp and fishmp, respectively.
Then fishpp and fishmp are "rotated" nfish-1 times, so that each
fish in fishp is aligned once with each fish in fishpp. For example, after
step j, fishpp(i) contains the position of fishp(i+j), where i+j wraps
around to 1 modulo nfish. This lets each fish "visit" every other fish to
make the necessary force calculation. The rotation is done in Matlab by
subscripting by the array perm of rotated subscripts. This could be done
in CMF as well, but it is faster to use the built in circular shift
operations cshift.
Scan, or "Parallel Prefix" operations. We discuss these briefly here, and return to them in a later lecture on algorithms.
forall (i=1:5) B(i) = SUM( A( 1:i ) ) ! forward running sum
CMF_SCAN_ADD( B, A, ... ) ! built in scan operation
INTS = [1:n]
forall (i=1:n) FACT( i ) = PRODUCT( INTS( 1:i ) ! factorial
CMF_SCAN_MUL( FACT, INT, ... )
Data Layout. Whether or not a statement will be executed in parallel depends on where it is "laid out" in the machine. An array spread across all p processors can hope to enjoy p-fold parallelism in operations, whereas one stored only on the "host processor" will run sequentially. Briefly, scalar data and arrays which do not participate in any array operations (like A=B+C) reside on the host, and the rest are spread over the machine. There are also compiler directive to help insure that arrays are laid out the way the user wants them to be.
REAL A(64,8), B(64,8), C(64,8)
CMF$ LAYOUT A( :NEWS, :SERIAL ), B( :NEWS, :SERIAL ), C( :SERIAL, :NEWS )
A = B
A = C
In this code fragment, the CMF$ LAYOUT compiler directive is used to
tell CMF where to store the arrays A, B, C. Suppose to we have a 64 processor
machine. There are (at least!) two natural ways to store a 64-by-8 array:
Mem 0 Mem 1 ... Mem 64
A(1,1) A(2,1) ... A(64,1)
A(1,2) A(2,2) ... A(64,2)
... ... ...
A(1,8) A(2,8) ... A(64,8)
and
Mem 0 Mem 1 ... Mem 7 Mem 8 ... Mem 64
C(1,1) C(1,2) ... C(1,8) xxx ... xxx
C(2,1) C(2,2) ... C(2,8) xxx ... xxx
... ... ...
C(64,1) C(64,2) ... C(64,8) xxx ... xxx
The former is specified by A( :NEWS, :SERIAL ), which says the first
subscript should be stored with different values corresponding to
different parallel memories, and different values of the second subscript
should be stored sequentially in the same processor memory. Thus, there
is parallel available in the :NEWS direction, but not in the :SERIAL
direction. :NEWS is a historical term from the CM-2 where it referred
to the parallel connections to the nearest processors in the
North-East-West-South directions.
Since A and B have the same layout, the statement A=B is perfectly parallel. On the other hand, A=C amounts essentially to a matrix transpose, a large amount of communication. When optimizing programs for time, it is essential to make sure layouts are chosen to minimize communication. When in doubt, calling CMF_describe_array(A) will print out a detailed description of the layout of the argument array.
Libraries and Intrinsics. CM Fortran has a very large library of routines available for moving data and doing numerical computations. If you can find an appropriate library routine, it will often run faster than coding it oneself. CMSSL (CM Scientific Subroutine Library) contains many routines for basic linear algebra (BLAS), solving systems of linear equations, finding eigenvalues, doing FFTs, etc., and is highly optimized for the CM-5. We will discuss algorithms used by CMSSL and similar libraries later in the course.
Documentation for the CM-5 may be found in the course reference material, or by logging in to rodin and typing cmview.