A Look at Some Parallel Architectures (continued)

(CS 267, Feb 16 1995)

We continue our discussion of communication networks from Lecture 9.

Rings, Meshes and Toruses. A ring is a one dimensional network, with processors connected to their neighbors on the left and right, with the leftmost and rightmost processors also connected. A 2D mesh is a rectangular array of processor, with each connected to its North, East, West and South neighbors. If the leftmost and rightmost processors in each row are connected, and the top and bottom processor in each column are connected, the network is called a torus. Extensions to higher dimensions are obvious. The diameter of a d-dimensional mesh is d*p^(1/d), and its bisection width is p^((d-1)/d). The torus is somewhat better connected. The Intel Paragon used a 2D torus, and the Cray T3D is a 3D torus (whence its name).

Trees and Fat Trees. A (binary) tree consists of processors either at all the nodes of a tree, connected to parents and children, or it consists of processors at the leaves of a tree, with routing processors at the internal nodes. We will consider the latter case, since it corresponds to the CM-5 data network (the CM-5 has two other networks as well, which we discuss later). The diameter of a tree is 2 log_2 p, which corresponds to sending data from the leftmost leaf via the root to the rightmost leaf. The bisection width is merely 1, since if the p/2 leftmost processors try to send to the p/2 rightmost processors, they all have to pass through the root one at a time. Since the root is a bottleneck, the CM-5 uses what is called a fat-tree, which can be thought of as a tree with fat edges, where the edges at level k have two (or more) times the capacity as the edges as level k+1 (the root is level 0). In reality, this means that a child has two (or more) parents, as shown in the figure below.

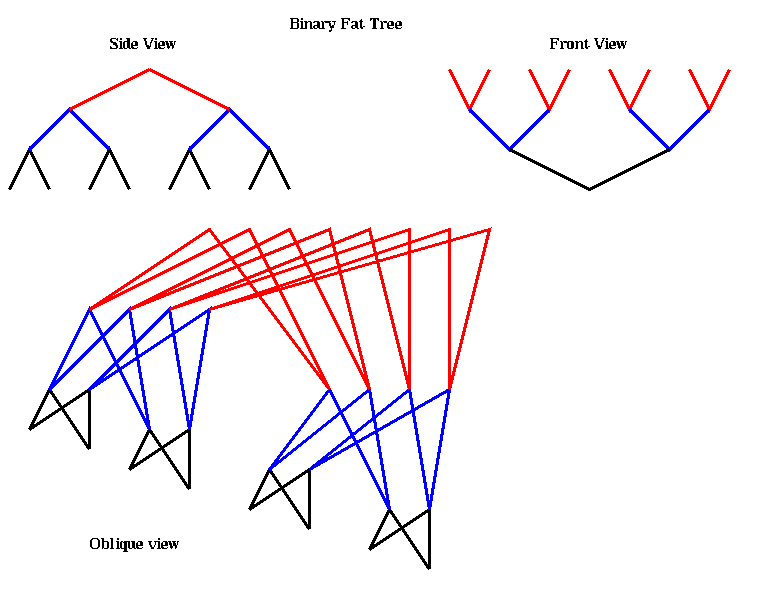
A message is routed from processor i to processor j as follows. All the processors are at the leaves (the bottom), and the other nodes are routing processors. Starting from processor i, a message moves up the tree along the unique path taking it to the first possible common ancestor of i and j in the tree. There are many possible paths (a choice of two at each routing processor), so the routing processor chooses one at random in order to balance the load in the network. Upon reaching this first common ancestor, the message is then routed back down along the unique path connecting it to j. The diameter of this network is 2 log_2 p, and the bisection width is p/2

It is possible to have non-binary fat tree; the CM-5 uses a 4-way tree. It is also unnecessary to double the number of wires at each level; the CM-5 save some wires (and so cost) by having fewer wires at the top of the tree. The resulting maximum bandwidths are:

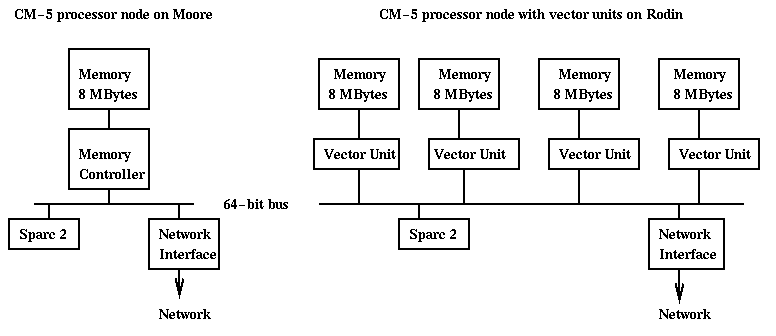
   Among  4 nearest processors:  20 MBytes/sec
   Among 16 nearest processors:  10 MBytes/sec
   Among remaining  processors:   5 MBytes/sec

Some of this bandwidth is used up in message headers, as mentioned below. Here is a little more detail on the CM-5 data network. The vector units perform fast floating point operations, up to 32 Mflops per unit, for a total of 128 Mflops per node. CMF will automatically generate code using the vector units. To use the vector units from Split-C, one can call the CM-5 numerical library CMSSL (click here for details). The local memory hierarchy on a CM-5 node with vector units is rather complicated, and it turns out that data to be operated on by the vector units must be copied from the memory Split-C data resides in to the segment accessible by the vector units. This copying is done at the speed of the much slower Sparc 2 chip. Unless the CMSSL operation is complicated enough, the copy time may overwhelm the time to do the operation. For example, matrix-matrix multiplication takes O(n^3) flops so copying O(n^2) data is probably well worth it. But matrix-vector multiplication takes only O(n^2) flops and so is not worth using the vector units. The difficulty of using the vector units was a major problem in using the CM-5 effectively, and future architectures are unlikely to mimic it. In particular, the fastest microprocessors have floating point integrated on the same chip as the rest of the CPU and (level 1) cache.

To send a message a processor does the following 3 steps:

It stores the first word of the message in the send_first_register. This is actually a register on a special network interface chip, but is memory mapped into the processor address space so the processor can just store to it. This indicates the start of a new message, plus a message tag (from 0 to 5).

The processor stores the remainder of the message (up to 5 words) into the send_register (which is memory mapped again). The first word is the number of the destination processor.

Since the message may fail to be sent if the network is full, the program must check some status bits to see if it has actually been sent (once sent, delivery is guaranteed provided the destination processor continues to receive messages). If the send_OK flag is not sent, the message must be retransmitted.

To receive a message, a processor uses the following three steps

It checks the receive_OK flag, or lets itself be interrupted.

It checks the input message tag, and the length.

It reads consecutive words from the receive_register.

Note that there is no place in the message for a process ID, to distinguish message from different user processes. This means the machine does not support multiprogramming. It is, however, time-shared, which means the entire data network must be flushed and restored on a context switch ("all fall down" mode).

To prevent deadlock, processors must receive as many messages as they send, to keep the network from backing up. When using CMMD, interrupts are used, so if one has posted an asynchronous receive in anticipation of a message arriving, the processor will be interrupted on arrival, the receive performed, and user-specified handler called (if any). With Split-C, the default is to have interrupts turned off, so it is necessary to poll, or "touch" the network interface periodically to let it have some processor cycles in order to handle pending messages. This is done automatically whenever one does communication. For example at every "global := local" the network will be checked for incoming messages. If one does no communication for a long time, the possibility exists that message will back up and the machine will hang. This is unlikely in a program which does communication on a periodic basis, but nonetheless calling splitc_poll() will "check the mailbox", just in case. (Interrupts can be turned off or on in CMMD with CMMD_{disable,enable}_interrupts, and polling done with CMMD_poll().)

Aside on Active Messages

Here is what goes inside a message. The most basic sequence of events that can happen when a message arrives is this: the first word of the data is used as a pointer to some procedure on the receiving processor, which then is executed, using the remaining words in the message as arguments. This is called an active message. The active message can in principle do anything, but typically does one of the following things:

It may "put" one of the data words in a location specified by another data word, and send an acknowledgement back. This is what happens with "global = local" or "global := local".

It may "store" one of the data words in a location specified by another data word, not send an acknowledgement back, but keep a counter of the number of bytes of data received. This is what happens with "global :- local".

It may "get" data located at a memory location in one of the data words, and send it back to the source of the active message. This is what happens with "local = global" or "local := global".

If may receive data returned by an earlier active message request (get or read), store it in memory, and update a counter of the number of bytes received.

It may do any user-specified action. This should be short and run to completion with doing any blocking communication.

More complicated communication protocols, such as blocking send/receive, can be built from active messages as well, but on the CM-5 and many other machines, active messages are the most basic objects that one sends in the network. For more details, click here.

Hypercubes. A d-dimensional hypercube consists of p=2^d processors, each one with a d-bit address. Processor i and j are connected if there addresses differ in exactly one bit. This is usually visualized by thinking of the unit (hyper) cube embedded in d-dimensional Euclidean space, with one corner at 0 and lying in the positive orthant. The processors can be thought of as lying at the corners of the cube, with their (x1,x2,...,xd) coordinates identical to their processor numbers, and connected to their nearest neighbors on the cube.

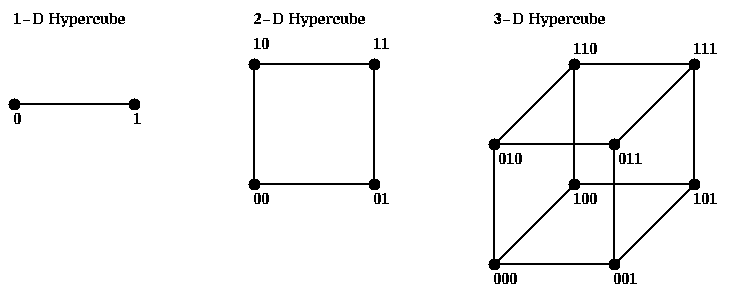
Routing messages may be done by following the edges of the hypercube in paths defined by binary reflected Gray Code. A d-bit Gray Code is a permutation of the integers from 0 to 2^d-1 such that adjacent integers in the list (as well as the first and last) differ by only one bit in their binary expansions. This makes them nearest neighbors in the hypercube. On way to construct such a list is recursively. Let

    G(1) = { 0, 1 }

be the 1-bit Gray code. Given the d-bit Gray code

    G(d) = { g(0), g(1), ... , g(2^d-1) } ,

the d+1-bit code G(d+1) is defined as

    G(d+1) = { 0g(0), 0g(1), ... , 0g(2^d-1), 1g(2^d-1), ... , 1g(1), 1g(0) }

Clearly, if g(i) and g(i+1) differ by one bit, so do the bit patterns in G(d+1). For example,

    G(3) = { 000, 001, 011, 010, 110, 111, 101, 100 }

We will return to Gray codes below when we discuss collective communication.

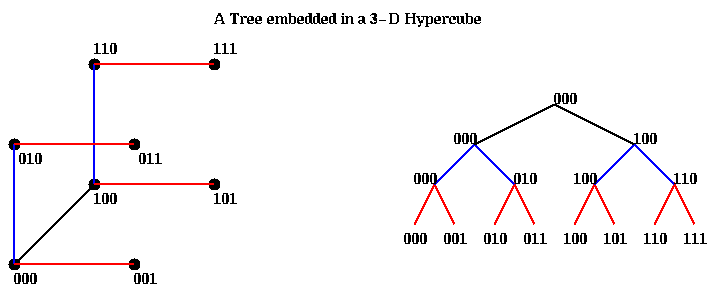
Since there are many more wires in a hypercube than either a tree or mesh, it is possible to embed any of these simpler networks in a hypercube, and do anything these simpler networks do. For example, a tree is easy to embed as follows. Suppose there are 8=p=2^d=2^3 processors, and that processor 000 is the root. The children of the root are gotten by toggling the first address bit, and so are 000 and 100 (so 000 doubles as root and left child). The children of the children are gotten by toggling the next address bit, and so are 000, 010, 100 and 110. Note that each node also plays the role of the left child. Finally, the leaves are gotten by toggling the third bit. Having one child identified with the parent causes no problems as long as algorithms use just one row of the tree at a time. Here is a picture.

Rings are even easier, since the Gray Code describes exactly the order in which the adjacent processors in the ring are embedded.

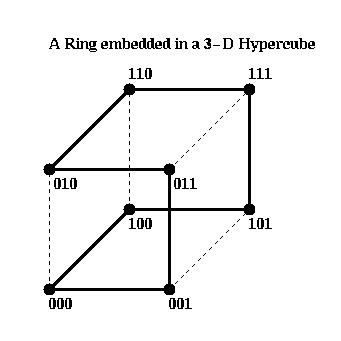
In addition to rings, meshes of any dimension may be embedded in a hypercube, so that nearest neighbors in the mesh are nearest neighbors in a hypercube. The restriction is that mesh dimensions must be powers of 2, and that you need a hypercube of dimension M = m1 + m2 + ... + mk to embed a 2^m1 x 2^m2 x ... x 2^ mk mesh. We illustrate below by embedding a 2x4 mesh in a 3-D hypercube:

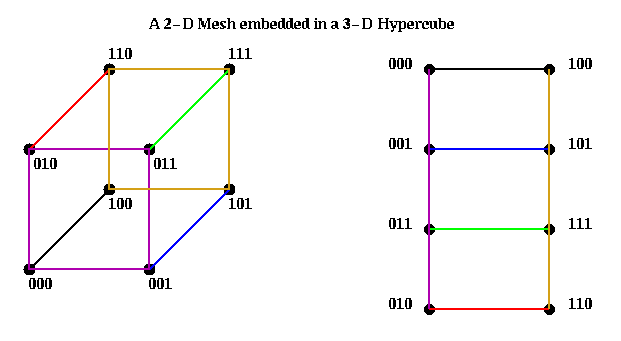
This connection was used in the early series of Intel Hypercubes, and in the CM-2.

Collective communication

Now we discuss a few examples of collective communication, where several processor cooperate to perform a broadcast, reduction, scan, matrix transpose, or other communications where several processors need to cooperate.

Broadcasts and Reductions on Trees

Trees are naturally suited for broadcasts, because the root processor simply sends to its children, the children send to their children, and so on until the broadcast is complete after log_2 p steps. Reduction with an associative operation like addition is similar, with the leaf nodes sending their data to their common parent, who sums the child values, and send the sum to its parent for analogous treatment. After log_2 p steps, the root has the full sum:

Scans, or Parallel Prefix, on Trees

Recall that the add-scan of a sequence x0,...,xp-1 is

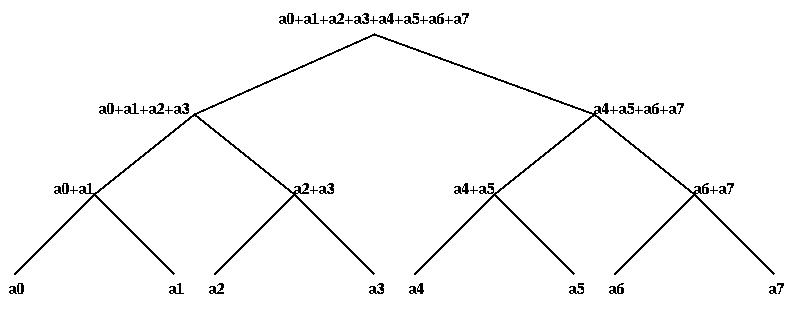
    y0   = x0
    y1   = x0 + x1
    y2   = x0 + x1 + x2
    ...
    yp-1 = x0 + x1 + x2 + ... + xp-1

In what follows, the + operator could be replaced by any other associative operator (product, max, min, matrix multiplication, ...) but for simplicity we discuss addition. We show how to compute y0 through yp-1 in 2*log_2 p -1 steps using a tree.

There are two ways to see the pattern. Perhaps the simplest is the following, where we use the abbreviation i:j, where i <= j, to mean the sum ai+...+aj. The final values at each node are indicated in blue.

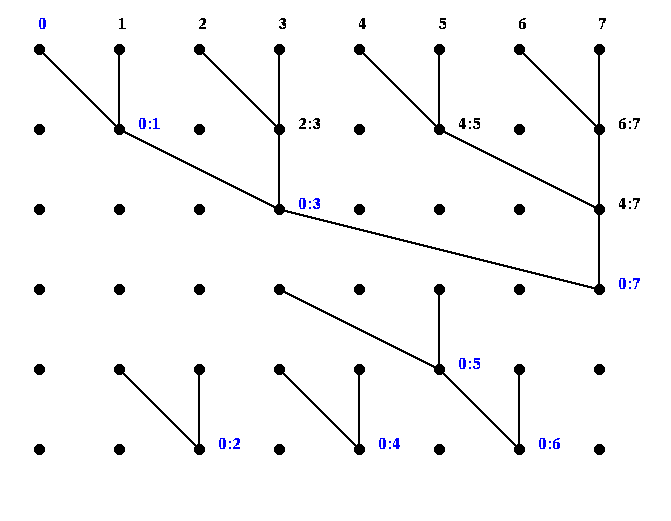
This is actually mapped onto a tree as follows. There is an "up-the-tree" phase, and a "down-the-tree" phase. On the way up, each internal tree node runs the following algorithm.

Get the values L and R from the left and right child, respectively.

Save L in a local register M.

Compute the sum T = L+R, and pass T to the parent.

On the way down, this is the algorithm:

Get a value T from the parent (the root gets 0).

Send T to the left child.

Send T+M to the right child.

On the way up, one can show by induction on the tree that M contains the sum of the leaves of the left subtree at each node. On the way down, one can show by induction that the value T obtained from the parent is the sum of all the leaf nodes to the left of the subtree rooted at the parent. Finally, the value at each leaf is added to the value received from the parent to get the final value. Here is an example.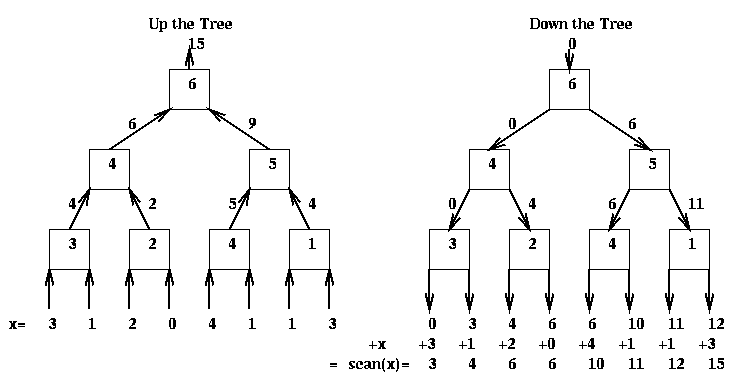

The CM-5 has a second network called the control network, which has a variety of broadcast, reduction and scan operations built into it. Reduction and scan are only supported for logical OR, AND and XOR, as well as signed max, signed integer add, and unsigned integer add. The CM-2 had floating point operations as well, but these were eliminated in the CM-5. It is used by CMMD and Split-C to implement their corresponding high level operations. It performs several other useful operations as well:

Synchronous Global OR. Each processor supplies a bit, blocking until all participate, at which point the logical OR of all the bits is returned to the processors. This is useful for barriers.

Asynchronous Global OR. Each processor supplies a bit, with the global logical OR being constantly computed and updated for each processor. This can be used to test for the first processor to complete a search task, for example.

Broadcasts, reduction and scans could also be done by the data network, and indeed must be done by the data network for more complicated data types (such as floating point) not handled by the control network.

Collective Communication on a Hypercube

As mentioned above, a variety of networks can be embedded in hypercubes, so anything a tree can do, for example, so can a hypercube. A great many more example are described in the text. We describe just one here, which is "Sharks and Fish 2", or "gravity on a hypercube". The simple solution to sharks and fish shown in class uses a single ring along which to pass all the fish. If fact it is possible to embed d = log_2 p "nonoverlapping" ring and use them all at once to get d times the bandwidth. The CM-2 could in fact use all d wires at each node simultaneously. These rings actually do use the same wires, but do so at different times, and so are nonoverlapping in this sense.

If there are n fish, assign n/p to each processor, and further divide these into d groups of m=n/(p*d) fish. Each group F1,...,Fd of m fish will follow a different path through the node on the algorithm. The first path will be defined by the Gray Code G(d) defined above, the second path will consist of left_circular_shift_by_1(G(d)), i.e. each address in the Gray code will have its bits left shifted circularly by 1; this clearly maintains the Gray code property of having adjacent bit patterns differ in just 1 bit. The i-th path will be left_circular_shift_by_i(G(d)). The student is invited to draw a picture of this communication pattern, which uses "all-the-wires-all-the-time", an interesting feature of the CM-2 hypercube network.