
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
Program file for this chapter: pour
You have probably seen puzzles like this one many times:
You are at the side of a river. You have a three-liter pitcher and a seven-liter pitcher. The pitchers do not have markings to allow measuring smaller quantities. You need two liters of water. How can you measure two liters?
These puzzles are used in some IQ tests, so many people come across them in schools. To solve the problem, you must pour water from one pitcher to another. In this particular problem, there are six steps in the shortest solution:
This example is a relatively hard pitcher problem, since it requires six steps in the solution. On the other hand, it doesn't require pouring water back into the river, and it doesn't have any unnecessary pitchers. An actual IQ test has several such problems, starting with really easy ones like this:
You are at the side of a river. You have a three-liter pitcher and a seven-liter pitcher. The pitchers do not have markings to allow measuring smaller quantities. You need four liters of water. How can you measure four liters?
and progressing to harder ones like this:
You are at the side of a river. You have a two-liter pitcher, a five-liter pitcher, and a ten-liter pitcher. The pitchers do not have markings to allow measuring smaller quantities. You need one liter of water. How can you measure one liter?
The goal of this project is a program that can solve these problems. The program should take two inputs, a list of pitcher sizes and a number saying how many liters we want. It will work like this:
? pour [3 7] 4 Pour from river to 7 Pour from 7 to 3 Final quantities are 3 4 ? pour [2 5 10] 1 Pour from river to 5 Pour from 5 to 2 Pour from 2 to river Pour from 5 to 2 Final quantities are 2 1 0
How do people solve these problems? Probably you try a variety of special-purpose techniques. For example, you look at the sums and differences of the pitcher sizes to see if you can match the goal that way. In the problem about measuring four liters with a three-liter pitcher and a seven-liter pitcher, you probably recognized right away that 7−3=4. A more sophisticated approach is to look at the remainders when one pitcher size is divided by another. In the last example, trying to measure one liter with pitchers of two, five, and ten liters, you might notice that the remainder of 5/2 is 1. That means that after removing some number of twos from five, you're left with one.
Such techniques might or might not solve any given pitcher problem. Mathematicians have studied ways to solve such problems in general. To a mathematician, a pitcher problem is equivalent to an algebraic equation in which the variables are required to take on integer (whole number) values. For example, the problem at the beginning of this chapter corresponds to the equation
In this equation, x represents the number of times the three-liter pitcher is filled and y represents the number of times the seven-liter pitcher is filled. A positive value means that the pitcher is filled from the river, while a negative value means that it's filled from another pitcher.
An equation with two variables like this one can have infinitely many solutions, but not all the solutions will have integer values. One integer-valued solution is x=3 and y = -1. This solution represents filling the three-liter pitcher three times from the river (for a total of nine liters) and filling the seven-liter pitcher once from the three-liter pitcher. Since the seven-liter pitcher is bigger than the three-liter pitcher, it has to be filled in stages. Do you see how this analysis corresponds to the sequence of steps I gave earlier?
An equation with integer-valued variables is called a Diophantine equation. In general, a Diophantine equation will have infinitely many solutions, but they won't all be practical as solutions to the original problem. For example, another solution to the equation we've been considering is x = -4 and y=2. This solution tells us to fill the seven-liter pitcher from the river twice, and the three-liter pitcher from the seven-liter pitcher four times. Here's how that works out as a sequence of steps:
This solution works, but it's more complicated than the one I used in the first place.
One way to solve Diophantine equations is graphically. For example, consider the problem about measuring one liter of water with pitcher capacities two, five, and ten liters. It turns out that the ten-liter pitcher is not actually needed, so let's forget it for now and consider the simpler but equivalent problem of using just the two-liter and the five-liter pitchers. This problem gives rise to the equation
For the moment, never mind that we are looking for integer solutions. Just graph the equation as you ordinarily would. The graph will be a straight line; probably the easiest way to draw the graph is to find the x-intercept (when y=0, 2x=1 so x=1/2) and the y-intercept (when x=0, y=1/5).
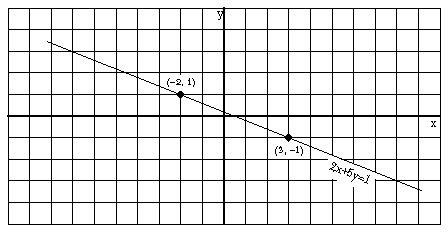
Once you've drawn the graph, you can look for places where the line crosses the grid points of the graph paper. In this case, two such points of intersection are (-2,1) and (3,-1). The first of these points represents the solution shown earlier, in which the five-liter pitcher is filled from the river and then used as a source of water to fill the two-liter pitcher twice. The second integer solution represents the method of filling the two-liter pitcher from the river three times, then pouring the water from the two-liter pitcher to the five-liter pitcher each time. (On the third such pouring, the five-liter pitcher fills up after only one liter is poured, leaving one liter in the two-liter pitcher.) What about the original version of this problem, in which there were three pitchers? In this case, we have a Diophantine equation with three variables:
The graph of this equation is a plane in a three-dimensional coordinate system. An example of a solution point that uses all three pitchers is (-2,-1,1). How would you interpret this as a series of pouring steps?
By the way, not all pitcher problems have solutions. For example, how could you measure one liter with a two-liter pitcher and a ten-liter pitcher? The answer is that you can't; since both pitchers hold an even number of liters, any amount of water measurable with them will also be even.*
*You can find a computational algorithm to solve (or show that there are no solutions to) any linear Diophantine equation with two variables on page 50 of Courant and Robbins, What Is Mathematics? (Oxford University Press, 1941).
My program does not solve pitcher problems by manipulating Diophantine equations. Instead, it simply tries every possible sequence of pouring steps until one of the pitchers contains the desired amount of water. This method is not feasible for a human being, because the number of possible sequences is generally quite large. Computers are better than people at doing large numbers of calculations quickly; people have the almost magical ability to notice the one relevant pattern in a problem without trying all the possibilities. (Some researchers attribute this human ability to "parallel processing"--the fact that the human brain can carry on several independent trains of thought all at once. They are beginning to build computers designed for parallel processing, and hope that these machines will be able to perform more like people than traditional computers.)
The possible pouring steps for a pitcher problem form a tree. The
root of the tree is the situation in which all the pitchers are empty.
Connected to the root are as many branches as there are pitchers; each
branch leads to a node in which one of the pitchers has been filled from the
river. Each of those nodes has several branches connected to it,
corresponding to the several possible pouring steps. Here is the beginning
of the tree for the case of a three-liter pitcher and a seven-liter pitcher.
Each node is represented in the diagram by a list of numbers indicating the
current contents of the three-liter pitcher and the seven-liter pitcher; for
example, the list [3 4] means that the three-liter pitcher is
full and the seven-liter pitcher contains four liters.
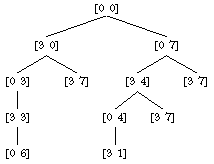
Actually, I have simplified this tree by showing only the meaningful pouring steps. The program must consider, and of course reject, things like the sequence
and individual meaningless steps like pouring from a pitcher into itself, pouring from an empty pitcher, and pouring into a full pitcher. For a two-pitcher problem there are three possible sources of water (the two pitchers and the river) and three possible destinations, for a total of nine possible pouring steps. Here is the top of the full tree:

At each level of the tree, the number of nodes is multiplied by nine. If we're trying to measure two liters of water, a six-step problem, the level of the tree at which the solution is found will have 531,441 nodes! You can see that efficiency will be an important consideration in this program.
In some projects, a tree is represented within the program by a Logo list. That's not going to be the case in this project. The tree is not explicitly represented in the program at all, although the program will maintain a list of the particular nodes of the tree that are under consideration at a given moment. The entire tree can't be represented as a list because it's infinitely deep! In this project, the tree diagram is just something that should be in your mind as a model of what the program is doing: it's searching through the tree, looking for a node that includes the goal quantity as one of its numbers.
Many programming problems can be represented as searches through trees. For example, a chess-playing program has to search through a tree of moves. The root of the tree is the initial board position; the second level of the tree contains the possible first moves by white; the third level contains the possible responses by black to each possible move by white; and so on.
There are two general techniques for searching a tree. These techniques are called depth-first search and breadth-first search. In the first technique, the program explores all of the "descendents" of a given node before looking at the "siblings" of that node. In the chess example, a depth-first search would mean that the program would explore all the possible outcomes (continuing to the end of the game) of a particular opening move, then go on to do the same for another opening move. In breadth-first search, the program examines all the nodes at a given level of the tree, then goes on to generate and examine the nodes at the next level. Which technique is more appropriate will depend on the nature of the problem.
In a
programming language like Logo, with recursive procedures and local
variables, it turns out that depth-first search leads to a simpler program
structure. Suppose that we are given an operation called
children that takes a node as input and gives us as its output
a list of all the children (one level down) of that node. Suppose we also
are given a command called process that takes a node as input
and does whatever the program needs to do for each node of the tree. (You
can just use print in place of process if you want
to see what's in the tree.) Here is how to do a depth-first search:
to depth.first :node process :node foreach (children :node) "depth.first end
In this program, the structure of the tree is reflected in the
structure of recursive invocations of depth.first.
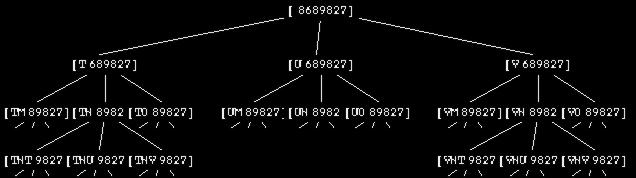
It might be worthwhile to consider a specific example of how this program works. One of the suggested activities in Chapter 11 was to write a program that takes a telephone number as input and prints out all possible spellings of that number as letters. (Each digit can represent any of three letters. To keep things simple, I'm going to ignore the problem of the digits zero and one, which don't represent any letters on telephone dials in the United States.) Here is a partial picture of the tree for a particular telephone number. Each node contains some letters and some digits. (In the program, a node will be represented as a Logo list with two members, a word of letters and a word of digits.) The root node is all digits; the "leaf" nodes will be all letters.
The operation children must output a list of three nodes, selecting
each of the three possible letters for the first remaining digit. If the
input to children is a leaf node (one with all letters), it must
output the empty list to indicate that there are no children for that node.
to children :node
if emptyp last :node [output []]
output map [child (first :node) ? (butfirst last :node)] ~
letters first last :node
end
to letters :digit
output item :digit [[] abc def ghi jkl mno prs tuv wxy]
end
to child :letters :this :digits
output list (word :letters :this) :digits
end
?show children [tnt 9827]
[[tntw 827] [tntx 827] [tnty 827]]
The top-level procedure has to turn a number into a root node and invoke a depth-first search:
to spell :number depth.first list " :number end
What about the process command? The program wants to print only leaf
nodes:
to process :node if emptyp last :node [print :node] end
» Try this program. To get the tree illustrated above, use the instruction
spell 8689827
Then try again, but investigate the order in which the program
searches the nodes of the tree by using a different version of process:
to process :node print :node end
This will let you see the order in which the program encounters the nodes of the tree.
Writing a breadth-first search is a little more complicated because the program must explicitly arrange to process all the nodes of a given level before processing those at the next level. It keeps track of the nodes waiting to be processed in a queue, a list in which new nodes are added at the right and the next node to be processed is taken from the left. Here is the program:
to breadth.first :root
breadth.descend (list :root)
end
to breadth.descend :queue
if emptyp :queue [stop]
process first :queue
breadth.descend sentence (butfirst :queue) ~
(children first :queue)
end
This breadth-first search program uses the same children and
process subprocedures as the depth-first version. You can try a
breadth-first listing of telephone number spellings simply by changing the
top-level spell procedure to invoke breadth.first
instead of depth.first. What you'll find is that (with the
version of process that only prints leaf nodes) the two
versions produce the same results, but the depth-first program trickles the
spellings out one by one, while the breadth-first version prints nothing for
a long time and then spits out all the spellings at once. If you use the
version of process that prints all the nodes, you can see why.
The telephone number speller is an unusual example of a tree-search program for two reasons. First, the tree is finite; we know in advance that it extends seven levels below the root node, because a telephone number has seven digits. Second, the goal of the program requires searching the entire tree. It's more common that the program is looking for a solution that's "good enough" in some sense, and when a solution is found, the program stops looking. For example, in the pitcher problem program, once we find a sequence of steps to measure the desired amount of water, we don't care if there is also a second way to do it.
For the pitcher problem solver, I decided that a breadth-first search is appropriate. The main reason is that I wanted to present the shortest possible solution. To do that, first I see if any one-step sequences solve the problem, then I see if any two-step sequences solve it, and so on. This is a breadth-first order.
At first, I thought that I would represent each node of the tree as a list of numbers representing the contents of the pitchers, as in the diagram I showed earlier. I called this list of quantities a state. This information is enough to be able to generate the children of a node. Later, though, I realized that when I find a winning solution (one that has the goal quantity as one of the quantities in the state list) I want to be able to print not only the final quantities but also the sequence of pouring steps used to get there. In a depth-first search, this information is implicitly contained in the local variables of the procedure invocations leading to the winning solution. In a breadth-first search, however, the program doesn't keep track of the sequence of events leading to a given node. I had to remember this information explicitly.
The solution I chose was to have an extra member in the list representing a state, namely a list of pourings. A pouring is a list of two numbers representing the source and the destination of the water being poured. Zero represents the river; numbers greater than zero are pitcher numbers. (A pitcher number is not the same as the size of the pitcher. If you enter the instruction
pour [2 5 10] 1
then the two-liter pitcher is pitcher number 1, the five-liter is
number 2, and the ten-liter is number 3.) The list of pourings is the first
member of the expanded state list; pourings are added to that list at the
front, with fput. For example, in the interaction
?pour [3 7] 4 Pour from river to 7 Pour from 7 to 3 Final quantities are 3 4
the extended state information for the final solution state is
[[[2 1] [0 2]] 3 4]
In this list, the sublist [0 2] represents pouring water
from the river into pitcher number 2, which is the seven-liter pitcher.
The sublist [2 1] represents pouring water from pitcher number 2 into
pitcher number 1.
Up to this point I've continued to call this expanded data
structure a state. That's what I did in the program, also, until I
found that certain procedures needed the new version, while other procedures
dealt with what I had originally considered a state, with only the final
quantities included in the list. As a result, my program had local
variables named state in several procedures, some of which contained
the old kind of state, and some the new kind. I thought this might be
confusing, so I did what I should have done in the first place: I invented a
new name for the expanded data structure. It's now called a path;
when you read the program you can confidently assume that :state
represents a list like
[3 4]
while :path represents a list like
[[[2 1] [0 2]] 3 4]
The trouble with using a list of lists of lists in a program is that it can
become very complicated to keep track of all the uses of selectors like
first and constructors like fput. For example,
suppose the value of the variable oldpath is a path, and we
decide to pour water from pitcher number :from to pitcher
number :to. We now want to construct a new path, which will
include a new state (computed from the old state and the two pitcher
numbers) and a new list of moves, with the new move added to the existing
ones. We'd end up saying
make "newpath fput (fput (list :from :to) first :oldpath) ~
(newstate butfirst :oldpath :from :to)
assuming that we have a procedure newstate that computes the
new state. This instruction is hard to read! The two invocations of
fput have quite different purposes. One adds a new move to a
list of moves, while the other connects a list of moves to a state in order
to form a path. We can clarify instructions like this one if we make up
synonyms for procedures like first and fput to be
used in particular contexts. For example, we make a new path using
fput, but we'll call it make.path when we're using
it for that purpose. Just as fput is a constructor, and
first a selector, for lists, we can invent constructors and
selectors for abstract data types (ones that we make up, rather
than ones built into Logo) such as paths:
to make.path :moves :state output fput :moves :state end to path.moves :path output first :path end to path.state :path output butfirst :path end
That unreadable instruction shown earlier would now be written this way:
make "newpath make.path (fput (list :from :to) path.moves :oldpath) ~
(newstate (path.state :oldpath) :from :to)
At first glance this may not seem like much of an improvement, since the new
names are longer and less familiar than the old ones. But we can now read
the instruction and see that it calls a constructor make.path
with two inputs, one that seems to have to do with moves, and the other that
seems to have to do with states. If we remember that a path has two parts,
a list of moves and a state, this makes sense.
» Invent a constructor and selectors for a move data type.
Sentence as a CombinerThe general breadth-first search program I showed earlier contains this procedure:
to breadth.descend :queue if emptyp :queue [stop] process first :queue breadth.descend sentence (butfirst :queue) (children first :queue) end
The most common use of sentence is in generating English
sentences. In that use, the input and output lists are sentences or
flat lists. You're supposed to think, "Sentence takes two words or
sentences as inputs; its output is a sentence containing all the words of
the inputs." In this program, we're using sentence in a different
way, more like what is called append in Lisp. Here you're supposed to
think, "Sentence takes two lists as inputs; its output is a list
containing the members of the inputs." Those members could be words or
lists, but in this case they'll be lists, namely paths.
Recursive procedures that manipulate non-flat lists generally use
fput as the combiner. That wouldn't work here for two
reasons. First, the queue structure that we need to implement breadth-first
search requires that we add new entries at the opposite end of the list from
where we look for the next node to process. If we use first to
select a node and fput to add new candidate nodes, then instead
of a queue we'd be using a stack, in which the newest entries are
processed first instead of the oldest ones first. That would give us a
depth-first tree search algorithm. We could solve that problem by using
lput as the combiner, but the second reason for choosing
sentence is that we don't generate new entries one at a time.
Instead, children gives us several children to add to the queue
at once. That means we must append the list output by children
to the list that represents the nodes already queued.
Pour is going to work essentially by invoking breadth.first on a
root node containing zeros for all the current quantities. But in this case
we want to pick a single node that satisfies the conditions of the problem,
so we must modify breadth.first to make it an operation that
outputs the first such node:
to breadth.first :root
output breadth.descend (list :root)
end
to breadth.descend :queue
if emptyp :queue [output []]
if winnerp first :queue [output first :queue]
output breadth.descend sentence (butfirst :queue) ~
(children first :queue)
end
The predicate winnerp will output true if its input is
a node that satisfies the problem conditions:
to winnerp :path output memberp :goal path.state :path end
If breadth.first runs out of nodes without finding a
solution, it returns an empty list to indicate failure.
Here is a
simplified version of pour:
to pour :sizes :goal win breadth.first make.path [] all.empty :sizes end to all.empty :list output map [0] :list end
All.empty is an operation that outputs a state in which all
of the values are zeros. The number of zeros in the list is equal to the
number of members in its input, which is the number of pitchers. Pour
combines this initial state with an empty list of moves to produce the
first path.
To allow breadth.first to work, we must have an operation
called children that outputs a list of the children of a node.
Starting from a particular state, what are the possible outcomes of a single
pouring? As I mentioned earlier, the source of a pouring can be the river
or any of the pitchers, and the destination can also be the river or any of
the pitchers. If there are n pitchers, then there are n+1
sources, n+1 destinations, and therefore (n+1)2
possible pourings. Here is how the program structure reflects this. I'm
assuming that we've created (elsewhere in the program) a variable called
pitchers whose value is a list of all the integers from zero to
n.
to children :path
output map.se [children1 :path ?] :pitchers
end
to children1 :path :from
output map.se [child :path :from ?] :pitchers
end
to child :path :from :to
output (list make.path (fput (list :from :to) path.moves :path)
(newstate (path.state :path) :from :to))
end
The version of child presented here is simpler than the one
in the actual project, but the other procedures are the real versions.
We'll see later how child is expanded. The immediately important
point is to see how children and children1 ensure that every
possible source (:from) and destination (:to) from zero to the
number of pitchers are used.
You should be wondering, at this point, why children1 uses
sentence as a combiner. (That's what it means to use
map.se rather than map.) It makes sense for
children to combine using sentence because, as I
discussed earlier, the things it's combining are lists of nodes, the outputs
from invocations of children1. But children1 is
not combining lists of nodes; it's combining the outputs from invocations of
child. Each invocation of child computes a single
child node. It would be more straightforward to write the program this way:
to children1 :path :from ;; simplified
output map [child :path :from ?] :pitchers
end
to child :path :from :to ;; simplified
output make.path (fput (list :from :to) path.moves :path) ~
(newstate (path.state :path) :from :to)
end
This also eliminates the use of list in child, needed
in the other version to turn a single node into a singleton (one-member)
list of nodes, which is what sentence needs to function properly as a
combiner.
The reason for the use of sentence in children1 is that we are
later going to modify child so that sometimes it rejects a possible
new node for efficiency reasons. For example, it makes no sense to have
nodes for pourings in which the source and the destination are the same.
When it wants to reject a node, child will output the empty list.
Using sentence as the combiner, this empty list simply doesn't affect
the accumulated list of new nodes. Here is a version of child
modified to exclude pourings to and from the same place:
to child :path :from :to
if equalp :from :to [output []]
output (list make.path (fput (list :from :to) path.moves :path)
(newstate (path.state :path) :from :to))
end
With this version of child, the use of sentence in
children1 may seem more sensible to you.
To create the variable pitchers we modify the top-level pour:
to pour :sizes :goal local "pitchers make "pitchers fput 0 (map [#] :sizes) win breadth.first make.path [] all.empty :sizes end
Here we are taking advantage of a feature of map that I haven't
mentioned earlier. The number sign (#) can be used in a
map template to represent the position in the input, rather
than the value, of a member of the input data list. That is,
# is replaced by 1 for the first member, 2 for the second, and
so on. In this example, these position numbers are all we care about; the
template does not contain the usual question mark to refer to the values of
the data.
The job of child is to produce a new child node, that is to say, a new
path. Its inputs are an old path and the source and destination of a new
pouring. The new path consists of a new state and a new list of pourings.
The latter is easy; it's just the old list of pourings with the new one
inserted. Child computes that part itself, with the expression
fput (list :from :to) path.moves :path
The new state is harder to compute. There are four cases.
Here is the procedure to carry out these computations:
to newstate :state :from :to
if riverp :to [output replace :state :from 0]
if riverp :from [output replace :state :to (size :to)]
if (water :from) < (room :to) ~
[output replace2 :state ~
:from 0 ~
:to ((water :from)+(water :to))]
output replace2 :state ~
:from ((water :from)-(room :to)) ~
:to (size :to)
end
Each instruction of this procedure straightforwardly embodies one of the four numbered possibilities.
Helper procedures are used to compute a new list of amounts of water, replacing either one or two old values from the previous list:
to replace :list :index :value
if equalp :index 1 [output fput :value butfirst :list]
output fput first :list (replace butfirst :list :index-1 :value)
end
to replace2 :list :index1 :value1 :index2 :value2
if equalp :index1 1 ~
[output fput :value1 replace butfirst :list :index2-1 :value2]
if equalp :index2 1 ~
[output fput :value2 replace butfirst :list :index1-1 :value1]
output fput first :list ~
replace2 butfirst :list :index1-1 :value1 :index2-1 :value2
end
Replace takes as inputs a list, a number
representing a position in the list, and a value. The output is a copy of
the first input, but with the member selected by the second input replaced
with the third input. Here's an example:
?show replace [a b c d e] 4 "x [a b c x e]
Replace2 has a similar purpose, but its output has
two members changed from their values in the input list.
Remember that newstate has as one of its inputs a state, that
is, a list of numbers representing quantities of water.
Newstate uses replace to change the amount of
water in one of the pitchers. The second input to replace is
the pitcher number, and the third is the new contents of that pitcher. For
example, if the destination is the river then we want to empty the source
pitcher. This case is handled by the instruction
if riverp :to [output replace :state :from 0]
If the destination is the river,
the output state is the same as the input state except that the pitcher
whose number is :from has its contents replaced by zero. The other
cases are handled similarly, except that two replacements are necessary if
both source and destination are pitchers.
The instructions in newstate use some procedures I haven't written
yet, such as riverp to test whether a source or destination is the
river, and room to find the amount of empty space in a pitcher.
If we think of a pitcher as an abstract data type, then these can be
considered selectors for that type. Here they are:
to riverp :pitcher output equalp :pitcher 0 end to size :pitcher output item :pitcher :sizes end to water :pitcher output item :pitcher :state end to room :pitcher output (size :pitcher)-(water :pitcher) end
To underscore the importance of data abstraction, here is what newstate
would look like without these selectors. (I actually wrote it this way at
first, but I think you'll agree that it's unreadable.)
to newstate :state :from :to
if equalp :to 0 [output replace :state :from 0]
if equalp :from 0 [output replace :state :to (item :to :sizes)]
if ((item :from :state) < ((item :to :sizes)-(item :to :state))) ~
[output replace2 :state ~
:from 0 ~
:to ((item :from :state)+(item :to :state))]
output replace2 :state ~
:from ((item :from :state)-
((item :to :sizes)-(item :to :state))) ~
:to (item :to :sizes)
end
When breadth.first finds a winning path, the top-level procedure
pour invokes win with that path as its input.
Win's job is to print the results. Since the list of moves is
kept in reverse order, win uses the Logo primitive operation
reverse to ensure that the moves are shown in chronological
order.
to win :path
if emptyp :path [print [Can't do it!] stop]
foreach (reverse path.moves :path) "win1
print sentence [Final quantities are] (path.state :path)
end
to win1 :move
print (sentence [Pour from] (printform first :move)
[to] (printform last :move))
end
to printform :pitcher
if riverp :pitcher [output "river]
output size :pitcher
end
The pour program as described so far would run extremely slowly. The
rest of the commentary in this chapter will be on ways to improve its
efficiency. The fundamental problem is one I mentioned earlier: the
number of nodes in the tree grows enormously as the depth increases. In a
problem with two pitchers, the root level has one node, the next level nine
nodes, the third level 81, the fourth level 729, the fifth level 6561, and
the sixth level 59049. A six-step problem like
pour [3 7] 2
would strain the memory capacity of many computers as well as taking forever to run!
When you're trying to make a program more efficient, the easiest
improvements to figure out are not usually the ones that really help. The
easy things to see are details about the computation within some procedure.
For example, the newstate procedure described earlier calls the
room procedure twice to compute the amount of room available in
the destination pitcher. Each call to room computes the
quantity
(item :to :sizes)-(item :to :state)
This expression represents the amount of empty space in the destination pitcher. Perhaps it would be faster to compute this number only once, and store it in a variable? I haven't bothered trying to decide, because the effect is likely to be small either way. Improving the speed of computing each new node is much less important than cutting down the number of nodes we compute. The reason is that eliminating one node also eliminates all its descendants, so that the effect grows as the program moves to lower levels of the tree.
The best efficiency improvement is likely to be a complete rethinking of the algorithm. For example, I've mentioned that a numerical algorithm exists for solving two-variable linear Diophantine equations. This algorithm would be a much faster way to solve two-pitcher problems than even the best tree search program. I haven't used that method because I wanted a simple program that would work for any number of pitchers, but if I really had to solve such problems in practice, I'd use the Diophantine equation method wherever possible.
We have already modified child to avoid one kind of meaningless
pouring, namely ones in which the source is the same as the destination.
Two other avoidable kinds of meaningless pourings are ones from an empty
source and ones to a full destination. In either case, the quantity of
water poured will be zero, so the state will not change. Here is a modified
version of child that avoids these cases:
to child :path :from :to
local "state
if equalp :from :to [output []]
make "state path.state :path
if not riverp :from ~
[if equalp (water :from) 0 [output []]]
if not riverp :to ~
[if equalp (water :to) (size :to) [output []]]
output (list make.path (fput list :from :to path.moves :path)
(newstate :state :from :to))
end
The local variable state is set up because the procedure
water needs it. (Water relies on Logo's dynamic scope to give
it access to the state variable provided by its caller.)
The important changes are the two new if instructions. The first
avoids pouring from an empty pitcher; the second avoids pouring into a full
one. In both cases, the test makes sense only for actual pitchers; the
river does not have a size or a current contents.
To underscore what I said earlier about what's important in trying to improve the efficiency of a program, notice that these added tests slow down the process of computing each new node, and yet the overall effect is beneficial because the number of nodes is dramatically reduced.
It's relatively easy to find individual pourings that are absurd. A harder problem is to avoid sequences of pourings, each reasonable in itself, that add up to a state we've already seen. The most blatant examples are like the one I mentioned a while back about filling a pitcher from the river and then immediately emptying it into the river again. But there are less blatant cases that are also worth finding. For example, suppose the problem includes a three-liter pitcher and a six-liter pitcher. The sequence
Pour from river to 6 Pour from 6 to 3
leads to the same state ([3 3]) as the sequence
Pour from river to 3 Pour from 3 to 6 Pour from river to 3
The latter isn't an absurd sequence of pourings, but it's silly to pursue any of its children because they will have the same states as the children of the first sequence, which is one step shorter. Any solution that could be found among the descendents of the second sequence will be found one cycle earlier among the descendents of the first.
To avoid pursuing these duplicate states, the program keeps a list of all
the states found so far. This strategy requires changes to pour and
to child.
to pour :sizes :goal local [oldstates pitchers] make "oldstates (list all.empty :sizes) make "pitchers fput 0 (map [#] :sizes) win breadth.first make.path [] all.empty :sizes end to child :path :from :to local [state newstate] if equalp :from :to [output []] make "state path.state :path if not riverp :from ~ [if equalp (water :from) 0 [output []]] if not riverp :to ~ [if equalp (water :to) (size :to) [output []]] make "newstate (newstate :state :from :to) if memberp :newstate :oldstates [output []] make "oldstates fput :newstate :oldstates output (list make.path (fput list :from :to path.moves :path) :newstate) end
The change in pour is simply to initialize the list of
already-seen states to include the state in which all pitchers are empty.
There are two important new instructions in child. The first
rejects a new node if its state is already in the list; the second adds a
new state to the list. Notice that it is duplicate states we look
for, not duplicate paths; it's in the nature of a tree-search
program that there can never be duplicate paths.
The breadth-first search mechanism we're using detects a winning path as it's removed from the front of the queue. If we could detect the winner as we're about to add it to the queue, we could avoid the need to compute all of the queue entries that come after it: children of nodes that are at the same level as the winning node, but to its left.
It's not easy to do this elegantly, though, because we add new nodes to the
queue several at a time, using the procedure children to compute them.
What we need is a way to let child, which constructs the winning node,
prevent the computation of any more children, and notify breadth.first
that a winner has been found.
The most elegant way to do this in Berkeley Logo uses a primitive called
throw that we won't meet until the second volume of this series.
Instead, in this chapter I'll use a less elegant technique, but one that
works in any Logo implementation. I'll create a variable named won
whose value is initially false but becomes true as soon as a
winner is found. Here are the necessary modifications:
to pour :sizes :goal
local [oldstates pitchers won]
make "oldstates (list all.empty :sizes)
make "pitchers fput 0 (map [#] :sizes)
make "won "false
win breadth.first make.path [] all.empty :sizes
end
to breadth.descend :queue
if emptyp :queue [output []]
if :won [output last :queue]
op breadth.descend sentence (butfirst :queue) ~
(children first :queue)
end
to child :path :from :to
local [state newstate]
if :won [output []]
if equalp :from :to [output []]
make "state path.state :path
if not riverp :from ~
[if equalp (water :from) 0 [output []]]
if not riverp :to ~
[if equalp (water :to) (size :to) [output []]]
make "newstate (newstate :state :from :to)
if memberp :newstate :oldstates [output []]
make "oldstates fput :newstate :oldstates
if memberp :goal :newstate [make "won "true]
output (list make.path (fput list :from :to path.moves :path) :newstate)
end
The procedure winnerp is no longer used; we are now checking
a state, rather than a path, for the goal amount.
» Is it possible to eliminate more pieces of the tree by more sophisticated analysis of the problem? For example, in all of the specific problems I've presented, the best solution never includes pouring from pitcher A to pitcher B and then later pouring from B to A. Is this true in general? If so, many possible pourings could be rejected with an instruction like
if memberp list :to :from path.moves :path [output []]
in child.
» Do some research into Diophantine equations and the techniques used to solve them computationally. See if you can devise a general method for solving pitcher problems with any number of pitchers, based on Diophantine equations.
» Think about writing a program that would mimic the way people actually approach these problems. The program would, for example, compute the differences and remainders of pairs of pitcher sizes, looking for the goal quantity.
» What other types of puzzles can be considered as tree searching problems?
| (back to Table of Contents) | BACK chapter thread NEXT |
;; Initialization
to pour :sizes :goal
local [oldstates pitchers won]
make "oldstates (list all.empty :sizes)
make "pitchers fput 0 (map [#] :sizes)
make "won "false
win breadth.first make.path [] all.empty :sizes
end
to all.empty :list
output map [0] :list
end
;; Tree search
to breadth.first :root
op breadth.descend (list :root)
end
to breadth.descend :queue
if emptyp :queue [output []]
if :won [output last :queue]
op breadth.descend sentence (butfirst :queue) ~
(children first :queue)
end
;; Generate children
to children :path
output map.se [children1 :path ?] :pitchers
end
to children1 :path :from
output map.se [child :path :from ?] :pitchers
end
to child :path :from :to
local [state newstate]
if :won [output []]
if equalp :from :to [output []]
make "state path.state :path
if not riverp :from ~
[if equalp (water :from) 0 [output []]]
if not riverp :to ~
[if equalp (water :to) (size :to) [output []]]
make "newstate (newstate :state :from :to)
if memberp :newstate :oldstates [output []]
make "oldstates fput :newstate :oldstates
if memberp :goal :newstate [make "won "true]
output (list make.path (fput list :from :to path.moves :path) :newstate)
end
to newstate :state :from :to
if riverp :to [output replace :state :from 0]
if riverp :from [output replace :state :to (size :to)]
if (water :from) < (room :to) ~
[output replace2 :state ~
:from 0 ~
:to ((water :from)+(water :to))]
output replace2 :state ~
:from ((water :from)-(room :to)) ~
:to (size :to)
end
;; Printing the result
to win :path
if emptyp :path [print [Can't do it!] stop]
foreach (reverse path.moves :path) "win1
print sentence [Final quantities are] (path.state :path)
end
to win1 :move
print (sentence [Pour from] (printform first :move)
[to] (printform last :move))
end
to printform :pitcher
if riverp :pitcher [output "river]
output size :pitcher
end
;; Path data abstraction
to make.path :moves :state
output fput :moves :state
end
to path.moves :path
output first :path
end
to path.state :path
output butfirst :path
end
;; Pitcher data abstraction
to riverp :pitcher
output equalp :pitcher 0
end
to size :pitcher
output item :pitcher :sizes
end
to water :pitcher
output item :pitcher :state
end
to room :pitcher
output (size :pitcher)-(water :pitcher)
end
;; List processing utilities
to replace :list :index :value
if equalp :index 1 [output fput :value butfirst :list]
output fput first :list (replace butfirst :list :index-1 :value)
end
to replace2 :list :index1 :value1 :index2 :value2
if equalp :index1 1 ~
[output fput :value1 replace butfirst :list :index2-1 :value2]
if equalp :index2 1 ~
[output fput :value2 replace butfirst :list :index1-1 :value1]
output fput first :list ~
replace2 butfirst :list :index1-1 :value1 :index2-1 :value2
end
Brian Harvey,
bh@cs.berkeley.edu