


|
|
Until now we've been using procedures that Scheme already knows when you begin working with it. In this chapter you'll find out how to create new procedures.
A Scheme program consists of one or more procedures. A procedure is a description of the process by which a computer can work out some result that we want. Here's how to define a procedure that returns the square of its argument:
(define (square x) (* x x))
(The value returned by define may differ depending on the
version of Scheme you're using. Many versions return the name of the
procedure you're defining, but others return something else. It doesn't
matter, because when you use define you aren't interested in the
returned value, but rather in the fact that Scheme remembers the new
definition for later use.)
This is the definition of a procedure called square. Square
takes one argument, a number, and it returns the square of that number.
Once you have defined square, you can use it just the same way as you
use primitive procedures:
> (square 7) 49 > (+ 10 (square 2)) 14 > (square (square 3)) 81
This procedure definition has four parts. The first is the word define, which indicates that you are defining something. The second and
third come together inside parentheses: the name that you want to give the
procedure and the name(s) you want to use for its argument(s). This
arrangement was chosen by the designers of Scheme because it looks like the
form in which the procedure will be invoked. That is, (square x) looks
like (square 7). The fourth part of the definition is the body: an expression whose value provides the function's return value.

Define is a special form, an exception to the
evaluation rule we've been going on about.[1] Usually, an expression represents a procedure invocation, so
the general rule is that Scheme first evaluates all the subexpressions, and
then applies the resulting procedure to the resulting argument values. The
specialness of special forms is that Scheme doesn't evaluate all the
subexpressions. Instead, each special form has its own particular
evaluation rule. For example, when we defined square, no
part of the definition was evaluated: not square, not x, and
not (* x x). It wouldn't make sense to evaluate (square x)
because you can't invoke the square procedure before you define it!
It would be possible to describe special forms using the following model:
"Certain procedures want their arguments unevaluated, and Scheme recognizes
them. After refraining from evaluating define's arguments, for
example, Scheme invokes the define procedure with those unevaluated
arguments." But in fact the designers of Scheme chose to think about it
differently. The entire special form that starts with define is just a
completely different kind of thing from a procedure call. In Scheme there
is no procedure named define. In fact, define is not the name
of anything at all:
> + #<PRIMITIVE PROCEDURE +> > define ERROR - INVALID CONTEXT FOR KEYWORD DEFINE
Nevertheless, in this book, unless it's really important to make
the distinction, we'll talk as if there were a procedure called define.
For example, we'll talk about "define's arguments" and "the value
returned by define" and "invoking define."
Throughout most of this book, our procedures will describe processes that
compute functions. A function is a connection between some values
you already know and a new value you want to find out. For example, the
square function takes a number, such as 8, as its input value and
returns another number, 64 in this case, as its output value. The plural function takes a noun, such as "computer," and returns another
word, "computers" in this example. The technical term for the function's
input value is its argument. A function may take more than one
argument; for example, the remainder function takes two arguments,
such as 12 and 5. It returns one value, the remainder on dividing the first
argument by the second (in this case, 2).
We said earlier that a procedure is "a description of the process by which a computer can work out some result that we want." What do we mean by process? Consider these two definitions:
(define (f x) (+ (* 3 x) 12)) (define (g x) (* 3 (+ x 4)))
and we'd say that f and g are two procedures that
represent the same function.
In real life, functions are not always represented by procedures. We could represent a function by a table showing all its possible values, like this:
| Alabama | Montgomery |
| Alaska | Juneau |
| Arizona | Phoenix |
| Arkansas | Little Rock |
| California | Sacramento |
| … | … |
We'll say "the procedure f" when we want to discuss the operations
we're telling Scheme to carry out. We'll say "the function represented by
f" when our attention is focused on the value returned, rather than
on the mechanism. (But we'll often abbreviate that lengthy second phrase
with "the function f" unless the context is especially
confusing.)[2]
"It's long," said the Knight, "but it's very, very beautiful. Everybody that hears me sing it—either it brings the tears into their eyes, or else—"
"Or else what?" said Alice, for the Knight had made a sudden pause.
“Or else it doesn't, you know. The name of the song is called ‘Haddock's Eyes.’ ”
"Oh, that's the name of the song, is it?" Alice said, trying to feel interested.
"No, you don't understand," the Knight said, looking a little vexed. “That's what the name is called. The name really is ‘The Aged Aged Man.&rsquo ”
“Then I ought to have said ‘That's what the song is called’?” Alice corrected herself.
“No, you oughtn't; that's quite another thing! The song is called &lsquoWays And Means&rsquo: but that's only what it's called, you know!”
"Well, what is the song, then?" said Alice, who was by this time completely bewildered.
"I was coming to that," the Knight said. “The song really is &lsquoA-sitting On A Gate’: and the tune's my own invention.”
Lewis Carroll, Through the Looking-Glass, and What Alice Found There
Notice that when we defined the square procedure we gave a name, x, for its argument. By contrast, when we invoked
square we provided a value for the argument (e.g., 7).
The word x is a "place holder" in the definition that stands for
whatever value you use when you call the procedure. So you can read the
definition of square as saying, "In order to square a number,
multiply that number by that number." The name x
holds the place of the particular number that you mean.
Be sure you understand this distinction between defining a procedure and
calling it. A procedure represents a general technique that can be applied
to many specific cases. We don't want to build any particular case into the
procedure definition; we want the definition to express the general nature of
the technique. You wouldn't want a procedure that only knew how to take the
square of 7. But when you actually get around to using square, you have
to be specific about which number you're squaring.
The name for the name of an argument (whew!) is formal parameter. In our square example, x
is the formal parameter. (You may hear people say either "formal"
alone or "parameter" alone when they're feeling lazy.) The
technical term for the actual value of the argument is the actual argument. In a case like
(square (+ 5 9))
you may want to distinguish the actual argument expression (+ 5 9) from the actual argument value 14. Most of the time it's perfectly clear
what you mean, and you just say "argument" for all of these things, but
right now when you're learning these ideas it's important to be able to talk
more precisely.
The square procedure takes one argument. If a procedure requires more
than one argument, then the question arises, which actual argument goes with
which formal parameter? The answer is that they go in the order in which
you write them, like this:
(define (f a b) (+ (* 3 a) b)) > (f 5 8) 23 > (f 8 5) 29
What's the average of 17 and 25? To answer this question you could add the two numbers, getting 42, and divide that by two, getting 21. You could ask Scheme to do this for you:
> (/ (+ 17 25) 2) 21
What's the average of 14 and 68?
> (/ (+ 14 68) 2) 41
Once you understand the technique, you could answer any such question by typing an expression of the form
(/ (+ ______ ______ ) 2)
to Scheme.
But if you're going to be faced with more such problems, an obvious next step is to generalize the technique by defining a procedure:
(define (average a b) (/ (+ a b) 2))
With this definition, you can think about the next problem that comes along in terms of the problem itself, rather than in terms of the steps required for its solution:
> (average 27 4) 15.5
This is an example of what we meant when we defined "abstraction" as noticing a pattern and giving it a name. It's not so different from the naming of such patterns in English; when someone invented the name "average" it was, probably, after noticing that it was often useful to find the value halfway between two other values.
This naming process is more important than it sounds, because once we have a name for some idea, we can use that idea without thinking about its pieces. For example, suppose that you want to know not only the average of some numbers but also a measure of whether the numbers are clumped together close to the average, or widely spread out. Statisticians have developed the "standard deviation" as a measure of this second property. You'd rather not have to think about this mysterious formula:
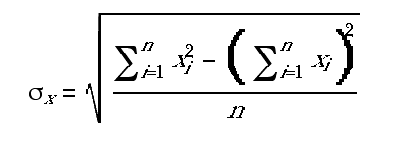
but you'd be happy to use a procedure standard-deviation
that you found in a collection of statistical programs.
After all, there's no law of nature that says computers automatically know
how to add or subtract. You could imagine having to instruct Scheme to
compute the sum of two large numbers digit by digit, the way you did in
elementary school. But instead someone has "taught" your computer how to
add before you get to it, giving this technique the name + so that you
can ask for the sum of two numbers without thinking about the steps required.
By inventing average or standard-deviation we are extending the
repertoire of computations that you can ask for without concerning yourself
with the details.
We've suggested that a procedure you define, such as average, is
essentially similar to one that's built into Scheme, such as +.
In particular, the rules for building expressions are the same whether
the building blocks are primitive procedures or defined procedures.
> (average (+ 10 8) (* 3 5)) 16.5 > (average (average 2 3) (average 4 5)) 3.5 > (sqrt (average 143 145)) 12
Any return value can be used as an end in itself, as the return
value from sqrt was used in the last of these examples, or it can
provide an argument to another procedure, as the return value from
* was used in the first of these examples.
These small examples may seem arbitrary, but the same idea, composition of
functions, is the basis for all Scheme programming. For example, the
complicated formula we gave for standard deviation requires computing the
squares of several numbers. So if we were to write a standard-deviation procedure, it would invoke square.
We've paid a lot of attention to the details of formal parameters and actual arguments, but we've been a little handwavy[3] about how a procedure actually computes a value when you invoke it.
We're going to explain what happens when you invoke a user-defined procedure. Every explanation is a story. No story tells the entire truth, because there are always some details left out. A model is a story that has just enough detail to help you understand whatever it's trying to explain but not so much detail that you can't see the forest for the trees.
Today's story is about the substitution model. When a
procedure is invoked, the goal is to carry out the computation described in
its body. The problem is that the body is written in terms of the formal
parameters, while the computation has to use the actual argument values. So
what Scheme needs is a way to associate actual argument values with formal
parameters. It does this by making a new copy of the body of the procedure,
in which it substitutes the argument values for every appearance of the
formal parameters, and then evaluating the resulting expression. So, if
you've defined square with
(define (square x) (* x x))
then the body of square is (* x x). When you want to
know the square of a particular number, as in (square 5), Scheme
substitutes the 5 for x everywhere in the body of square and evaluates
the expression. In other words, Scheme takes
(* x x)
then does the substitution, getting
(* 5 5)
and then evaluates that expression, getting 25.
If you just type (* x x) into Scheme, you will get an error message
complaining that x doesn't mean anything. Only after the substitution
does this become a meaningful expression.
By the way, when we talk about "substituting into the body," we don't mean that the procedure's definition is changed in any permanent way. The body of the procedure doesn't change; what happens, as we said before, is that Scheme constructs a new expression that looks like the body, except for the substitutions.[4]
There are little people who specialize in square, just as there
are little people who specialize in + and *. The difference is
that the little people who do primitive procedures can do the work "in their
head," all at once. The little people who carry out user-defined procedures
have to go through this substitution business we're talking about here.
Then they hire other little people to help evaluate the resulting expression,
just as Alonzo hires people to help him evaluate the expressions you type
directly to Scheme.
Let's say Sam, a little person who specializes in square, has been
asked to compute (square 6). Sam carries out the substitution, and is
left with the expression (* 6 6) to evaluate. Sam then hires Tessa, a
multiplication specialist, to evaluate this new expression. Tessa tells Sam
that her answer is 36, and, because the multiplication is the entire problem
to be solved, this is Sam's answer also.
Here's another example:
(define (hypotenuse a b) (sqrt (+ (square a) (square b)))) > (hypotenuse 5 12)
Suppose Alonzo hires Harry to compute this expression.
Harry must first substitute the actual argument values (5 and 12) into the
body of hypotenuse:
(sqrt (+ (square 5) (square 12)))
Now he evaluates that expression, just as Alonzo would evaluate it
if you typed it at a Scheme prompt. That is, Harry hires four little
people: one sqrt expert, one + expert, and two square
experts.[5] In particular, some little
person has to evaluate (square 5), by substituting 5 for x in
the body of square, as in the earlier example. Similarly, we
substitute 12 for x in order to evaluate (square 12):
(hypotenuse 5 12) ; substitute into HYPOTENUSE body
(sqrt (+ (square 5) (square 12))) ; substitute for (SQUARE 5)
(* 5 5)
25
(sqrt (+ 25 (square 12))) ; substitute for (SQUARE 12)
(* 12 12)
144
(sqrt (+ 25 144))
(+ 25 144) ; combine the results as before
169
(sqrt 169)
13
Don't forget, in the heady rush of learning about the substitution model, what you already knew from before: Each piece of this computation is done by a little person, and some other little person is waiting for the result. In other words, the substitution model tells us how each compound procedure is carried out, but doesn't change our picture of the way in which procedure invocations are composed into larger expressions.
Don't forget that a function can have only one return value. For example, here's a program that's supposed to return the sum of the squares of its two arguments:
(define (sum-of-squares x y) ;; wrong! (square x) (square y))
The problem is that the body of this procedure has two expressions, instead of just one. As it turns out, Scheme just ignores the value of the first expression in cases like this, and returns the value of the last one. What the programmer wants is the sum of these two values, so the procedure should say
(define (sum-of-squares x y)
(+ (square x)
(square y)))
Another pitfall comes from thinking that a procedure call changes the value of a parameter. Here's a faulty program that's supposed to compute the function described by f(x)=3x+10:
(define (f x) ;; wrong! (* x 3) (+ x 10))
Again, the first expression has no effect and Scheme will just return the value x+10.[6]
A very common pitfall in Scheme comes from choosing the name of a procedure as a parameter. It doesn't come up very often with procedures like the ones in this chapter whose domains and ranges are both numbers, but it will be more likely later. If you have a program like this:
(define (square x) (* x x)) (define (area square) ;; wrong! (square square))
then you'll get in trouble when you invoke the procedure, for
example, by saying (area 8). The area little person will
substitute 8 for square everywhere in the procedure definition,
leaving you with the expression (8 8) to evaluate. That expression
would mean to apply the procedure 8 to the argument 8, but
8 isn't a procedure, so an error message results.
It isn't a problem if the formal parameter is the name of a procedure that
you don't use inside the body. The problem arises when you try to use the
same name, e.g., square, with two meanings within a single procedure.
But special forms are an exception; you can never use the name of a special
form as a parameter.
A similar problem about name conflicts comes up if you try to
use a keyword (the name of a special form, such as define) as
some other kind of name—either a formal parameter or the name of a
procedure you're defining. We're listing this separately because the
result is likely to be different. Instead of getting the wrong value
substituted, as above, you'll probably see a special error message
along the lines of "improper use of keyword."
Formal parameters must be words. Some people try to write procedures that have compound expressions as the formal parameters, like this:
(define (f (+ 3 x) y) ;; wrong! (* x y))
Remember that the job of the procedure definition is only to provide a name for the argument. The actual argument isn't pinned down until you invoke the procedure. People who write programs like the one above are trying to make the procedure definition do some of the job of the procedure invocation.
4.1 Consider this procedure:
(define (ho-hum x y) (+ x (* 2 y)))
Show the substitution that occurs when you evaluate
(ho-hum 8 12)
4.2 Given the following procedure:
(define (yawn x) (+ 3 (* x 2)))
list all the little people that are involved in evaluating
(yawn (/ 8 2))
(Give their names, their specialties, their arguments, who hires them, and what they do with their answers.)
4.3 Here are some procedure definitions. For each one, describe the function in English, show a sample invocation, and show the result of that invocation.
(define (f x y) (- y x))
(define (identity x) x)
(define (three x) 3)
(define (seven) 7)
(define (magic n)
(- (/ (+ (+ (* 3 n)
13)
(- n 1))
4)
3))
4.4 Each of the following procedure definitions has an error of some kind. Say what's wrong and why, and fix it:
(define (sphere-volume r) (* (/ 4 3) 3.141592654) (* r r r)) (define (next x) (x + 1)) (define (square) (* x x)) (define (triangle-area triangle) (* 0.5 base height)) (define (sum-of-squares (square x) (square y)) (+ (square x) (square y)))
4.5 Write a procedure to convert a temperature from Fahrenheit to Celsius, and another to convert in the other direction. The two formulas are F=9⁄5C+32 and C=5⁄9(F-32).
4.6 Define a procedure fourth that computes the fourth power of its
argument. Do this two ways, first using the multiplication function,
and then using square and not (directly) using multiplication.
4.7 Write a procedure that computes the absolute value of its argument by finding the square root of the square of the argument.
4.8 "Scientific notation" is a way to represent very small or very large
numbers by combining a medium-sized number with a power of 10. For example,
5×107 represents the number 50000000, while 3.26×10-9
represents 0.00000000326 in scientific notation. Write a procedure
scientific that takes two arguments, a number and an exponent of 10,
and returns the corresponding value:
> (scientific 7 3) 7000 > (scientific 42 -5) 0.00042
Some versions of Scheme represent fractions in a/b form, and
some use scientific notation, so you might see 21/50000 or 4.2E-4
as the result of the last example instead of 0.00042, but these are
the same value.
(A harder problem for hotshots: Can you write procedures that go in the other direction? So you'd have
> (sci-coefficient 7000) 7 > (sci-exponent 7000) 3
You might find the primitive procedures log and floor helpful.)
4.9 Define a procedure discount that takes two arguments: an item's
initial price and a percentage discount. It should return the new price:
> (discount 10 5) 9.50 > (discount 29.90 50) 14.95
4.10 Write a procedure to compute the tip you should leave at a restaurant. It
should take the total bill as its argument and return the amount of the
tip. It should tip by 15%, but it should know to round up so that the
total amount of money you leave (tip plus original bill) is a whole number
of dollars. (Use the ceiling procedure to round up.)
> (tip 19.98) 3.02 > (tip 29.23) 4.77 > (tip 7.54) 1.46
(define (square x) &hellip) is the special form; the word define itself is called a keyword. But in fact Lispians are
almost always loose about this distinction and say "define is a
special form," just as we've done here. The word "form" is an archaic
synonym for "expression," so "special form" just means "special
expression."[2] Also, we'll sometimes use the terms "domain" and "range" when we're talking about procedures, although technically, only functions have domains and ranges.
[3] You know, that's when you wave your hands around in the air instead of explaining what you mean.
[4] You may be thinking that this is rather an inefficient way to do things—all this copying and replacement before you can actually compute anything. Perhaps you're afraid that your Scheme programs will run very slowly as a result. Don't worry. It really happens in a different way, but the effect is the same except for the speed.
[5] Until we started defining our own procedures in this
chapter, all of the little people were hired by Alonzo, because all
expressions were typed directly to a Scheme prompt. Now expressions can
come from the bodies of procedures, and so the little people needed to
compute those expressions are hired by the little person who's computing
that procedure. Notice also that each little person reports to
another little person, not necessarily the one who hired her. In
this case, if Harry hires Shari for sqrt, Paul for +, and Slim
and Sydney for the two squares, then Slim reports to Paul, not to
Harry. Only Shari reports directly to Harry.
[6] This is especially problematic for people
who used to program in a language like Pascal or BASIC, where you say things
like "X = X * 3" all the time.
Brian Harvey,
bh@cs.berkeley.edu