
|
|
The interaction between you and Scheme is called the "read-eval-print loop." Scheme reads what you type, evaluates it, and prints the answer, and then does the same thing over again. We're emphasizing the word "evaluates" because the essence of understanding Scheme is knowing what it means to evaluate something.
Each question you type is called an expression.[1] The
expression can be a single value, such as 26, or something more
complicated in parentheses, such as (+ 14 7). The first kind of
expression is called an atom (or atomic expression), while the second kind of expression is
called a compound expression, because it's made out of the
smaller expressions +, 14, and 7. The metaphor is from
chemistry, where atoms of single elements are combined to form chemical
compounds. We sometimes call the expressions within a compound expression
its subexpressions.
Compound expressions tell Scheme to "do" a procedure. This idea is so important that it has a lot of names. You can call a procedure; you can invoke a procedure; or you can apply a procedure to some numbers or other values. All of these mean the same thing.
If you've programmed before in some other language, you're probably accustomed to the idea of several different types of statements for different purposes. For example, a "print statement" may look very different from an "assignment statement." In Scheme, everything is done by calling procedures, just as we've been doing here. Whatever you want to do, there's only one notation: the compound expression.
Notice that we said a compound expression contains expressions. This means that you can't understand what an expression is until you already understand what an expression is. This sort of circularity comes up again and again and again and again[2] in Scheme programming. How do you ever get a handle on this self-referential idea? The secret is that there has to be some simple kind of expression that doesn't have smaller expressions inside it—the atomic expressions.
It's easy to understand an expression that just contains one number. Numbers are self-evaluating; that is, when you evaluate a number, you just get the same number back.
Once you understand numbers, you can understand expressions that add up numbers. And once you understand those expressions, you can use that knowledge to figure out expressions that add up expressions-that-add-up-numbers. Then and so on. In practice, you don't usually think about all these levels of complexity separately. You just think, "I know what a number is, and I know what it means to add up any expressions."
So, for example, to understand the expression
(+ (+ 2 3) (+ 4 5))
you must first understand 2 and 3 as self-evaluating
numbers, then understand (+ 2 3) as an expression that adds those
numbers, then understand how the sum, 5, contributes to the overall
expression.
By the way, in ordinary arithmetic you've gotten used to the idea that parentheses can be optional; 3+4×5 means the same as 3+(4×5). But in Scheme, parentheses are never optional. Every procedure call must be enclosed in parentheses.
You may not have realized it, but inside your computer there are thousands of little people. Each of them is a specialist in one particular Scheme procedure. The head little person, Alonzo, is in charge of the read-eval-print loop.
When you enter an expression, such as
(- (+ 5 8) (+ 2 4))
Alonzo reads it, hires other little people to help him evaluate
it, and finally prints 7, its value. We're going to focus on the
evaluation step.
Three little people work together to evaluate the expression: a minus person
and two plus people. (To make this account easier to read, we're using the
ordinary English words "minus" and "plus" to refer to the procedures
whose Scheme names are - and +. Don't be confused by this and
try to type minus to Scheme.)
Since the overall expression is a subtraction, Alonzo hires Alice, the first available minus specialist. Here's how the little people evaluate the expression:
| • | Alice wants to be given some numbers, so before she can do any work, she complains to Alonzo that she wants to know which numbers to subtract. |
|---|
| • | Alonzo looks at the subexpressions that should provide Alice's
arguments, namely, (+ 5 8) and (+ 2 4). Since both of these are
addition problems, Alonzo hires two plus specialists, Bernie and Cordelia,
and tells them to report their results to Alice.
|
|---|
| • | The first plus person, Bernie, also wants some numbers, so he asks Alonzo for them. |
|---|
| • | Alonzo looks at the subexpressions of (+ 5 8) that should provide
Bernie's arguments, namely, 5 and 8. Since these are both
atomic, Alonzo can give them directly to Bernie.
|
|---|
| • | Bernie adds his arguments, 5 and 8, to get 13. He
does this in his head—we don't have to worry about how he knows how to
add; that's his job.
|
|---|
| • | The second plus person, Cordelia, wants some arguments; Alonzo looks at
the subexpressions of (+ 2 4) and gives the 2 and 4 to
Cordelia. She adds them, getting 6.
|
|---|
| • | Bernie and Cordelia hand their results to the waiting Alice, who can now
subtract them to get 7. She hands that result to Alonzo, who prints
it.
|
|---|
How does Alonzo know what's the argument to what? That's what the grouping of subexpressions with parentheses is about. Since the plus expressions are inside the minus expression, the plus people have to give their results to the minus person.
We've made it seem as if Bernie does his work before Cordelia does hers. In fact, the order of evaluation of the argument subexpressions is not specified in Scheme; different implementations may do it in different orders. In particular, Cordelia might do her work before Bernie, or they might even do their work at the same time, if we're using a parallel processing computer. However, it is important that both Bernie and Cordelia finish their work before Alice can do hers.
The entire call to - is itself a single expression; it could be a
part of an even larger expression:
> (* (- (+ 5 8) (+ 2 4))
(/ 10 2))
35
This says to multiply the numbers 7 and 5, except that instead of
saying 7 and 5 explicitly, we wrote expressions whose values are 7 and 5.
(By the way, we would say that the above expression has three
subexpressions, the * and the two arguments. The argument
subexpressions, in turn, have their own subexpressions. However, these
sub-subexpressions, such as (+ 5 8), don't count as
subexpressions of the whole thing.)
We can express this organization of little people more formally. If an expression is atomic, Scheme just knows the value.[3] Otherwise, it is a compound expression, so Scheme first evaluates all the subexpressions (in some unspecified order) and then applies the value of the first one, which had better be a procedure, to the values of the rest of them. Those other subexpressions are the arguments.
We can use this rule to evaluate arbitrarily complex expressions, and Scheme won't get confused. No matter how long the expression is, it's made up of smaller subexpressions to which the same rule applies. Look at this long, messy example:
> (+ (* 2 (/ 14 7) 3)
(/ (* (- (* 3 5) 3) (+ 1 1))
(- (* 4 3) (* 3 2)))
(- 15 18))
13
Scheme understands this by looking for the subexpressions of the overall expression, like this:
(+ ()
( ; One of them takes two lines but you can tell by
) ; matching parentheses that they're one expression.
())
(Scheme ignores everything to the right of a semicolon, so semicolons can be used to indicate comments, as above.)
Notice that in the example above we asked + to add three
numbers. In the functions program of Chapter 2 we
pretended that every Scheme function accepts a fixed number of arguments,
but actually, some functions can accept any number. These include +,
*, word, and sentence.
Since a little person can't do his or her job until all of the necessary subexpressions have been evaluated by other little people, we can "fast forward" this process by skipping the parts about "Alice waits for Bernie and Cordelia" and starting with the completion of the smaller tasks by the lesser little people.
To keep track of which result goes into which larger computation, you can write down a complicated expression and then rewrite it repeatedly, each time replacing some small expression with a simpler expression that has the same value.
(+ (*(- 10 7)(+ 4 1)) (- 15 (/ 12 3)) 17) (+ (* 3(+ 4 1)) (- 15 (/ 12 3)) 17) (+(* 3 5 )(- 15 (/ 12 3)) 17) (+ 15 (- 15(/ 12 3)) 17) (+ 15(- 15 4 )17)(+ 15 11 17)43
In each line of the diagram, the boxed expression is the one that will be replaced with its value on the following line.
If you like, you can save some steps by evaluating several small expressions from one line to the next:
(+ (*(- 10 7)(+ 4 1)) (- 15(/ 12 3)) 17) (+(* 3 5 )(- 15 4 )17)(+ 15 11 17)43
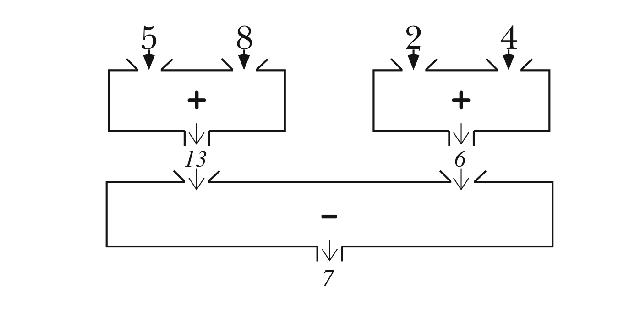
Some people find it helpful to look at a pictorial form of the connections among subexpressions. You can think of each procedure as a machine, like the ones they drew on the chalkboard in junior high school.
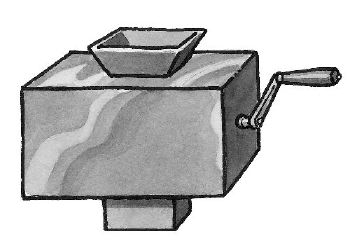
Each machine has some number of input hoppers on the top and one chute at the
bottom. You put something in each hopper, turn the crank, and something else
comes out the bottom. For a complicated expression, you hook up the output
chute of one machine to the input hopper of another. These combinations are
called "plumbing diagrams." Let's look at the plumbing diagram
for (- (+ 5 8) (+ 2 4)):
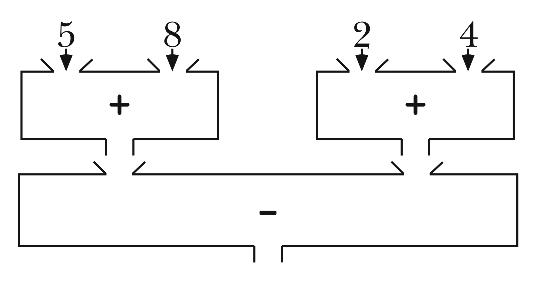
You can annotate the diagram by indicating the actual information that flows through each pipe. Here's how that would look for this expression:
One of the biggest problems that beginning Lisp programmers have comes from trying to read a program from left to right, rather than thinking about it in terms of expressions and subexpressions. For example,
(square (cos 3))
doesn't mean "square three, then take the cosine of
the answer you get." Instead, as you know, it means that the argument to
square is the return value from (cos 3).
Another big problem that people have is thinking that Scheme cares about the spaces, tabs, line breaks, and other "white space" in their Scheme programs. We've been indenting our expressions to illustrate the way that subexpressions line up underneath each other. But to Scheme,
(+ (* 2 (/ 14 7) 3) (/ (* (- (* 3 5) 3) (+ 1 1)) (- (* 4 3) (* 3 2))) (- 15 18))
means the same thing as
(+ (* 2 (/ 14 7) 3)
(/ (* (- (* 3 5) 3) (+ 1 1))
(- (* 4 3) (* 3 2)))
(- 15 18))
So in this expression:
(+ (* 3 (sqrt 49) ;; weirdly formatted (/ 12 4)))
there aren't two arguments to +, even though it looks that
way if you think about the indenting. What Scheme does is look at the
parentheses, and if you examine these carefully, you'll see that there are
three arguments to *: the atom 3, the compound expression (sqrt 49), and the compound expression (/ 12 4). (And there's only one
argument to +.)
A consequence of Scheme's not caring about white space is that when you hit the return key, Scheme might not do anything. If you're in the middle of an expression, Scheme waits until you're done typing the entire thing before it evaluates what you've typed. This is fine if your program is correct, but if you type this in:
(+ (* 3 4) (/ 8 2) ; note missing right paren
then nothing will happen. Even if you type forever, until
you close the open parenthesis next to the + sign, Scheme will still
be reading an expression. So if Scheme seems to be ignoring you, try typing
a zillion close parentheses. (You'll probably get an error message about
too many parentheses, but after that, Scheme should start paying attention
again.)
You might get into the same sort of trouble if you have a double-quote
mark (") in your program. Everything inside a pair of quotation marks
is treated as one single string. We'll explain more about
strings later. For now, if your program has a stray quotation mark, like
this:
(+ (* 3 " 4) ; note extra quote mark (/ 8 2))
then you can get into the same predicament of typing and having Scheme ignore you. (Once you type the second quotation mark, you may still need some close parentheses, since the ones you type inside a string don't count.)
One other way that Scheme might seem to be ignoring you comes from the
fact that you don't get a new Scheme prompt until you type in an expression
and it's evaluated. So if you just hit the return or enter key
without typing anything, most versions of Scheme won't print a new prompt.
3.1 Translate the arithmetic expressions (3+4)×5 and 3+(4×5) into Scheme expressions, and into plumbing diagrams.
3.2 How many little people does Alonzo hire in evaluating each of the following expressions:
(+ 3 (* 4 5) (- 10 4))
(+ (* (- (/ 8 2) 1) 5) 2)
(* (+ (- 3 (/ 4 2))
(sin (* 3 2))
(- 8 (sqrt 5)))
(- (/ 2 3)
4))
3.3 Each of the expressions in the previous exercise is compound. How many subexpressions (not including subexpressions of subexpressions) does each one have?
For example,
(* (- 1 (+ 3 4)) 8)
has three subexpressions; you wouldn't count (+ 3 4).
3.4 Five little people are hired in evaluating the following expression:
(+ (* 3 (- 4 7)) (- 8 (- 3 5)))Give each little person a name and list her specialty, the argument values she receives, her return value, and the name of the little person to whom she tells her result.
3.5 Evaluate each of the following expressions using the result replacement technique:
(sqrt (+ 6 (* 5 2))) (+ (+ (+ 1 2) 3) 4)
3.6 Draw a plumbing diagram for each of the following expressions:
(+ 3 4 5 6 7) (+ (+ 3 4) (+ 5 6 7)) (+ (+ 3 (+ 4 5) 6) 7)
3.7 What value is returned by (/ 1 3) in your version of
Scheme? (Some Schemes return a decimal fraction like 0.33333, while
others have exact fractional values like 1/3 built in.)
3.8 Which of the functions that you explored in Chapter 2 will accept variable numbers of arguments?
3.9 The expression (+ 8 2) has the value 10. It is a compound
expression made up of three atoms. For this problem, write five other
Scheme expressions whose values are also the number ten:
| • | An atom |
|---|
| • | Another compound expression made up of three atoms |
|---|
| • | A compound expression made up of four atoms |
|---|
| • | A compound expression made up of an atom and two compound subexpressions |
|---|
| • | Any other kind of expression |
|---|
[2] and again
[3] We'll explain this part in more detail later.
Brian Harvey,
bh@cs.berkeley.edu