Research Areas

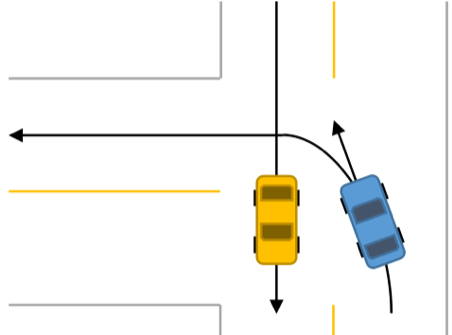Autonomous systems require mathematical tools that provide formal safety and performance guarantees with scalable computation. For formal guarantees we pursue an integrated design of the control stack, where different layers in the hierarchy (such as routing, planning, low-level control) account for each other. We employ appropriate notions of abstractions to distill relevant characteristics of one layer to be used in another, e.g., a finite state model suitable for real-time planning that captures all possible dynamical behaviors of the physical system. For scalability we use a combination of nonlinear systems methods and data-driven learning tools. An example of this combination is our approach to reachability analysis – an important ingredient for abstraction and safety guarantees – where we generate sample trajectories and expand the points reached by the samples to cover neighboring trajectories. For this expansion we use both nonlinear systems methods, such as monotone systems theory and contraction theory, and statistical learning concepts. In another line of work, we synthesize neural network controllers with a training scheme that guarantees stability, robustness, and performance. We pursue applications of these methods to self-driving cars, autonomous marine vessels, and vertical takeoff and landing aircraft.

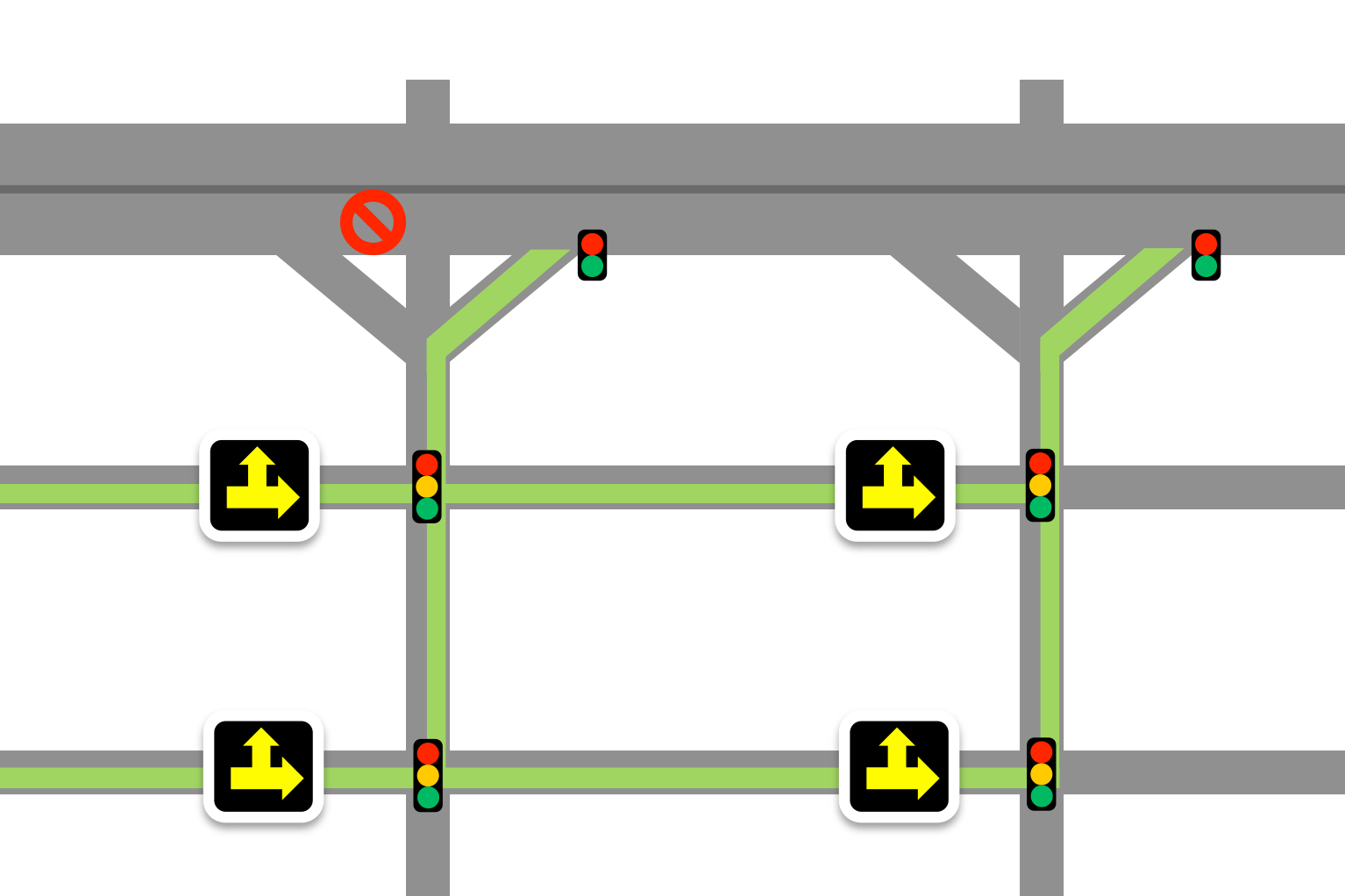Control of networks is invariably organized in layers, such as the vehicle, link, and network layers in vehicle traffic networks. We aim to make efficient use of the existing infrastructure by coordinating control actions across layers synergistically. At the vehicle layer we investigate how vehicle fleets can dramatically increase the capacity of urban roads and intersections by maintaining a constant spacing between them (see this video for an experimental demonstration). At the road link layer, we bring tools from formal methods to develop reactive signal timing policies for finite horizon objectives, such as dissipating queues and avoiding saturation. At the network layer we study routing games and account for the transient dynamics resulting from users’ revision of their route choices. A major goal of this study is to enable better response systems to assist local authorities in managing extreme demand, such as when entire counties have to be evacuated to protect the residents from a wildfire. The theoretical approach is broadly applicable to other networks and allows us to integrate users’ strategic behavior within dynamical network models.

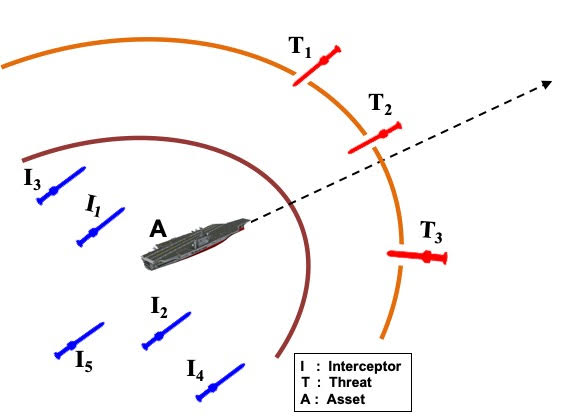In this research thread we develop scalable analysis and design tools for multi-agent systems, such as swarms of connected combat units, satellite constellations, power generation networks, and multicellular ensembles in biology. The multiplicity of agents enables applications with complex objectives and constraints that are not possible using individual systems. On the other hand, the combined dimension of the multi-agent system is typically beyond the reach of standard design methods. In one line of work we address this problem by extracting control-theoretic input-output properties from agent models and compose these properties to obtain network-level guarantees. In another line of work, we aggregate agents into fewer groups to cope with the large network size. Examples of such groups include generators that swing together in power systems and cells that exhibit similar fates in developmental biology. We further study optimal trajectory generation for multiple, heterogeneous agents for environmental monitoring (with combined use of satellites, drones, underwater vehicles) and defense applications (e.g., for guarding assets from multiple threats using a multi-interceptor system).