| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |
|
|
Program file for this chapter: math
Computer scientists often use mathematics as a tool in their work, but the mathematical problems that arise in computer science are of a special kind. Consider these examples:
Suppose you have a nondeterministic FSM with five states and you want to convert it to a deterministic one. What is the largest number of states that might be required for the new machine? Well, each state of the new machine corresponds to some combination of states of the old one, because the conversion works by finding multiple transitions (from some state via the same input character to multiple states) and creating a new state that combines all those resulting states. How many such combinations are possible? In other words, how many subsets does a five-element set have? The answer is 25 or 32 states. (31, really, because one of those is the empty subset and that will never be used.)
Suppose you want to write a program to translate telephone numbers into letters. A telephone number has seven digits, each of which corresponds to three letters. How many different strings of letters are possible? Well, there are three choices for the first digit, times three for the second, and so on...
These are typical of the kinds of mathematics problems that a computer
scientist confronts in that they are counting problems--ones that
involve integers. Another relevant kind of problem is the logic
problem, in which the values under consideration are just true and
false. These areas of mathematics are quite different from what is
studied in the usual high school and college math courses: algebra,
geometry, trig, calculus, differential equations. Those courses deal with
measurement problems, in which the answer can be any number,
including a fraction or an irrational number. This conventional mathematics
curriculum, studying continuous functions, is dictated by the needs
of physics and the physics-based engineering subjects. Computer scientists
need a different kind of math, called discrete mathematics.
("Discrete" is the opposite of "continuous" and is not the same word as
its homonym "discreet" meaning tactful.)
You already know that what in Logo is called an operation is the
computer programming version of a mathematical function. The inputs
and outputs of Logo operations may be numbers, or they may be other kinds of
words or lists. In ordinary algebra the functions we use have numeric
values. Certain Logo operations are identical to the ones used in algebra:
sin :x is sin(x) and sqrt :x is √x. On the other
hand, there is nothing in ordinary school mathematics quite like first
or sentence. You may have been taught to use the word "function"
only when you see a notation like f(x), but in fact the ordinary
arithmetic operations are functions, too. The addition in a+b is a
function with two arguments, just like sum :a :b in Logo.
In Logo there are also operations whose inputs and outputs are the words
true and false. The primitive operations in this category are
and, or, and not. Just as algebra deals with numeric
functions, logic is the branch of mathematics that deals with these
truth-valued functions. Instead of numbers, these functions combine
propositions: statements that may be true or false. A Logo
expression like :x=0 represents a proposition. "Abraham Lincoln was
the King of England" is a proposition; it happens to be false, but it's a
perfectly valid one because it asserts something that's either true or
false. "It will rain in Boston tomorrow" is a proposition whose truth
value we don't know yet. "Chinese food is better than French food" is an
example of a sentence whose validity as a proposition is open to question.
If I say that, I'm expressing my personal taste, not an objective statement
that could be proven true or false.*
*On the other hand, "The Beatles are better than Led Zeppelin" is a perfectly valid, obviously true proposition.
Logical functions combine simple propositions into compound propositions. For example, "Either Abraham Lincoln was the King of England or he was the President of the United States" is a compound proposition. It's true even though one of the simple propositions within it is false. Just as in algebra we use letters like x to represent numbers and expressions like x+y to indicate the use of functions to combine numbers, in logic we use letters to represent propositions and there are function symbols for the logical functions. If p is the proposition "Abraham Lincoln was the King of England," and q is the proposition "Abraham Lincoln was the President of the United States," then the expression p∨q represents the compound proposition above. The symbol ∨ represents the or function; ∧ represents and; ¬ and ∼ are alternative representations for not. The symbol → represents "implies"; it turns out that p→q is equivalent to ¬p∨q; in other words, the value of the function is true if either the "if" part is false or the "then" part is true. An example of the former is the classic "If wishes were horses then beggars would ride."
(Don't confuse the → function with the Logo if command. The
latter isn't a function (an operation), but a command. It tells Logo to
take some action if a given condition is met. The operation
to implies :p :q output or (not :p) :q end
is the Logo equivalent of the → function in logic.)
The most important use of logic in mathematics is in understanding the idea of proof. What is a valid reason for claiming that some proposition has been proven true? Many people come across the idea of proof for the first and last time in high school geometry. We are asked to prove some proposition like "the sum of the interior angles of a triangle is 180°." For each step in the proof we must give a reason such as "things equal to the same thing are equal to each other."
In logic there are certain rules that allow us to infer one proposition from one or more previously known propositions. These rules correspond roughly to the "reasons" in a geometry proof. They are called rules of inference. You use rules of inference informally all the time, whenever you try to convince someone of something by reasoning. "Is Jay here?" "Yes." "How do you know?" "I saw his car in the driveway, and if his car is here, he must be here too."
Suppose we use the letter p to represent the proposition "Jay's car is here" and the letter q to represent "Jay is here." Then the reasoning quoted in the last paragraph says "p is true and p→q is true, so q must be true." ("p→q" is the proposition "If Jay's car is here, he must be here too.") The fact that p and p→q allow us to infer q is a rule of inference. (Of course the rule doesn't tell us about the truth of its component propositions. We have to determine that by some means outside of logic, such as observation of the world. I had to see Jay's car in the driveway to know that p is true.)
What does all this have to do with computer science? One application of logic is in inference systems: programs that deduce propositions from other ones. Such systems are important both in business applications where large data bases are used and in artificial intelligence programs that try to answer questions based on information implied by some text but not explicit in the text.
In this section I'll show you a special-purpose inference system that solves logic problems. Logic problems are the ones in which you're given certain propositions and asked to deduce others. Mr. Smith lives next to the carpenter; John likes classical music; who lives in the yellow house? Here is a typical problem taken from Mind Benders, Book B-2, by Anita Harnadek.
On the first interview, he wrote these statements, one from each person:
1. Jane: "My name is Irving, and I'm 45." 2. King: "I'm Perry and I drive test cars." 3. Larry: "I'm a police sergeant and I'm 45." 4. Nathan: "I'm a drafter, and I'm 38." On the second interview, he wrote these statements, one from each person:
5. Mendle: "I'm a pilot, and my name is Larry." 6. Jane: "I'm a pilot, and I'm 45." 7. Opal: "I'm 55 and I drive test cars." 8. Nathan: "I'm 38 and I drive test cars."
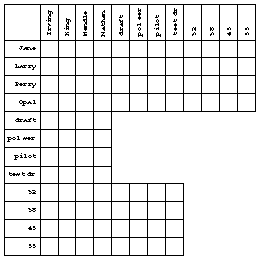
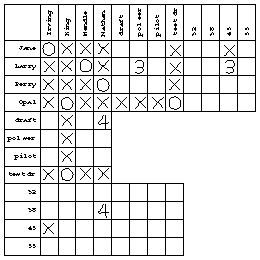
The chart provided with the problem is a guide to its solution. Each square in the chart represents a proposition. For example, the box where the "Larry" row meets the "pilot" column represents the proposition "Larry is the pilot." In solving the problem, you can put marks in the boxes to indicate what you know about the propositions. The status of a proposition need not be only true or false. Initially the status of each proposition is unknown; we have no idea whether it's true or false. The structure of this particular problem also allows the status of a proposition to be that it is linked with another proposition in an exclusive-or relationship; that is, if one of the linked propositions turns out to be true, then the other must be false, and vice versa. You can use whatever notation you find convenient to express these possibilities. After experimenting with T and F and with check marks and crosses, I found that circles for true propositions and crosses for false ones made it easiest for me to see quickly the pattern of known truths. For the linked propositions, I used the statement numbers (1 to 8) in the boxes; two boxes with the same number represent linked statements.
You should probably solve this problem by hand before we go on to discuss the computer solution. Stop reading now and work on the problem if you want to do it without any hints from me.
Let me introduce a little new terminology to help in the following discussion. I'll call something like "last name" or "occupation" a category; something like "Mendle" or "pilot" I'll call an individual. As I'm using this terminology, "Mendle" and "pilot" are two different individuals even if they turn out, when we solve the problem, to be the same person.
It's important that each group of four statements contains one from each person, because the names of the speakers include first and last names. That is, from the first group of statements we know that Jane, King, Larry, and Nathan are four distinct people. This falsifies such propositions as "Jane is King." After noting the first group of statements my chart looks like this:
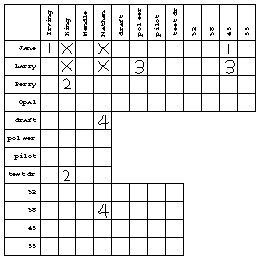
From the second group of statements we learn that Mendle, Jane, Opal, and Nathan are all distinct people. When I marked an X in the "Jane is Mendle" box, I noticed that all but one last name for Jane had been eliminated. I therefore put a circle in the "Jane is Irving" box. This illustrates a special rule of inference for problems of this kind: If, for a given individual x, all but one proposition "x is y" have been falsified for a certain category of y individuals, then the remaining proposition in that category must be true. (The reason I'm going through this analysis is that the rules of inference I discover while working the problem by hand are going to end up in the design of the computer program.) I'm going to call this the elimination rule.
Since Jane is Irving, nobody else can be Irving. This falsifies three propositions whose status was formerly unknown: "Larry is Irving," "Opal is Irving," and "Perry is Irving." (The truth of "Jane is Irving" would also falsify "Jane is King" and so on, but we already knew those to be false.) The general rule is that if "x is y" is true then "x is z" must be false for all other z in the same category as y, and likewise "w is y" is false for all other w in the same category as x. I'll call this the uniqueness rule.
The proposition "Jane is Irving" was linked with the proposition "Jane is 45" earlier. That latter proposition must therefore be false. This is another rule of inference, the link falsification rule. There is also a link verification rule that comes into play when a linked proposition is found to be false; the other linked proposition must then be true.
Since we know that "Jane is 45" is false, and that "Jane is Irving" is true, it follows that "Irving is 45" must be false. The general rule is that if "x is y" is true and "x is z" is false, then "y is z" must also be false. Similarly, if "x is y" is true and "x is z" is true, then "y is z" must be true. I'll call these the transitive rules.
You should be following along with your own copy of the chart. By the elimination rule, "Opal is King" must be true. Then, by the uniqueness rule, "Perry is King" is false. Then, by the link verification rule, "King is test driver" must be true. By the transitive rule, "Opal is test driver" is true also. Here is my chart after making all possible deductions from the fact that Mendle, Jane, Opal, and Nathan are distinct people:
Looking at statement number 5, we see that "Mendle is pilot" is linked to "Mendle is Larry." But we already know that the latter is true, so the former must be false. We can just put an X in that box and not bother marking the number 5 anywhere. The same is true for statements 6 and 7; here's my chart after statement 7:
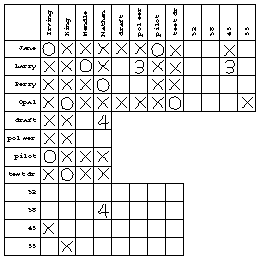
I haven't marked anything in the age vs. occupation section of the chart, even though I can deduce some propositions for that section. For example, I know that "Jane is pilot" is true and that "Jane is 45" is false. By the transitive rule, "pilot is 45" must be false. I just haven't bothered making all possible deductions; I can always fill in that section of the chart if I get to the end of the problem and still don't know who's who.
Before dealing with the final statement we know all the pairings of first and last names, but we don't know any ages and we only know half the jobs. The last statement lets loose a flurry of deductions. The critical one is that if Nathan is 38, he or she (Perry is an ambiguous first name) can't be the drafter because of the link from statement 4. Here is my final chart:
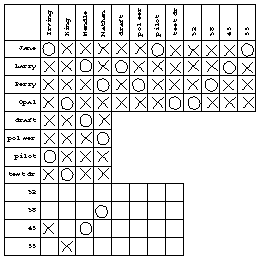
Once it was clear that I was in the final steps of the solution, I didn't bother maintaining the age vs. last name section. The results can be found by reading just the three sections at the top; for example, Jane is Irving, the pilot, and 55.
The elimination, uniqueness, and transitive rules are useful in just about all logic problems, but the link falsification and link verification rules depend on this specific problem's gimmick that we are given pairs of propositions and told that exactly one of them is true. To solve other problems, a more flexible kind of linkage is needed; we must be able to say "if p is true, then q is true also" or "if p is false, then q must be true," and so on.
A very common kind of linkage is an ordering, in which we are told a sequence of events, or a row of houses on a street, for example. In the cub reporter problem, the ages form an ordering, but aren't used as such--that is, the problem doesn't include clues such as "the test driver is younger than Jane." Suppose we did see that clue; what could we conclude from it? Certain propositions would be settled for sure:
| • | The test driver must not be Jane. | |
|---|---|---|
| • | The test driver isn't the oldest age (55). | |
| • | Jane isn't the youngest age (32). |
Other propositions would be linked by implications:
| • | If Jane is 38, then the driver is 32. | |
|---|---|---|
| • | If Jane is 45, then the driver is 32 or 38. |
and so on. (Actually, the second of these isn't directly representable on the chart, because there's no notation for a single proposition with two alternatives, like "32 or 38." So instead we'd represent this using propositions about what can't be true:
| • | If Jane is 45, then the driver is not 55. |
|---|
We already know that the driver isn't Jane, so there's no need to record the implication that if Jane is 45 the driver isn't 45.)
Here is another problem, called "Forgetful Footes," by Diane C. Baldwin. It is taken from The Dell Book of Logic Problems #4.
The forgetful Foote family fairly flew from their flat up Fleet Street to the freeway for a fling in Florida. Before they passed five intersections, Felix and the other four Footes found they each had forgotten something (including the food) and were forced back to their flat to fetch it. Each turnaround was made at a different street intersection, one of them at Field Street. From the following clues, can you figure out who forgot what and in what order, and find the order of the intersections on Fleet Street from the Foote's flat to the freeway?
1. The second turnaround began at the street following Flag Street and the street before Fred had to return to the flat. 2. The men were responsible for the return for the film, the turnaround at Fig Street, and the fifth trip back. 3. Fork Street followed the one where they returned to fetch the flashlight and preceded the one where a woman had them make their first turnaround. 4. The final trip back didn't begin at Frond Street, nor was it the one to fetch the fan. 5. Frank's forgetfulness turned them back one block and one return trip following Francine's. 6. One woman was the third to forget, while the other woman turned them back at Flag Street. 7. They returned for the fiddle just before the trip back that began at Frond Street and just following the one requested by Flo.
This problem includes two orderings. The order of the intersections with cross streets is not necessarily the same as the time order of the return trips. That is, the Footes might have gone four blocks before making their first turnaround, then gone only one block before the second return, and so on. In making a chart for this problem, I used the numbers 1-5 to represent the order of streets, and the ordinals 1st-5th to represent the time order of return trips. Clue 1, then, gives us this series of implications:
| • | If Flag Street is 1, then 2nd is 2. | |
|---|---|---|
| • | If Flag Street is 2, then 2nd is 3. | |
| • | If Flag Street is 3, then 2nd is 4.
| |
| • | If 2nd is 2, then Flag Street is 1. | |
| • | If 2nd is 3, then Flag Street is 2. | |
| • | If 2nd is 4, then Flag Street is 3.
| |
| • | If 2nd is 2, then Fred is 3. | |
| • | If 2nd is 3, then Fred is 4. | |
| • | If 2nd is 4, then Fred is 5.
| |
| • | If Fred is 3, then 2nd is 2. | |
| • | If Fred is 3, then 2nd is 3. | |
| • | If Fred is 5, then 2nd is 4. |
It may seem that there are some missing from this list. What if Flag Street is 4? But that can't happen (and I so marked the chart) because then 2nd would have to be 5, and that would make Fred 6, which is too far. But notice that we do have to include both directions of implication between any two propositions. The clue tells us that if Flag Street is 1, then 2nd is 2, and also that if 2nd is 2, then Flag Street is 1.
See if you can solve this problem, and then we'll talk about the Logo-based inference system.
In addition to the status of the "x is y" propositions, the program
needs to keep track of the categories, like "first name," and the
individuals within each category. This information is needed for the sake
of the elimination and uniqueness rules. I chose to have a global variable
named categories containing (for the cub reporter problem) the list
[first last age job]
Each of the elements of that list is the name of a variable
containing the individuals in that category; for example, :age is
the list
[32 38 45 55]
The status of the "is" propositions is kept in property lists associated with the names of individuals. For example, to indicate that the proposition "Jane is King" is false, the program carries out these two instructions:
pprop "Jane "King "false pprop "King "Jane "false
Both are necessary because we can't predict whether we're going to be figuring out something about Jane or something about King when we next need this information. Actually, the fact that the proposition is stored twice reflects another inference rule, one that's so obvious we don't think about it at all when solving these problems without using a computer: the symmetric rule says that if x is y, then y is x.
If a given property's value is the empty list, that means that the truth of
the proposition is unknown. (Remember that Logo property lists give the
empty list as the value of a property that you haven't defined explicitly,
so I don't have to predefine all possible properties.) The word true
means that the proposition is known to be true; the word false means
that it's known to be false. If the proposition is linked to other
propositions by implication, then the value of the property is a list
containing four-element implication lists. The first member of each
implication is true or false to indicate which value of this
proposition implies something about the other proposition. The next two
members are names of individuals, indicating which other proposition is
determined by this one. The fourth member is again true or
false, indicating whether that other proposition is implied to be true
or implied to be false.
For example, the statement "My name is Irving, and I'm 45" attributed to Jane is stored as the following two implications:
| • | Under Jane and Irving, the list [true Jane 45 false].
| |
|---|---|---|
| • | Under Jane and 45, the list [true Jane Irving false].
|
Although the data structure as described so far
contains all the necessary information, it
turned out to be convenient to include some redundant forms of the same
information. For example, the elimination rule and the uniqueness rule
require the program to find all the peers of an individual--the
other individuals in the same category. It would be possible to start with
:categories and search for the known individual in a category list,
but it was easier to give each individual a category property whose
value is the name of the category to which it belongs.
Similarly, the transitive rule needs to know all of the propositions
involving a particular individual that are known to be true, and all
those that are known to be false. This
information is implicit in the properties already described, but to simplify
the program each individual has a true property whose value is a list
of the other individuals known to be equal to this one, and a false
property whose value is a list of the others known to be different from
this one. For example, after
processing statement 7 we know that Jane is Irving and that Jane is the
pilot, but we don't know Jane's age. Therefore the property list for
Jane has a property whose name is true and whose value is the list
[Irving pilot]
and one whose name is false and whose value is
[King Mendle Nathan drafter sergeant driver]
Finally, it turned out that at the end of the program, in order to print out
the solutions, it was convenient to have, for each individual, properties
with a category as the name and an individual in that category as the value.
For example, since Jane's last name is Irving, Jane has a property
whose name is last and whose value is Irving.
I wanted to enter the problem as a series of assertions, each represented by a Logo instruction. That is, I wrote this procedure:
to cub.reporter cleanup category "first [Jane Larry Opal Perry] category "last [Irving King Mendle Nathan] category "age [32 38 45 55] category "job [drafter pilot sergeant driver] differ [Jane King Larry Nathan] says "Jane "Irving 45 says "King "Perry "driver says "Larry "sergeant 45 says "Nathan "drafter 38 differ [Mendle Jane Opal Nathan] says "Mendle "pilot "Larry says "Jane "pilot 45 says "Opal 55 "driver says "Nathan 38 "driver print [] solution end
(The first instruction erases any old property lists left over
from a previous logic problem; the last prints out the results.) I made
category, differ, and says print out their inputs when invoked,
so that you can watch the progress of the solution while it's being computed.
The procedures differ and says were designed to reflect the
terms in which this problem is presented, rather than the internal workings
of the inference system. That is, if you compare the problem statement with
this procedure, it's easy to see which instructions represent which clues,
even if you have no idea how the program will actually solve the problem!
Our task is to implement differ and says using propositional
logic.
There's an important difference between differ and says.
Differ gives us direct information about the truth or falsehood of some
simple propositions; specifically, we learn that several "x is y"
propositions are false. Says, on the other hand, gives us no
direct information about simple propositions; it tells us about
implications linking two such propositions.
First let's consider how differ works. The instruction
differ [Jane King Larry Nathan]
tells us that Jane is not King, Jane is not Larry, Jane is
not Nathan, King is not Larry, King is not Nathan, and Larry is not Nathan.
In effect, differ will carry out the instructions
falsify "Jane "King falsify "Jane "Larry falsify "Jane "Nathan falsify "King "Larry falsify "King "Nathan falsify "Larry "Nathan
There's no need to invoke falsify for the six cases with
inputs in the opposite order (such as the proposition that King is not Jane)
because, as we'll see, falsify knows about the symmetric rule and
will record those automatically. By the way, some of these six are
unnecessary because the two individuals have the same category and therefore
couldn't possibly be the same, such as Jane and Larry, both first names.
But falsify will catch these cases and return without doing anything.
Here's how differ actually carries out all those falsify
instructions:
to differ :list print (list "differ :list) foreach :list [differ1 ? ?rest] end to differ1 :a :them foreach :them [falsify :a ?] end
Falsify, and a similar procedure verify to assert the truth
of a proposition, are implemented in terms of the central procedure
about propositions, settruth:
to verify :a :b settruth :a :b "true end to falsify :a :b settruth :a :b "false end
Settruth takes three inputs, two individuals and a truth
value. It records the truth or falsehood of the proposition that :a
is :b, and uses the rules of inference I've described to derive
other propositions when possible.
to settruth :a :b :truth.value
if equalp (gprop :a "category) (gprop :b "category) [stop]
localmake "oldvalue get :a :b
if equalp :oldvalue :truth.value [stop]
if equalp :oldvalue (not :truth.value) ~
[(throw "error (sentence [inconsistency in settruth]
:a :b :truth.value))]
print (list :a :b "-> :truth.value)
store :a :b :truth.value
settruth1 :a :b :truth.value
settruth1 :b :a :truth.value
if not emptyp :oldvalue ~
[foreach (filter [equalp first ? :truth.value] :oldvalue)
[apply "settruth butfirst ?]]
end
to settruth1 :a :b :truth.value
apply (word "find not :truth.value) (list :a :b)
foreach (gprop :a "true) [settruth ? :b :truth.value]
if :truth.value [foreach (gprop :a "false) [falsify ? :b]
pprop :a (gprop :b "category) :b]
pprop :a :truth.value (fput :b gprop :a :truth.value)
end
If the two individuals are in the same category, settruth
does nothing. This is to allow for cases such as the example
falsify "Jane "Larry
as explained earlier. If the individuals are in different
categories, the next step is to find what information was previously
available about this proposition. If it was already known to be true
or false, and the truth value input in this call agrees with what was
known, then the program has merely generated some redundant information
and settruth stops. If the known value disagrees with the input
value, then something is wrong; the program has proven two contradictory
propositions. Generally this means that some clue has been represented
incorrectly in the program.
If the proposition was not already known to be true or false, then we
have some new information. After notifying the user by printing a
message, settruth
must store that fact. (Procedures get and store are an
interface to the property list primitives that implement the symmetric
rule.) The next step is to make any possible inferences using the
elimination, uniqueness, and transitive rules; this is done separately
for ":a is :b" and for ":b is :a" by two
calls to the subprocedure settruth1.
Settruth1 invokes either findtrue or findfalse
depending on the truth value. Because of the not in the
first instruction of settruth1, findtrue is called when we are
falsifying a proposition, and vice versa. This makes sense because of
the tasks of these procedures. If we are falsifying a proposition,
then the elimination rule comes into play, and we try to find a true
proposition. If we are verifying a proposition, then the uniqueness
rule lets us find several false propositions on the same row or
column of the chart. The next instructions in settruth1 implement
the transitive rule, looking at other individuals known to be the same
as, or different from, :a. The last two instructions maintain
the redundant information used for printing the results and for carrying
out the transitive rule.
The final instruction in settruth deals with implications. If we
already knew that p→q and now we're learning that p is true,
we can infer that q is true. (This is another rule of inference,
which I'll call the implication rule.)
Speaking of implications, we can now explore how the says procedure
produces and records implications. The instruction
says "Jane "Irving 45
establishes a relationship between the two propositions "Jane is Irving" and "Jane is 45." The relationship is that exactly one of them must be true; the name for this is exclusive or.
to says :who :what1 :what2 print (list "says :who :what1 :what2) xor :who :what1 :who :what2 end to xor :who1 :what1 :who2 :what2 implies :who1 :what1 "true :who2 :what2 "false implies :who1 :what1 "false :who2 :what2 "true end
Says is a special case of xor (a common abbreviation
for exclusive or) in which the two propositions are about a common
individual, Jane in the example. The xor procedure establishes
two implications, p → ¬ q and
¬ p → q. In other words,
if we learn that Jane is Irving, then we can infer that Jane is not 45;
if we learn that Jane is not Irving, we can infer that Jane is 45.
(These two implications are not equivalent to each other; in
general, one
might be true and the other false. But the exclusive or relationship
means that both are true.)
The implies procedure takes six inputs. The first three are for
one proposition and the others for the second proposition. For each
proposition, two inputs are individuals (call them x and y) and
the third is true or false. If true, then the
proposition is "x is y"; if false, the proposition is
"x is not y."
Yet another rule of inference comes into play here, the contrapositive rule. It says that if p→q is true, then so is ¬q → ¬p. Although these two implications are mathematically equivalent, we must enter both of them into our data structure because we might happen to discover that ¬q is true, and we'll look for relevant implications filed under q rather than under p.
to implies :who1 :what1 :truth1 :who2 :what2 :truth2 implies1 :who1 :what1 :truth1 :who2 :what2 :truth2 implies1 :who2 :what2 (not :truth2) :who1 :what1 (not :truth1) end
The first call to implies1 stores the implication
in the form given to us; the second call stores its contrapositive.
to implies1 :who1 :what1 :truth1 :who2 :what2 :truth2
localmake "old1 get :who1 :what1
if equalp :old1 :truth1 [settruth :who2 :what2 :truth2 stop]
if equalp :old1 (not :truth1) [stop]
if memberp (list :truth1 :who2 :what2 (not :truth2)) :old1 ~
[settruth :who1 :what1 (not :truth1) stop]
if memberp (list :truth1 :what2 :who2 (not :truth2)) :old1 ~
[settruth :who1 :what1 (not :truth1) stop]
store :who1 :what1 ~
fput (list :truth1 :who2 :what2 :truth2) :old1
end
The first three instructions in implies1 check for the
case in which we are told that p→q but we already know
either p or ¬p. If we already know p, then we can
derive that q is true. There's no need to store the implication,
because it is already serving its purpose, which is to allow us to
infer q. If we already know ¬p, then we can forget about
this implication, because it isn't going to do us any good. We can't
infer anything about q from this situation.
The next two instructions check for the situation in which we are told p→q but we already know that p→¬q. In that case, p must not be true, because if it were, we could infer two contradictory conclusions. Therefore, we can falsify the proposition p.
Finally, if none of these conditions is met, we add this implication to the (possibly empty) list of already known implications about p.
For another example of implications at work, here's the Logo program for the Foote problem:
to foote.family cleanup category "when [1st 2nd 3rd 4th 5th] category "name [Felix Fred Frank Francine Flo] category "street [Field Flag Fig Fork Frond] category "item [food film flashlight fan fiddle] category "position [1 2 3 4 5] print [Clue 1] justbefore "Flag "2nd :position justbefore "2nd "Fred :position print [Clue 2] male [film Fig 5th] print [Clue 3] justbefore "flashlight "Fork :position justbefore "Fork "1st :position female [1st] print [Clue 4] falsify "5th "Frond falsify "5th "fan print [Clue 5] justbefore "Francine "Frank :position justbefore "Francine "Frank :when print [Clue 6] female [3rd Flag] print [Clue 7] justbefore "fiddle "Frond :when justbefore "Flo "fiddle :when print [] solution end
I've included print instructions to let the user know when the
program reaches each of the seven numbered clues. Clue 4 tells us
directly that two possible pairings of individuals are false, and
the program reflects this with two invocations of falsify. But
the other clues either tell us about the sex of the family members
or tell us that certain individuals are next to each other in an
ordering. The procedures male, female, and justbefore
reflect the language of the problem in the same way that says
reflected the language of the other problem.
to male :stuff differ sentence :stuff [Francine Flo] end to female :stuff differ sentence :stuff [Felix Fred Frank] end
Needless to say, this implementation of male and female
works only for this specific logic problem! It's tempting to try to
use the more general category mechanism this way:
category "sex [male female] verify "Francine "female verify "Flo "female verify "Felix "male verify "Fred "male verify "Frank "male
but unfortunately the structure of this inference system requires that each individual can only match one individual in another category; once we've verified that Francine is female, the uniqueness rule will deduce that Flo isn't female!
On the other hand, I've tried to write justbefore in a way
that will work for future problems.
to justbefore :this :that :lineup falsify :this :that falsify :this last :lineup falsify :that first :lineup justbefore1 :this :that :lineup end to justbefore1 :this :that :slotlist if emptyp butfirst :slotlist [stop] equiv :this (first :slotlist) :that (first butfirst :slotlist) justbefore1 :this :that (butfirst :slotlist) end to equiv :who1 :what1 :who2 :what2 implies :who1 :what1 "true :who2 :what2 "true implies :who2 :what2 "true :who1 :what1 "true end
The input named lineup is a list of individuals from
an ordering, in the correct order. In this problem, it will be the list
[1 2 3 4 5]
if the clue is about street position, or
[1st 2nd 3rd 4th 5th]
if the clue is about the order of events in time. As I explained when talking about orderings earlier, the instruction
justbefore "Flag "2nd :position
results in falsifying some propositions:
falsify "Flag "2nd falsify "Flag 5 falsify "2nd 1
and also asserts some implications:
implies "Flag 1 "true "2nd 2 "true implies "2nd 2 "true "Flag 1 "true implies "Flag 2 "true "2nd 3 "true implies "2nd 3 "true "Flag 2 "true implies "Flag 3 "true "2nd 4 "true implies "2nd 4 "true "Flag 3 "true implies "Flag 4 "true "2nd 5 "true implies "2nd 5 "true "Flag 4 "true
This inference system can solve many logic problems, but sometimes it
runs into trouble. I've already mentioned, while discussing the male
and female procedures, that the program insists that each individual
in a category must appear exactly once in the solution. Suppose you have
a problem about five people living in five houses; they have five distinct
first names, five last names, five occupations--but two of the houses
are yellow. It's sometimes possible to get around this, but the technique
is a little awkward. You can set up a category like this:
category "color [yellow1 yellow2 blue brown green]
then you find one clue that mentions a yellow house
and use yellow1 for that one:
verify "Fred "yellow1
but for any other mention of something being yellow in the problem, you represent that by saying that the individual is not one of the other colors:
differ "architect [blue brown green]
You never explicitly mention yellow2 except in setting
up the category.
That technique works if you know that yellow is the color that appears twice. What if the problem tells you only that there are five houses and four colors? Or what if some individuals are not in the solution? For example, a problem might discuss the activities of five people, each doing something on a different day of the week, but you don't know until you solve the problem which of the seven weekdays are involved.
An entirely different approach to solving logic problems by computer is backtracking. Instead of starting from the clues and making deductions, a program can start by making arbitrary guesses about who goes with what, and then use the clues to look for contradictions. If a contradiction is found, the program systematically makes a different guess until every possible arrangement has been tried. (Presumably before every possibility has been tried, one of them will not lead to a contradiction, and that's the solution.)
In practice, backtracking is a more flexible technique than the inference system I wrote, because it's easy to let a backtracking program try multiple appearances of an individual if the problem allows that. But I thought the inference system would be more interesting to study, for two reasons. First, the inference system more closely models the way people solve logic problems. In the cub reporter problem, with four people to keep straight, there are (4!)3 or 13,824 possible solutions. In the Foote problem, with five people, there are (5!)4 or just over 200 million possibilities. A computer can try them all, but a person couldn't.* (If multiple appearances were allowed, the numbers would be even higher.) Second, backtracking doesn't work at all unless the problem deals with a finite set of individuals, as in a logic problem. Inference systems can be generalized to deal with potentially unbounded problems.
*People do sometimes use a combination of inference and backtracking. If, by inference, you've established that Jane must be either the pilot or the drafter, but you can't settle which, you might decide to assume that Jane is the pilot and hope that you can then infer either a complete solution to the problem or a contradiction. In the latter case, you'd know that Jane must be the drafter.
The rules of inference in this program are specially designed for problems like the ones we've just solved. The implication rule is applicable to any propositional logic situation, but the ones based on categories, such as the uniqueness and elimination rules, are not. The idea of a "category" as we've used it isn't a general principle of logic; instead, that idea should really be expressed as a series of propositions. For example, to say "there is a category called `last name' whose members are Irving, King, Mendle, and Nathan" is really to make several statements of the form "Jane has exactly one last name," or, in terms of the basic "x is y" propositions,
| (Jane is Irving) ∨ (Jane is King) |
| ∨ (Jane is Mendle) ∨ (Jane is Nathan) |
and so on. If we wanted to solve this problem in a general inference system we'd assert the truth of all those propositions at the beginning. Then if the program discovers that Jane is Irving, it would have the two propositions
and
and from these it could infer
using the standard inference rules of propositional logic.
The "and so on" just above includes quite a large number of propositions.
And yet this small problem concerns a mere 16 individual names divided into
four categories. For a larger problem it would be nearly impossible to list
all the relevant propositions, and for a problem involving an infinite set
of individuals, such as the integers, it would be literally impossible. What
would make the representation of a problem easier is if we could use, in a
formal system, the same kind of language I used in describing (in English)
the inference rules earlier: "for all other z in the same category as
y..." There are two parts to such a formal notation. First, in addition
to the propositional variables like p used in propositional logic,
we need variables like x and y that can represent objects in the system
we want to describe. Second, we need a notation for "for all." The formal
system including these additions to propositional logic is called
predicate logic. The name is like that used in Logo to refer to
operations with true or false outputs because
the statements in predicate logic
involve truth-valued functions of objects analogous to the
Logo predicates. For example, the formula we've been representing
informally as "x is y" is represented formally using the
predicate function is(x,y). This
is much like the Logo expression
equalp :x :y
A predicate function of two arguments ("inputs" in Logo) is also called a relation in mathematics. Algebraic relations include ones like = (equal) and < (less than).
We are almost ready to show how the uniqueness rule can be expressed as a formula in predicate logic. If you're not accustomed to mathematical formalism, this formula is a little scary--perhaps the scariest thing in this book. But I want you to see it so that you'll appreciate the fact that just one formula of predicate logic can sum up a rule that would require many formulas in propositional logic. I'm going to introduce a new relation called "isa" that's true if its first argument is a member of its second argument. The first must be an individual and the second a category. For example, isa(pilot,job) is true. And the symbol ∀ means "for all." The uniqueness rule says that if x is y then x can't also be z for any z in the same category as y. Here's how to say that formally:
To indicate the linking of two propositions in the general inference system, no special rules of inference are required. To say "the reporter wrote down these two statements; one is true and the other false" is just to say p⊗q; I'm using the symbol ⊗ to represent the exclusive or function. This formula is equivalent to
A general inference system will know that if it's been told p⊗q and then later it learns, say, p then it can infer ¬q.
The cub reporter problem is simpler than some of its type in that the only relevant relation among individuals is "is," which is an equivalence relation. This means that if Jane is Irving then also Irving is Jane (the technical name for a relation with that property is symmetric), and also that if Jane is Irving, and Irving is the pilot, then Jane is the pilot (so the relation is transitive). It's relatively easy to work out all the implications of a proposition about equivalence relations.
By contrast, the Foote problem contains ordering relations like "is later than" that are transitive but not symmetric. To handle such problems the inference system must have a way to represent "x is the last." Other problems contain relations like "lives in the house next to" that are symmetric but not transitive. A statement like "Mr. Smith lives in the house at the end" has to be represented formally as something like "there is only one person x such that x lives in the house next to Mr. Smith."
One reason a general inference system is harder to program than the special-purpose one I've written in this chapter is that my system makes all possible inferences from any newly verified or falsified proposition. This is possible only because there is a finite, fairly small number of such inferences. Once you introduce variables and predicates, the number of possible inferences is potentially infinite. A general inference system must take care not to infer infinitely many useless results. One solution is to defer the making of inferences until the user of the system asks a question, and then infer only what's needed to answer that particular question. But it isn't always easy to know exactly what's needed.
An inference system like the one I'm vaguely describing is a central part of the programming language Prolog. In that language, you program not by issuing instructions that tell the computer what to do, but rather by making assertions that some proposition is true. You can then ask questions like "for what values of x is this formula true?"
Besides inference systems, another area in which logic is important in computer science is in the design of the computers themselves. In a computer, information is represented as electrical signals flowing through wires. (These days, a "wire" is likely to be a microscopic conducting region on a silicon chip rather than a visible strand of metal, but the principle is the same.) In almost all computers, each wire may be carrying one of two voltage levels at any moment. (It is the restriction to two possible voltages that makes them binary computers. It would be possible to build ternary computer circuits using three voltages, but I know of no practical application of that idea.) A computer is built out of small circuit elements called gates that combine or rearrange binary signals in various ways. Perhaps the simplest example of a gate is an inverter; it has one input signal and provides one output signal that is the opposite of the input. That is, if you have a high voltage coming into the inverter you get a low voltage out, and vice versa.
The voltages inside the computer can be thought of as representing numbers
(zeros and ones) or truth values (false and true). From now on I'll use the
symbols 0 and 1 to represent the voltages, but you can mentally replace 0
with false and 1 with true to see how what I'm saying here ties
in with what's gone before.
Suppose you have a gate with two input wires and one output. What are the possibilities for how that output is determined by the inputs? Each of the two inputs can have two possible values; that means that a gate has four different possible input configurations. For each of those four, the gate can output 0 or 1. As you can see from the chart below, this means that there are 16 possible kinds of two-input gates:
| input p: | 0 | 0 | 1 | 1 | |
|---|---|---|---|---|---|
| input q: | 0 | 1 | 0 | 1 | |
| outputs: | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | and (p∧q) | |
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 1 | 1 | 0 | exclusive or (p⊗q) | |
| 0 | 1 | 1 | 1 | or (p∨q) | |
| 1 | 0 | 0 | 0 | nor (not-or, ¬(p∨q)) | |
| 1 | 0 | 0 | 1 | equivalence (p↔q) | |
| 1 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | implies (p→q) | |
| 1 | 1 | 1 | 0 | nand (not-and, ¬(p∧q)) | |
| 1 | 1 | 1 | 1 |
The table indicates, for example, that a gate whose output is 1 only when both inputs are 1 is an and gate, implementing the usual logical and operation. The 16 possibilities include all the standard logic functions as well as several less obviously useful ones. Two gate types called nand and nor represent functions rarely used in mathematical logic but common in computer design because it is sometimes helpful to have the opposite of the signal you're logically interested in.
Numbers other than 0 and 1 can't be represented as a single signal in a single wire. That's why there isn't a "plus gate" along with the and gates, or gates, and so on; if both inputs to a plus gate were 1, the output would have to be 2. To add two zero-or-one numbers we need a more complicated device with two output wires, one of which is the "carry" to the next binary digit:
| A input: | 0 | 0 | 1 | 1 |
|---|---|---|---|---|
| B input: | 0 | 1 | 0 | 1 |
| sum out: | 0 | 1 | 1 | 0 |
| carry out: | 0 | 0 | 0 | 1 |
These sum and carry outputs can be defined in terms of logical operations:
| Sum | = | A⊗B |
| Carry | = | A∧B |
Exclusive or gates are, in fact, not generally used as basic hardware components, so this device is traditionally represented in terms of and gates, or gates, and inverters:
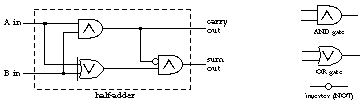
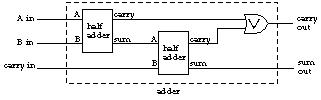
The device we've just built is called a half-adder for reasons that should become clear in a moment.
To represent numbers larger than 1 we have to use more than one signal wire. Each signal represents a binary digit, or bit, that is implicitly multiplied by a power of 2 just as in the ordinary decimal representation of numbers each digit is implicitly multiplied by a power of 10. For example, if we have three signal wires for a number, they have multipliers of 1, 2, and 4; with these signals we can represent the eight numbers from 0 (all signals 0) to 7 (all signals 1). When we want to add two such three-bit numbers, the sum for all but the rightmost bit can involve a carry in as well as a carry out. The circuit for each bit position must have three inputs, including one for the carry from the next bit over as well as the two external inputs. The outputs are found using these formulas:
| Sum | = | (A⊗B)⊗CarryIn |
| CarryOut | = | (A∧B)∨ ((A⊗B)∧CarryIn) |
This circuit can be built using two half-adders:
To add two three-bit numbers we connect three adders together this way:
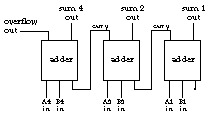
The carry out signal from the leftmost adder (the one representing the largest power of 2) is the overflow signal; if it's true, the sum didn't fit in the number of bits provided. Many computers use this signal to interrupt the execution of their programs so that people don't end up seeing incorrect results.
The phrase "computer logic" is widely used, even by non-experts, to refer to the inner workings of a computer. Many people, though, think that the phrase describes the personality of the computer, which they imagine to be like that of Mr. Spock. "Computers may be able to play chess, but they can't write poetry, because that isn't logical." Here you've seen the real meaning of the phrase: Just as a Logo program has procedures defined in terms of subprocedures and ultimately in terms of primitive procedures, the capabilities of a computer itself are built out of smaller pieces, and the primitive hardware components compute logical, rather than arithmetic, functions. (For a computer to exhibit Mr. Spock's sense of purpose, understanding of cause and effect, drive for self-preservation, loyalty to his species and his government, and so on, would be no less miraculous than for it to write a love poem or throw a temper tantrum. Later we'll discuss the efforts of artificial intelligence researchers to produce such miracles.)
Earlier I listed the 16 possible logical functions of two logical arguments. I could have figured out that there are 16 without actually listing them this way: If a function has two arguments, and each argument has two possible values, that makes 22 possible combinations of argument values. A logical function is determined by its result for each of those four possible argument combinations. (The four are f(0,0), f(0,1), f(1,0), and f(1,1).) There are two possible results for f(0,0), two for f(0,1), and so on; the number of possible functions is the product of all these twos, 222 or 16.
The mathematics of counting how things can be combined is called combinatorics. The problem we've just done illustrates a fundamental rule of combinatorics, namely that the number of possibilities for a choice with several components is the product of the number of possibilities for each component choice. This may be easier to understand with an example in which not all the relevant numbers are 2. Here's a classic: Suppose you have a group of four men and three women, and you want to form a committee of one man and one woman chosen from this group. How many such committees are possible? There are 4 choices for the male member of the committee and 3 choices for the female member; that means 4×3 or 12 committees.
(The multiplication rule only works if the component choices are independent; that is, the possible outcomes of one choice can't be affected by the outcome of any of the others. For example, if our committees are to have a chairperson who can be of either sex and then two other members, one man and one woman, you can't say "there are 7 choices for the chairperson, times 4 for the man, times 3 for the woman" because after choosing the chairperson the number of choices for the other members is changed depending on the sex of the chair. There are two correct ways to solve this problem. One is to say "The chairperson is either male or female. If male, there are 4 possible chairs, times 3 possible other male members, times 3 possible female members, for 36 possible committees. If female, there are 3 possible chairs, times 4 possible male members, times 2 possible other female members, for 24 committees. The total is 36+24 or 60 committees." The second solution is to pick the chairperson last; then you say "There are 4 possible male members, times 3 possible females, times 5 possible chairs (7 people in the original group minus 2 already chosen)." Apart from arithmetic errors, almost all the mistakes people make in solving combinatorics problems come from forgetting that events have to be independent to allow you to multiply the choices.)
Let's return to logical functions for a moment. Suppose we experiment with a ternary logic in which the possible values are yes, no, and maybe. (You can represent these using the numbers 0, 1, and 2.) How many three-argument ternary logic functions are there? Is it 3(33) or is it (33)3? (It doesn't matter which way you group the twos for the binary logic version because the two groupings have the same value, 16, but this isn't true with threes.) How many two-argument ternary logic functions are there? 2(32)? 3(23)? (33)2? How many three-argument binary logic functions? The virtue of these problems is that you can check your own answers by listing all the possible functions as I did for the two-argument binary logic functions.
Most people are introduced to combinatorics by way of probability, the mathematics of gambling. Given a number of equally likely possible situations, some of which win a bet and the rest of which lose it, the probability of winning is a ratio:
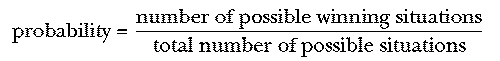
The role of combinatorics is to help in computing the numerator and denominator of that fraction.
For example, suppose you have six brown socks and four blue socks in a drawer, and you pull out two socks without looking. What is the probability of getting a matching pair? I'm going to give each sock a name like brown3 for the third brown sock so that we can talk about individual socks even if they're the same color. How many possible pairs of socks are there? That is, given the set
containing ten socks, how many two-sock subsets are there?
The first step in answering this question is to notice that we have 10 choices for the first sock and then 9 choices for the second. So there are 10×9 ways to make the two choices. (There is a subtle point here that some textbooks don't bother explaining. The choice of the second sock is not independent of the first choice, since we can't choose the same sock twice. However, the number of second choices is always 9, even though the particular nine available socks depend on the first choice. So we can get away with multiplying in this example.)
This isn't quite the answer we want, though. We've shown that there are 90 ordered pairs of socks. But once we get the socks out of the drawer, it doesn't matter which we picked first. In other words, if we say there are 90 possible choices, we are counting {brown2, brown5} and {brown5, brown2} as two different choices. Since we don't care which sock came out of the drawer first, we are really counting every pair twice, so there are only 90/2 or 45 possible pairs.
An ordered subset of a set is called a permutation; a subset without a particular order is a combination. We say that there are 90 permutations of ten things taken two at a time; there are 45 combinations of ten things taken two at a time.
It turns out that combinations are what matters most of the time; it's relatively rare for permutations to turn up in a math problem. An exception is the device wrongly called a "combination lock"; to open one, you must know a particular permutation of the possible numbers. My high school locker "combination" was 18-24-14. If I tried the same numbers in a different order, like 24-18-14, the lock wouldn't open. (Actually it's misleading for me to use this example because the same number can appear twice in most locks of this type, so the "combination" is not a subset of the available numbers. If there are 50 numbers available, the total number of possibilities is not 50×49×48 but rather 50×50×50. These lock-opening patterns are therefore neither permutations nor combinations but something else that we might call "permutations with repetition allowed.")
We haven't finished solving the sock problem. How many of the possible pairs of socks are matching pairs? One way to find out would be to list all the possible pairs and actually count how many of them match. This is the sort of thing computers do well. First we have to write a procedure that takes as input a list and a number, and outputs a list of lists, each of which is a subset of the input list whose length is the input number. That is, we want to take
combs [brown1 brown2 ... brown6 blue1 ... blue4] 2
and this should output a list of pairs:
[[brown1 brown2] [brown1 brown3] ... [brown4 blue3] ... [blue3 blue4]]
This is a fairly tricky program to write. Try it before you read further. Can you reduce the problem to a smaller, similar problem? Don't forget that we want combinations, not permutations, so the output can't have two sublists containing the same elements.
To make sure that each combination appears in the result in only one order,
we can decide explicitly what that order will be. The most convenient thing
is to say that the elements will appear in each sublist in the same order in
which they appear in the original list. That is, since the input list has
brown2 before blue3, the output will contain the list
[brown2 blue3]
but not the list
[blue3 brown2]
It follows that the very first element of the input list,
brown1, can only appear as the first element of any output sublist. In
other words, there are two kinds of sublists: ones with brown1 as
their first element and ones that don't include brown1 at all. This
is a way to divide the problem into smaller pieces.
If we are looking for n-element subsets, the first kind consists of
brown1 stuck in front of a smaller subset of n−1 elements chosen from the
remainder (the butfirst) of the input list. The second kind of subset
is an n-element subset of the butfirst. We can collect all of each
kind by a recursive invocation of the procedure we're going to write, then
append the two collections and output the result. So the procedure will
look like this:
to combs :list :howmany
... <stop rule> ...
output sentence (map [fput first :list ?]
combs (butfirst :list) (:howmany-1)) ~
(combs (butfirst :list) :howmany)
end
By now you've had a lot of experience writing
recursive procedures,
but I'm going over this one in detail for two reasons: It's tricky and it's a
model for solving many other combinatorial problems. What makes it tricky
is a combination of two things. One is that it's recursive twice; that is,
there are two recursive invocations of combs within combs. This
makes the control structure very different from the
to blah :list
output fput (something first :list) (blah butfirst :list)
end
sort of recursion that may be more familiar. The second tricky
part is that there are two input variables, each of which may be made smaller
(by butfirsting or by subtracting 1) but need not be in a particular
recursive call.
One implication of these complicating factors is that we need two
stop rules. It may be obvious that we need one for the situation of
counting :howmany down to zero, but we also need one for :list
getting too small. Ordinarily this latter would be an emptyp test, but
in fact any list whose length is less than :howmany is too small, not
just the empty list. Here is the finished procedure:
to combs :list :howmany
if equalp :howmany 0 [output [[]]]
if equalp :howmany count :list [output (list :list)]
output sentence (map [fput first :list ?]
combs (butfirst :list) (:howmany-1)) ~
(combs (butfirst :list) :howmany)
end
? show combs [a b c d e] 3
[[a b c] [a b d] [a b e] [a c d] [a c e] [a d e]
[b c d] [b c e] [b d e] [c d e]]
Now we can use combs on the sock problem. (Note: The procedure
socks shown here is not the one in the program file; there will be a
modified version a few paragraphs down the road.)
to socks :list
localmake "total combs :list 2
localmake "matching filter [equalp butlast first ? butlast last ?] ~
:total
print (sentence [There are] count :total [possible pairs of socks.])
print (sentence [Of these,] count :matching [are matching pairs.])
print sentence [Probability of match =] ~
word (100*(count :matching)/(count :total)) "%
end
? socks [brown1 brown2 brown3 brown4 brown5 brown6
blue1 blue2 blue3 blue4]
There are 45 possible pairs of socks.
Of these, 21 are matching pairs.
Probability of match = 46.6666667%
The answer is that the probability of a matching pair is just
under half. The template used in the invocation of filter in
socks depends on the fact that two socks match if their names are equal
except for the last character, such as brown3 and brown4.
I've numbered the socks because it's easier for us to talk about how the program works (and about how the underlying mathematics works, too) if we can identify an individual sock. But it's worth noting that the program doesn't really need individual sock names. We could instead use the list
[brown brown brown brown brown brown blue blue blue blue]
and change the filter template to
[equalp first ? last ?]
The program will generate some [brown brown] pairs, some
[brown blue] pairs, and some [blue blue] pairs. The number of
pairs will still be 45 and the number of matching pairs will still be 21.
Having come to that realization, we can make the "user interface" a little
smoother by having socks accept an input list like
[6 brown 4 blue]
and expand that into the desired list of ten socks itself. Here is the final program:
to socks :list
localmake "total combs (expand :list) 2
localmake "matching filter [equalp first ? last ?] :total
print (sentence [There are] count :total [possible pairs of socks.])
print (sentence [Of these,] count :matching [are matching pairs.])
print sentence [Probability of match =] ~
word (100*(count :matching)/(count :total)) "%
end
to expand :list
if emptyp :list [output []]
if numberp first :list ~
[output cascade (first :list)
[fput first butfirst :list ?]
(expand butfirst butfirst :list)]
output fput first :list expand butfirst :list
end
? socks [6 brown 4 blue]
There are 45 possible pairs of socks.
Of these, 21 are matching pairs.
Probability of match = 46.6666667%
My reason for presenting this refinement of the program is that it offers a concrete opportunity for reflection on how you can tell which differences are important in a combinatorics problem. In discussing the first version of the program, I said that the two lists
[brown2 brown5] and [brown5 brown2]
represent the same pair of socks, so both shouldn't be included in
the list of lists output by combs. Now I'm saying that several lists
that look identical like
[brown brown]
represent different pairs of socks and must all be counted. It would be a mistake to say, "There are three possibilities: brown-brown, brown-blue, and blue-blue. So the probability of a match is 2/3." It's true that there are three kinds of pairs of socks, but the three kinds are not equally represented in the list of 45 possible pairs.
The usual approach to problems like the one about the socks is not to enumerate the actual combinations, but rather to compute the number of combinations directly. There are formulas for both number of combinations and number of permutations. Usually the latter is derived first because it's easier to understand.
With 10 socks in the drawer, the number of two-sock permutations is 10×9. If we'd wanted three socks for a visiting extraterrestrial friend, the number of permutations would be 10×9×8. In general, if we have n things and we want to select r of them, the number of permutations is
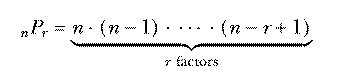
Mathematicians don't like messy formulas full of dots, so this is usually abbreviated using the factorial function. The notation "n!" is pronounced "n factorial" and represents the product of all the integers from 1 to n. Using this notation we can write
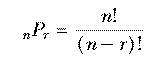
This is an elegant formula, but you should resist the temptation to use it as the basis for a computer program. If you write
to perms :n :r output (fact :n)/(fact (:n-:r)) end to fact :n output cascade :n [# * ?] 1 end
then you're doing more multiplications than necessary, plus an unnecessary division. Instead, go back to the earlier version in which r terms are multiplied:
to perms :n :r if :r=0 [output 1] output :n * perms :n-1 :r-1 end
The set of all permutations of n things taken r at a time includes several rearrangements of each combination of n things r at a time. How many rearrangements of each? Each combination is a set of r things, so the number of possible orderings of those r things is the number of permutations of r things r at a time, rPr or r!. nPr is greater than nCr, the number of combinations of n things taken r at a time, by this factor. In other words, if each combination corresponds to r! permutations, then the number of permutations is r! times the number of combinations. So we have
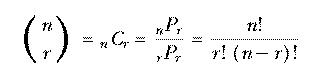
The notation 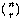 is much more commonly used in mathematics and
computer science texts than nCr. It's pronounced "n choose r."
is much more commonly used in mathematics and
computer science texts than nCr. It's pronounced "n choose r."
The traditional way to do the sock problem is this: The total number of
possible pairs of socks is 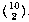 . The number of matching pairs is
equal to the number of brown pairs plus the number of blue pairs. The
number of brown pairs is the number of combinations of 6 brown socks chosen
2 at a time, or
. The number of matching pairs is
equal to the number of brown pairs plus the number of blue pairs. The
number of brown pairs is the number of combinations of 6 brown socks chosen
2 at a time, or 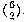 . Similarly, the number of pairs of blue socks
is
. Similarly, the number of pairs of blue socks
is 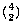 . So
. So
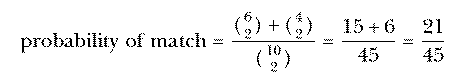
which is the same answer we got by enumerating and testing all the possible pairs.
A formula like
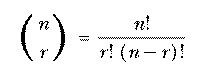
defines a mathematical function in terms of other, more elementary functions. It is comparable to a Logo procedure defined in terms of primitives, like
to second :thing output first butfirst :thing end
The "primitives" of mathematics are addition, subtraction, and so on, along with a few more advanced ones like the trigonometric and exponential functions. These are called "elementary functions" and a formula that defines some new function in terms of those is called a closed form definition.
The function 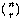 could also be defined in a different way based on
the ideas in the
could also be defined in a different way based on
the ideas in the combs program we used to enumerate combinations. The
combinations fall into two categories, those that include the first element
and those that don't. So the number of combinations is the sum of the
numbers in each category:
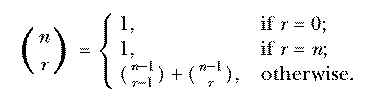
This is called an inductive definition. It is analogous to a recursive procedure in Logo.
These two formulas provide alternative definitions for the same
function, just as two Logo procedures can employ different algorithms but
have the same input-output behavior. How do we know that the two
definitions of 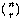 really do define the same function? Each
definition was derived from the fundamental definition of "the number of
combinations of n things taken r at a time" by different arguments.
If those arguments are correct, the two versions must define the same
function because there is just one correct number of combinations. It is
also possible to prove the two definitions equivalent by algebraic
manipulation; start with the closed form definition and see if it does, in
fact, obey the requirements of the inductive definition. For example, if
r=0 we have
really do define the same function? Each
definition was derived from the fundamental definition of "the number of
combinations of n things taken r at a time" by different arguments.
If those arguments are correct, the two versions must define the same
function because there is just one correct number of combinations. It is
also possible to prove the two definitions equivalent by algebraic
manipulation; start with the closed form definition and see if it does, in
fact, obey the requirements of the inductive definition. For example, if
r=0 we have
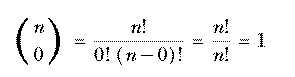
(It may not be obvious that 0! should be equal to 1, but mathematicians define the factorial function that way so that the formula n! = n·(n−1)! remains true when n=1.) See if you can verify the other two parts of the inductive definition. Here's a hint:
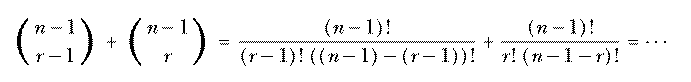
Why would anyone be interested in an inductive definition when the closed
form definition is mathematically simpler and also generally faster to
compute? There are two reasons. First, some functions don't have closed
form definitions in terms of elementary functions. For those functions,
there is no choice but to use an inductive definition. Second, sometimes
when you start with a non-formal definition of a function in terms of its
purpose, like "the number of combinations..." for 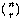 , it may be
easier to see how to translate that into an inductive definition as a first
step, even if it later turns out that there is also a less obvious closed
form. In fact, that's what I did in presenting the idea of combinations. I
found it more straightforward to understand the inductive definition because
it made sense to think about the actual combinations and not merely how many
of them there are. (In fact there is a mathematical technique called
generating functions that can sometimes be used to transform an
inductive definition into a closed form definition, but that technique
requires calculus and is beyond the scope of this book.)
, it may be
easier to see how to translate that into an inductive definition as a first
step, even if it later turns out that there is also a less obvious closed
form. In fact, that's what I did in presenting the idea of combinations. I
found it more straightforward to understand the inductive definition because
it made sense to think about the actual combinations and not merely how many
of them there are. (In fact there is a mathematical technique called
generating functions that can sometimes be used to transform an
inductive definition into a closed form definition, but that technique
requires calculus and is beyond the scope of this book.)
In addition to closed form and inductive definitions, it's often helpful to present a sort of partial definition of a function in the form of a table of values. (For logic functions, with only a finite number of possible values for the arguments of the function, such a table is actually a complete definition.) Partial definitions in a table of values can be particularly useful when the function displays some regularity that allows values outside the table to be computed easily based on the values in the table. For example, the sine function is periodic; its values repeat in cycles of 360 degrees. If you need to know the sine of 380 degrees, you can look up the sine of 20 degrees and that's the answer. For functions of two variables, like addition and multiplication, these function tables are often presented as square arrays of numbers. In elementary school you learned the addition and multiplication tables for numbers up to 10, along with algorithms for reducing the addition and multiplication of larger numbers to a sequence of operations on single digits.
The function 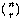 is a function of two variables, so it would
ordinarily be presented as a square table like the multiplication table,
except for the fact that this particular function is meaningfully defined
only when r≤n. (There are no combinations of three things taken five
at a time, for example, so
is a function of two variables, so it would
ordinarily be presented as a square table like the multiplication table,
except for the fact that this particular function is meaningfully defined
only when r≤n. (There are no combinations of three things taken five
at a time, for example, so 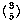 is 0.) So instead of a square
format like this:
is 0.) So instead of a square
format like this:
| r\n | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 0 | 1 | 3 | 6 | 10 |
| 3 | 0 | 0 | 0 | 1 | 4 | 10 |
| 4 | 0 | 0 | 0 | 0 | 1 | 5 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 |
this function is traditionally presented in a triangular form called
"Pascal's Triangle" after Blaise Pascal (1623-1662), who invented the
mathematical theory of probability along with Pierre de Fermat (1601-1665).
Pascal didn't invent the triangle, but he did pioneer its use in
combinatorics. Each row of the triangle contains the nonzero values of
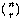 for a particular n:
for a particular n:
| 1 |
| 1 1 |
| 1 2 1 |
| 1 3 3 1 |
| 1 4 6 4 1 |
| 1 5 10 10 5 1 |
Pascal's Triangle is often introduced in algebra because the numbers in row n (counting from zero) are the binomial coefficients, the constant factors in the terms in the expansion of (a+b)n. For example,
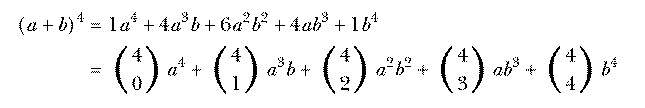
Do you see why the binomial coefficients are related to combinations? An
expression like (a+b)4 is a sum of products of four As and Bs. (How
many such products? Each term involves four choices between A and B;
there are 2 ways to make each choice, and the choices are independent, so
there are 24 possible products.) These products are combined into terms
based on the fact that some are equal to each other, such as aaab and
abaa, both of which contribute to the a3b term. How many arrangements
of three As and one B are there? That's like asking how many ways there
are to choose one slot for a B out of four possible slots, which is
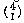 .
.
Can you predict what the coefficients will be in the expansion of (a+b+c)4? For example, what is the coefficient of ab2c? Try to multiply it out and see if your formula is right.
Everyone is taught in school that each number in Pascal's Triangle, except
for the 1s at the ends, is the sum of the two numbers above it. But this is
usually presented as a piece of magic with no explanation. It's not obvious
how that fact is connected to the formula expressing 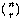 in terms
of factorials. But the technique I used in writing the
in terms
of factorials. But the technique I used in writing the combs procedure
to enumerate the actual combinations explains how Pascal's Triangle works.
The set of all combinations of n things taken r at a time can be divided
into those combinations that include the first of the n things and those
that don't. How many of the former are there? Each such combination must
be completed by adjoining to that first thing r−1 out of the remaining
n−1 available things, so there are 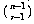 such combinations.
The second category, those not containing the first thing in the list,
requires us to choose r things out of the remaining n−1, so there are
such combinations.
The second category, those not containing the first thing in the list,
requires us to choose r things out of the remaining n−1, so there are
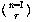 of them. So
of them. So 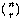 must be the sum of those two
numbers, which are indeed the ones above it in the triangle.
must be the sum of those two
numbers, which are indeed the ones above it in the triangle.
Thinking about the triangle may also help you to understand why combs
needs two stop rules; each row contains two numbers, the ones (pun)
at each end, that can't be computed as the sum of two other numbers.
Yet another approach to solving the sock problem would be the experimental method: Load a drawer with six brown and four blue socks, pull out pairs of socks a few thousand times, and see how many of the pairs match. The actual experiment would be time-consuming and rather boring, but we can simulate the experiment with a computer program. The idea is to use random numbers to represent the random choice of a sock.
to socktest
localmake "first ~
pick [brown brown brown brown brown brown blue blue blue blue]
localmake "second ~
pick (if equalp :first "brown
[[brown brown brown brown brown blue blue blue blue]]
[[brown brown brown brown brown brown blue blue blue]] )
output equalp :first :second
end
Socktest is a predicate that simulates one trial of picking
a pair of socks and outputs true if the socks match. Notice how the
available choices for the second sock depend on which color sock was chosen
first. (It's a little unaesthetic that this particular selection of six
brown and four blue socks is built into the program, with three slightly
different lists explicitly present inside socktest. It would be both
more elegant and more flexible if socktest could take a list like
[6 brown 4 blue] as input, like socks, and compute the list of
possibilities for the second sock itself. But right now I'm more interested
in showing how a simulation works than in programming style; you can make
that change yourself if you like.)
What we want to do is invoke socktest repeatedly and keep track of how
many times the output is true. That can be done with an instruction
like
print (cascade 1000 [? + if socktest [1] [0]] 0) / 10
I divide by 10 so that the result will be expressed as a percent
probability. (If I made 100 trials instead of 1000 the output from
cascade would already be a percentage.) Your results will depend on the
random number generator of your computer. I tried it three times and got
results of 50.1%, 50.8%, and 45.5%. I then did 10,000 trials at once
with a result of 48.78%. The result expected on theoretical grounds was
46 2⁄3%.
Simulation is generally much slower than either of the techniques we used earlier (enumeration of possibilities and direct computation of the number of possibilities), and it gives results that are only approximately correct. So why would anyone want to use this method? For a simple problem like this, you probably wouldn't. But some combinatorics problems are too complicated to be captured by a simple formula. For example, what is the probability of winning a game of solitaire? (To make this a sensible question, you'd have to decide on a particular set of strategy rules to determine which card to play next when there are several possibilities. The rule could be "play the higher ranking card" or "choose a card at random," for example.) In principle this question could be answered exactly, since there are only a finite number of ways a deck of cards can be arranged and we could analyze each of them. But in practice the most reasonable approach is probably to write a solitaire simulator and have it play out a few thousand randomly ordered hands.
Solitaire is a rather complicated game; even a simulator for it would be quite a large project. A more manageable one, if you'd like something to program, would be a craps simulator. Remember that the 11 possible results of rolling two dice (2 to 12) are not equally likely! You have to simulate each die separately.
This is a picture of a Simplex lock, so called because it's manufactured by Simplex Security Systems, Inc. It is a five-button mechanical (i.e., no electricity) combination lock with an unusual set of possible combinations. As an example of a challenging problem in combinatorics, I'd like you to figure out how many possible combinations there are.

What makes this lock unusual is that a combination can include more than one button pushed at the same time. For example, one possible combination is "2, then 1 and 4 at the same time, then 3." Here are the precise rules:
| 1. | Each button may be used at most once. For example, "2, then 2 and 3 at the same time" is not allowed. | |
|---|---|---|
| 2. | Each push may include any number of buttons, from one to five. For example, one legal combination is "hit all five buttons at once with your fist." (But hitting all five buttons can't be part of a larger combination because of rule 1.) |
It follows from these rules that there can be at most five distinct pushes. (Do you see why?) The rules also allow for the null combination, in which you don't have to push any buttons at all.
When working on this problem, don't forget that when two or more buttons are pushed at the same time, their order doesn't matter. That is, you shouldn't count "2 and 3 together, then 5" and "3 and 2 together, then 5" as two distinct combinations. (For this reason, the Simplex lock is entitled, at least in part, to the name "combination lock"!)
Try to figure out how many combinations there are before reading further. You can enumerate all the possibilities or you can derive a formula for the number of possibilities. You might want to start with a smaller number of buttons. (As a slight hint, when you buy one of these locks, the box it comes in says "thousands of combinations.")
I first attacked this problem by trying to enumerate all the possible
combinations, but that turns out to be quite messy. The trouble is that it
isn't obvious how to order the combinations, so it's hard to be sure
you haven't missed any. Here is how I finally decided to do it. First of
all, divide the possible combinations into six categories depending on how
many buttons (zero to five) they use. There is exactly one combination
using zero buttons, and there are five using one button each. After that it
gets tricky because there are different patterns of simultaneous
pushes within each category. For example, for combinations using two
buttons there are two patterns: the one in which they're pressed together
(x-x) and the one in which they're pressed separately (x x).
(I'm introducing a notation for patterns in which hyphens connect buttons
that are pressed together and spaces connect the separate pushes.) How many
distinct combinations are there in each of those patterns? Figure it out
before reading on.
In the x x pattern there are 5P2 "combinations" because the
order in which you push the buttons matters. In the x-x pattern there
are only 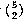 combinations because the two buttons are pushed
together;
combinations because the two buttons are pushed
together; 1-4 and 4-1 are the same combination. Altogether
there are 20+10 or 30 combinations usng two of the five buttons.
Beyond this point it gets harder to keep track of the different patterns.
Among the three-button patterns are x-x x, x x x, and
x-x-x. How many more are there? How many four-button patterns? You might,
at this point, like to see if you can finish enumerating all the
possibilities for the five-button lock.
My solution is to notice that in a three-button pattern, for example, there
are two slots between the xs, and each slot has a space or a hyphen.
If I think of those slots as binary digits, with 0 for space and 1 for
hyphen, then each pattern corresponds to a 2-bit number. There are four
such numbers, 00 to 11 (or 0 to 3 in ordinary decimal notation).
| number | pattern | |
|---|---|---|
00 01 10 11 |
x x x x x-x x-x x x-x-x |
Similarly, there are eight four-button patterns:
| number | pattern | |
|---|---|---|
000 001 010 011 100 101 110 111 |
x x x x x x x-x x x-x x x x-x-x x-x x x x-x x-x x-x-x x x-x-x-x |
And there are 16 five-button patterns, from 0000 to 1111.
How many combinations are there within each pattern? There are two
different ways to go about calculating that number. To be specific, let's
consider four-button patterns. The way I chose to do the calculation was to
start with the idea that there are 5P4 ways to choose four buttons in
order. For the x x x x pattern, this is the answer. For the other
patterns, this number (120) has to be divided by various factors to account
for the fact that the order is partially immaterial, just as in
deriving the formula for combinations from the formula for permutations we
divided by r! because the order is completely immaterial. Consider the
pattern x-x x x. In this pattern the order of the first two numbers
is immaterial, but the choice of the first two numbers as a pair matters,
and so does the order of the last two numbers. So 1-2 3 4 is the same
combination as 2-1 3 4 but different from 1-3 2 4 or
1-2 4 3. That means the number 120 is too big by a factor of 2, because
every significant choice of combination is represented twice. For this
pattern the number of different combinations is 60. Of course the same
argument applies to the patterns x x-x x and x x x-x.
What about x-x x-x? In this pattern there are two pairs of positions
within which order doesn't matter. Each combination appears four
times in the list of 120; 1-2 3-4 is the same as 1-2 4-3,
2-1 3-4, and 2-1 4-3. So there are 30 significantly different
combinations in this pattern. What about x-x-x x? In this pattern,
the order of the first three numbers is irrelevant; this means that there
are 3! or 6 appearances of each combination in the 120, so there are 20
significantly different combinations in this pattern. The general rule is
that for each group of m consecutive hyphens in the pattern you must
divide by (m+1)! to eliminate duplicates.
(My approach was to start with permutations and then divide out redundant
ones. Another approach would be to build up the pattern using combinations.
The pattern x-x x x contains three groups of numbers representing
three "pushes": a group of two and two groups of one. Since this is a
five-button lock, for the first group of two there are 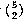 choices.
(Order doesn't matter within a group.) For the second group there are only
three buttons remaining from which we can choose, so there are
choices.
(Order doesn't matter within a group.) For the second group there are only
three buttons remaining from which we can choose, so there are 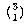 choices for that button. Finally, there are
choices for that button. Finally, there are 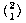 choices for the
fourth button (the third group). This makes 10×3×2 possible
combinations for this pattern, the same as the 60 we computed the other way.
For the
choices for the
fourth button (the third group). This makes 10×3×2 possible
combinations for this pattern, the same as the 60 we computed the other way.
For the x-x x-x pattern this method gives 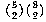 or 30 combinations.)
or 30 combinations.)
Having worked all this out, I was ready to write a computer program to count the total number of combinations. The trickiest part was deciding how to deal with the binary numbers that represent the patterns. In the end I used plain old numbers. The expression
remainder :number 2
yields the rightmost bit of a number, and then :number/2
gives all but the rightmost bit (with a little extra effort for odd numbers).
To help you read the program, here is a description of the most important
procedures:
lock 5 | outputs the total number of combinations for the 5-button lock. | |
|---|---|---|
lock1 5 4 | outputs the number of combinations that use 4 out of the 5 buttons. | |
lock2 120 5 1 | outputs the number of combinations for the 4-button pattern corresponding to the binary form of the number 5 (101 or x-x x-x). The 120 is 5P4 and the 1 is always used as the third input except in recursive calls. |
Here is the program:
to lock :buttons
output cascade :buttons [? + lock1 :buttons #] 1
end
to lock1 :total :buttons
localmake "perms perms :total :buttons
output cascade (twoto (:buttons-1)) ~
[? + lock2 :perms #-1 1] ~
0
end
to twoto :power
output cascade :power [2 * ?] 1
end
to lock2 :perms :links :factor
if equalp :links 0 [output :perms/(fact :factor)]
if equalp (remainder :links 2) 0 ~
[output lock2 :perms/(fact :factor) :links/2 1]
output lock2 :perms (:links-1)/2 :factor+1
end
One slight subtlety is that in lock the third input to
cascade is 1 rather than 0 to include the one 0-button combination
that would not otherwise be added in.
When I wrote that program, I was pleased with myself for managing to turn such a messy solution into executable form, but I wasn't satisfied with the underlying approach. I wanted something mathematically more elegant.
What made it possible for me to find the approach I wanted was the chance discovery that the number of combinations that use all five buttons (541) is half of the total number of combinations (1082). Could this possibly be a coincidence, or would that have to be true for any number of buttons? To see that it has to be true, I used an idea from another branch of mathematics, set theory. A set is any collection of things, in no particular order. One can speak of the set of all the fingers on my left hand, or the set of all the integers, or the set of all the universities in cities named Cambridge. Much of the interesting part of set theory has to do with the properties of infinite sets; for example, it turns out that the set of all the integers is the same size as the set of all the rational numbers, but both of these are smaller than the set of irrational numbers. What does it mean for one infinite set to be the same size as, or to be larger than, another? The same definition works equally well for finite sets: Two sets are the same size if they can be placed in one-to-one correspondence. This means that you must exhibit a way to pair the elements of one set with the elements of the other so that each element of one has exactly one partner in the other. (A set is larger than another if they aren't the same size, but a subset of the first is the same size as the second.)
To prove that my observation about the lock combinations has to be true
regardless of the number of buttons, I have to exhibit a one-to-one
correspondence between two sets: the set of all combinations using all
the buttons of an n-button lock and the set of all combinations using
fewer than n of the buttons. But that's easy. Starting with a
combination that uses all the buttons, just eliminate the last push (one or
more buttons pushed at the same time) to get a combination using fewer than
all the buttons. For example, for a five-button lock, the five-button
combination 2 3-4 1-5 is paired with the three-button combination
2 3-4. (We have to eliminate the last push and not merely
the last button for two reasons. First, if we always eliminated
exactly one button, we'd always get a four-button combination, and we want
to pair five-button combinations with all the fewer-than-five ones.
Second, which is the "last" button if the last push involves more than
one? Remember, 2 3-4 1-5 is the same combination as
2 3-4 5-1. But writing this combination in two different forms
seems to pair it with two different smaller ones. The rules of one-to-one
correspondence say that each element of a set must have exactly one partner
in the other set.)
To show that the correspondence works in both directions, start with a
combination that doesn't use all the buttons; its partner is formed by
adding one push at the end that contains all the missing buttons.
For example, if we start with 1 2-5 then its partner is
1 2-5 3-4.
I've just proved that the number of all-n combinations must be equal to the number of fewer-than-n combinations. So it's not a coincidence that 541 is half of 1082. In order to be able to talk about these numbers more succinctly, I want to define
We've just proved that it's also true that
Now, what does "fewer than n buttons" mean? Well, there are combinations using no buttons, one button, two buttons, and so on up to n−1 buttons. Let's define
So we can formalize the phrase "fewer than n" by saying
Instead of using those dots in the middle, mathematicians have another notation for a sum of several terms like this.
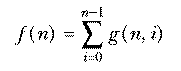
If you haven't seen this notation before, the Σ (sigma)
symbol is the Greek letter S, and is used to represent a Sum.
It works a little like the for iteration tool; the variable below the
Σ (in this case, i) takes on values from the lower limit (0) to the
upper limit (n−1), and for each of those values the expression following the
Σ is added into the sum. The Logo equivalent would be
for [i 0 [:n-1]] [make "sum :sum + (g :n :i)]
The Σ-expression is pronounced "the sum from i equals zero to n minus one of g of n comma i."
So far, what I've done is like what I did before: dividing the set of all
possible combinations into subsets based on the number of buttons used in
each combination. This is like the definition of lock in terms of
lock1. The next step is to see if we can find a formula for g(n,i).
How many 3-button combinations, for example, can we make using a 5-button
lock? (That's g(5,3).) There are many different ways in which I might
try to derive a formula, but I think it will be helpful at this point to
step back and consider my overall goal. I started this line of reasoning
because I'm trying to express the solution for the five-button lock in terms
of easier solutions for smaller numbers of buttons. That is, I'm looking
for an inductive definition of f(n) in terms of values of f for smaller
arguments. I'd like to end up with a formula like
but I don't yet know exactly what form it will take. So far I've written a formula for f(n) in terms of g(n,i) for values of i less than n. It would be great, therefore, if I could express g(n,i) in terms of f(i); that would give me exactly what I want.
To put that last sentence into words, it would be great if I could express
the number of i-button combinations of an n-button lock in terms of the
number of i-button combinations of an i-button lock. For example, can I
express the number of combinations using 3 out of 5 buttons in terms of the
number of combinations of 3 out of 3 buttons? Yes, I can. The latter is
the number of rearrangements of three buttons once we've selected the three
buttons. If we start with five buttons, there are 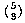 possible
sets of three buttons to choose. For each of those
possible
sets of three buttons to choose. For each of those 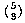 sets of
three buttons, there are f(3) ways to arrange those three buttons in a
combination.
sets of
three buttons, there are f(3) ways to arrange those three buttons in a
combination.
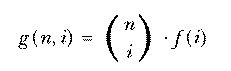
It may not be obvious why this is so. Suppose you list all the 3-button combinations of a 3-button lock. There are 13 of them, consisting of the numbers from 1 to 3 in various orders and with various groups connected by hyphens. Those 13 combinations are also some of the 3-button combinations of a 5-button lock, namely, the ones in which the particular three buttons we chose are 1, 2, and 3. If instead we choose a different set of three (out of five) buttons, that gives rise to a different set of 13 combinations. For example, if we choose the buttons 2, 3, and 4, we can take the original 13 combinations and change all the 1s to 2s, all the 2s to 3s, and all the 3s to 4s:
buttons: 1,2,3 2,3,4 1,4,5
1 2 3 2 3 4 1 4 5
1 3 2 2 4 3 1 5 4
2 1 3 3 2 4 4 1 5
2 3 1 3 4 2 4 5 1
3 1 2 4 2 3 5 1 4
3 2 1 4 3 2 5 4 1
1 2-3 2 3-4 1 4-5
2 1-3 3 2-4 4 1-5
3 1-2 4 2-3 5 1-4
1-2 3 2-3 4 1-4 5
1-3 2 2-4 3 1-5 4
2-3 1 3-4 2 4-5 1
1-2-3 2-3-4 1-4-5
This table has a column for each of three possible combinations of
five numbers three at a time. The table could be extended to have a column
for every such combination of numbers, and then it would contain all
the lock combinations using three out of five buttons. The total number of
entries in the extended table is therefore g(5,3); the table has f(3)
rows and 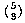 columns. So
columns. So
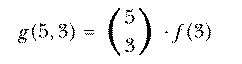
which is a particular case of the general formula above.
We now have a formula for f(n) in terms of all the g(n,i) and a formula for g(n,i) in terms of f(i). Combining these we have
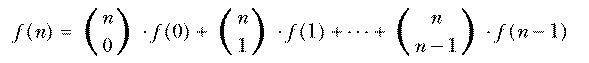
or
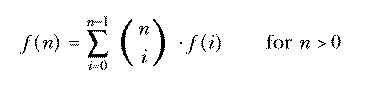
Like any inductive definition, this one needs a special rule for the smallest case, from which all the others are computed:
The total number of combinations for an n-button lock is 2×f(n). I find this much more elegant than my original solution. (So why didn't I just show you this one to begin with? Because I never would have figured this one out had I not first done the enumeration of cases. I want you to see how a combinatorics problem is solved, not just what the beautiful solution looks like.) This formula can also be turned into a computer program:
to simplex :buttons output 2 * f :buttons end to f :n if equalp :n 0 [output 1] output cascade :n [? + ((choose :n (#-1)) * f (#-1))] 0 end to choose :n :r output (perms :n :r)/(fact :r) end
This program is faster as well as simpler than the other; on my
home computer, lock 5 takes about 4 seconds, simplex 5 about 2 seconds.
The simplex function has no exact closed form equivalent, but it turns
out that there is (amazingly!) a closed form definition that, when rounded
to the nearest integer, gives the desired value:
to simp :n output round (fact :n)/(power (ln 2) (:n+1)) end
The ln function, a Logo primitive, computes the "natural
logarithm" of its input; ln 2 has the approximate value 0.69314718056.
The power function of two inputs takes
the first input to the power of the second input. Fact is the
factorial function as defined earlier in this chapter.
Another related programming problem is to list the actual combinations,
rather than merely count them. Probably the simplest way to do that is
to use an approach similar to the one I used in the combs procedure
that lists combinations of members of a list: First use recursion to
find the lock combinations using only the butfirst of the available
buttons, then find the ways in which the first button can be added
to each of them.
Earlier, in talking about Pascal's Triangle, I showed how binomial coefficients are related to combinations and asked you to think about trinomial coefficients. What, for example, is the coefficient of ab2c in the expansion of (a+b+c)4?
The expansion is a sum of products; each of those products contains four
variables (aaaa, aaab, etc.). The ones that contribute to the ab2c
term are the ones with one A, two Bs, and one c; these include
abbc, bcab, cabb, and so on. Out of the four slots for variables in
one of those products, how many ways can we choose a slot for one A? The
answer is 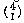 . Having chosen one, we are left with three slots
and we want to choose two of them for Bs. There are
. Having chosen one, we are left with three slots
and we want to choose two of them for Bs. There are 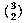 ways to
do that. Then we have one slot left, just enough for the one c, which
makes a trivial contribution of
ways to
do that. Then we have one slot left, just enough for the one c, which
makes a trivial contribution of 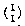 to the overall number of
possibilities. The total is
to the overall number of
possibilities. The total is 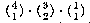 or 4×3×1 or 12, and that is the coefficient of
ab2c. Similarly, the coefficient of ac3 is
or 4×3×1 or 12, and that is the coefficient of
ab2c. Similarly, the coefficient of ac3 is 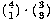 or 4.
or 4.
The same sort of argument can be used for even more complicated cases. In the expansion of (a+b+c+d+e)14 what is the coefficient of a2b3cd5e3? It's
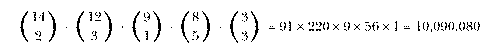
Here is a harder question: How many terms are there in, say, (a+b+c+d)7? It's easy to see that there are 47 products of four variables, but after the ones that are equal to each other have been combined into terms, how many distinct terms are there?
Like the Simplex lock problem, this one can probably be solved most easily
by reducing the problem to a smaller subproblem--in other words, by an
inductive definition. This problem also has something in common with the
earlier problem of listing all the combinations of a given size from a
given list, as we did in the combs procedure. Try to solve the
problem before reading further. (It's hard to say how another person will
find a problem, but I think this one is easier than the Simplex one.)
In order to be able to express the original problem in terms of a smaller version, we have to generalize it. I posed a specific problem, about the seventh power of the sum of four variables. I'd like to be able to give the answer to that problem the name t(4,7) and try to find a way to express that in terms of, let's say, t(4,6). So I'm going to define the function t as
(If this were a "straight" math book I'd cheerfully recycle the name f
for the function, even though we had a different f in the last section,
but I'm anticipating wanting to write a Logo program for this problem and I
can't have two procedures named f in the same workspace.)
In writing combs I used the trick of dividing all possible
combinations into two groups: those including the first member of the list
and those not including that member. A similar trick will be useful here;
we can divide all the terms in an expansion into two groups. One group will
contain those terms that include the first variable (a1) and the other
will contain the rest. For example, in the original problem, a2b3d2 is
a term in the first group, while c7 is a term in the second group.
A term in the first group can be divided by a1; the result must be a term in the expansion of (a1+a2+ ··· +an)k−1. How many such terms are there? There are t(n,k−1) of them. So that's how many terms there are in the first group.
A term in the second group is a product of k variables not including a1. That means that such a term is also part of the expansion of (a2+ ··· +an)k. How many such terms are there? There are t(n−1,k) of them. Notice the difference between the two groups. In the first case, we associate a term with a similar term in the expansion of an expression involving a smaller power of the same number of variables. In the second case, we associate a term with an equal term in the expansion of an expression involving fewer variables taken to the same power.
Combining these two results, we see that
Since this is a function of two variables, it needs two "stop rules," just
like the function 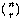 . Picking these limiting cases seems much
simpler than inventing the induction rule, but even so, it may repay some
attention. For the rule
. Picking these limiting cases seems much
simpler than inventing the induction rule, but even so, it may repay some
attention. For the rule
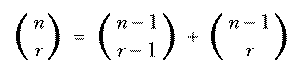
we ended up considering the limiting cases r=0 and r=n. I didn't say anything about it at the time because I didn't want to get distracted, but it's not obvious why there is the asymmetry between the two variables in those limiting cases. That is, why didn't I pick r=0 and n=0 as the limiting cases? That would be more like what you're accustomed to in recursive Logo procedures, where stop rules almost always involve a comparison of something with zero or with the empty list.
The funny limiting cases for 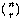 (and the corresponding funny stop
rules in
(and the corresponding funny stop
rules in combs) are related to the fact that this function is
meaningful only when n≥r. The two arguments can't be chosen
independently. If we didn't have the r=n limiting case, the inductive
formula would have us compute
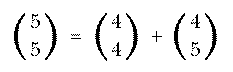
If we define 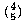 as zero, this equation does turn out to be true,
but it isn't a very sensible way to compute
as zero, this equation does turn out to be true,
but it isn't a very sensible way to compute 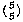 .
.
In the case of the function t, the two arguments are independent. Both t(4,7) and t(7,4) are sensible things to ask for. Therefore, we should use the more obvious limiting cases n=0 and k=0. The trouble is that it's not obvious what the value of t(0,k) or t(n,0) should be. The first of these, t(0,k), represents the number of terms in the expansion of ()k--nothing to the kth power! That seems meaningless. On the other hand, t(n,0) represents the number of terms in (∑ ai)0, which is 1. Anything to the zeroth power is 1. Does "1" count as a term? It doesn't have any variables in it.
One solution would be to take as limiting cases n=1 and k=1. It's much easier to see what those values should be. (a1)k has one term, so t(1,k)=1. And (a1+ ··· +an)1 has n terms, so t(n,1)=n. We could, then, define the function t as
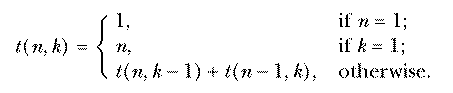
But it is possible to figure out appropriate values for zero arguments by working backwards from the cases we already understand. For example, we know that t(2,1) must equal 2. But
It follows that t(2,0) must be 1. So it's reasonable to guess that t(n,0)=1 will work in general. Similarly, we know that t(1,2)=1, but
Therefore t(0,2) must be 0. We can define t as
What is t(0,0)? The definition above contradicts itself about this. The answer should be 0 because n=0 but also 1 because k=0. This reminds me of the similar problem about powers of integers. What is 00? In general 0x=0 but x0=1, for nonzero x. There is really no "right" answer, but mathematicians have adopted the convention that 00=1. To make our definition of t truly correct I have to choose a convention for t(0,0) and modify the definition to reflect it:
It's straightforward to translate this mathematical function definition into a Logo procedure:
to t :n :k if equalp :k 0 [output 1] if equalp :n 0 [output 0] output (t :n :k-1)+(t :n-1 :k) end
Using this function we can compute t 4 7 and find that the
answer to the original problem is 120.
(Can you write a program to display the actual expansion? That is, it should print something like
(A+B+C+D)^7 = 1 A^7 + 7 A^6 B + 21 A^5 B^2 + ...
There are two parts to this problem. One is to figure out the
combinations of variables in the 120 terms, which can be done with a
procedure like combs, and the other is to figure out the coefficients,
which I discussed at the beginning of this section.)
I was introduced to this problem as a student teacher in a high school probability class. The teacher gave "how many terms are there in the expansion of (a+b+c+d)7" as a quiz problem, and nobody answered it. In the ensuing class discussion, it turned out that she meant the students to answer the much easier question of how many products of seven variables there are. As I noted earlier, the answer to that question is just 47. But all the students interpreted the question as meaning the harder one we've been exploring here. I took the problem home that evening and reached the point we've reached in this chapter. I didn't think I could get a better answer than that until my housemate taught me about generating functions. It turns out that there is a closed form definition for this function:
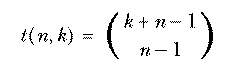
This definition is faster to compute as well as more beautiful.
Once armed with the formula, it wasn't hard to invent a way to demonstrate that it must be correct without going through the inductive definition and the use of calculus. The trick is that we must be choosing n−1 somethings out of a possible k+n−1 for each term. What does a term look like? Ignoring the constant coefficient, it is the product of k (seven, in the specific problem given) variables, some of which may be equal. Furthermore, when the terms are written in the usual way, the variables come in alphabetical order. A term like a2b4d represents aabbbbd; there won't be a different term with the same letters in another order. In general, the k variables will be some number (zero or more) of a1s, then some number of a2s, and so on.
Now comes the trick. Suppose we write the string of variables with a "wall" for each change to the next letter. So instead of aabbbbd I want to write aa|bbbb||d. (There are two walls before the final d to reflect the fact that we skipped over c.) In this notation there are always exactly n−1 walls. (That's why I chose to put the walls in; remember, we're looking for n−1 of something.) The term includes k variables and n−1 walls, for a total of k+n−1 symbols.
Once the walls are there, it really is no longer necessary to preserve the individual variable letters. The sample term we've been using could just as well be written xx|xxxx||x. What comes before the first wall is the first variable letter, and so on. So ||xxx|xxxx represents c3d4. But now we're finished. We have found a way to represent each possible term as a string of k copies of the letter x interspersed with n−1 walls. How many such arrangements are there? How many ways are there to choose n−1 positions for walls in a string of k+n−1 symbols?
Earlier, in talking about the difference between closed form and inductive definitions, I suggested that the an inductive definition might be much easier to discover even if a closed form definition also exists. This is a clear example. If I'd given the demonstration just above, with xs and walls, without first showing you the more roundabout way I really discovered the definition, you'd rightly complain about rabbits out of hats.
| (back to Table of Contents) | BACK chapter thread NEXT |
;;; Logic problem inference system
;; Establish categories
to category :category.name :members
print (list "category :category.name :members)
if not namep "categories [make "categories []]
make "categories lput :category.name :categories
make :category.name :members
foreach :members [pprop ? "category :category.name]
end
;; Verify and falsify matches
to verify :a :b
settruth :a :b "true
end
to falsify :a :b
settruth :a :b "false
end
to settruth :a :b :truth.value
if equalp (gprop :a "category) (gprop :b "category) [stop]
localmake "oldvalue get :a :b
if equalp :oldvalue :truth.value [stop]
if equalp :oldvalue (not :truth.value) ~
[(throw "error (sentence [inconsistency in settruth]
:a :b :truth.value))]
print (list :a :b "-> :truth.value)
store :a :b :truth.value
settruth1 :a :b :truth.value
settruth1 :b :a :truth.value
if not emptyp :oldvalue ~
[foreach (filter [equalp first ? :truth.value] :oldvalue)
[apply "settruth butfirst ?]]
end
to settruth1 :a :b :truth.value
apply (word "find not :truth.value) (list :a :b)
foreach (gprop :a "true) [settruth ? :b :truth.value]
if :truth.value [foreach (gprop :a "false) [falsify ? :b]
pprop :a (gprop :b "category) :b]
pprop :a :truth.value (fput :b gprop :a :truth.value)
end
to findfalse :a :b
foreach (filter [not equalp get ? :b "true] peers :a) ~
[falsify ? :b]
end
to findtrue :a :b
if equalp (count peers :a) (1+falses :a :b) ~
[verify (find [not equalp get ? :b "false] peers :a)
:b]
end
to falses :a :b
output count filter [equalp "false get ? :b] peers :a
end
to peers :a
output thing gprop :a "category
end
;; Common types of clues
to differ :list
print (list "differ :list)
foreach :list [differ1 ? ?rest]
end
to differ1 :a :them
foreach :them [falsify :a ?]
end
to justbefore :this :that :lineup
falsify :this :that
falsify :this last :lineup
falsify :that first :lineup
justbefore1 :this :that :lineup
end
to justbefore1 :this :that :slotlist
if emptyp butfirst :slotlist [stop]
equiv :this (first :slotlist) :that (first butfirst :slotlist)
justbefore1 :this :that (butfirst :slotlist)
end
;; Remember conditional linkages
to implies :who1 :what1 :truth1 :who2 :what2 :truth2
implies1 :who1 :what1 :truth1 :who2 :what2 :truth2
implies1 :who2 :what2 (not :truth2) :who1 :what1 (not :truth1)
end
to implies1 :who1 :what1 :truth1 :who2 :what2 :truth2
localmake "old1 get :who1 :what1
if equalp :old1 :truth1 [settruth :who2 :what2 :truth2 stop]
if equalp :old1 (not :truth1) [stop]
if memberp (list :truth1 :who2 :what2 (not :truth2)) :old1 ~
[settruth :who1 :what1 (not :truth1) stop]
if memberp (list :truth1 :what2 :who2 (not :truth2)) :old1 ~
[settruth :who1 :what1 (not :truth1) stop]
store :who1 :what1 ~
fput (list :truth1 :who2 :what2 :truth2) :old1
end
to equiv :who1 :what1 :who2 :what2
implies :who1 :what1 "true :who2 :what2 "true
implies :who2 :what2 "true :who1 :what1 "true
end
to xor :who1 :what1 :who2 :what2
implies :who1 :what1 "true :who2 :what2 "false
implies :who1 :what1 "false :who2 :what2 "true
end
;; Interface to property list mechanism
to get :a :b
output gprop :a :b
end
to store :a :b :val
pprop :a :b :val
pprop :b :a :val
end
;; Print the solution
to solution
foreach thing first :categories [solve1 ? butfirst :categories]
end
to solve1 :who :order
type :who
foreach :order [type "| | type gprop :who ?]
print []
end
;; Get rid of old problem data
to cleanup
if not namep "categories [stop]
ern :categories
ern "categories
erpls
end
;; Anita Harnadek's problem
to cub.reporter
cleanup
category "first [Jane Larry Opal Perry]
category "last [Irving King Mendle Nathan]
category "age [32 38 45 55]
category "job [drafter pilot sergeant driver]
differ [Jane King Larry Nathan]
says "Jane "Irving 45
says "King "Perry "driver
says "Larry "sergeant 45
says "Nathan "drafter 38
differ [Mendle Jane Opal Nathan]
says "Mendle "pilot "Larry
says "Jane "pilot 45
says "Opal 55 "driver
says "Nathan 38 "driver
print []
solution
end
to says :who :what1 :what2
print (list "says :who :what1 :what2)
xor :who :what1 :who :what2
end
;; Diane Baldwin's problem
to foote.family
cleanup
category "when [1st 2nd 3rd 4th 5th]
category "name [Felix Fred Frank Francine Flo]
category "street [Field Flag Fig Fork Frond]
category "item [food film flashlight fan fiddle]
category "position [1 2 3 4 5]
print [Clue 1]
justbefore "Flag "2nd :position
justbefore "2nd "Fred :position
print [Clue 2]
male [film Fig 5th]
print [Clue 3]
justbefore "flashlight "Fork :position
justbefore "Fork "1st :position
female [1st]
print [Clue 4]
falsify "5th "Frond
falsify "5th "fan
print [Clue 5]
justbefore "Francine "Frank :position
justbefore "Francine "Frank :when
print [Clue 6]
female [3rd Flag]
print [Clue 7]
justbefore "fiddle "Frond :when
justbefore "Flo "fiddle :when
print []
solution
end
to male :stuff
differ sentence :stuff [Francine Flo]
end
to female :stuff
differ sentence :stuff [Felix Fred Frank]
end
;;; Combinatorics toolkit
to combs :list :howmany
if equalp :howmany 0 [output [[]]]
if equalp :howmany count :list [output (list :list)]
output sentence (map [fput first :list ?]
combs (butfirst :list) (:howmany-1)) ~
(combs (butfirst :list) :howmany)
end
to fact :n
output cascade :n [# * ?] 1
end
to perms :n :r
if equalp :r 0 [output 1]
output :n * perms :n-1 :r-1
end
to choose :n :r
output (perms :n :r)/(fact :r)
end
;; The socks problem
to socks :list
localmake "total combs (expand :list) 2
localmake "matching filter [equalp first ? last ?] :total
print (sentence [there are] count :total [possible pairs of socks.])
print (sentence [of these,] count :matching [are matching pairs.])
print sentence [probability of match =] ~
word (100 * (count :matching)/(count :total)) "%
end
to expand :list
if emptyp :list [output []]
if numberp first :list ~
[output cascade (first :list)
[fput first butfirst :list ?]
(expand butfirst butfirst :list)]
output fput first :list expand butfirst :list
end
to socktest
localmake "first pick [brown brown brown brown brown brown
blue blue blue blue]
localmake "second ~
pick (ifelse equalp :first "brown ~
[[brown brown brown brown brown
blue blue blue blue]] ~
[[brown brown brown brown brown brown
blue blue blue]])
output equalp :first :second
end
;; The Simplex lock problem
to lock :buttons
output cascade :buttons [? + lock1 :buttons #] 1
end
to lock1 :total :buttons
local "perms
make "perms perms :total :buttons
output cascade (twoto (:buttons-1)) [? + lock2 :perms #-1 1] 0
end
to lock2 :perms :links :factor
if equalp :links 0 [output :perms/(fact :factor)]
if equalp (remainder :links 2) 0 ~
[output lock2 :perms/(fact :factor) :links/2 1]
output lock2 :perms (:links-1)/2 :factor+1
end
to twoto :power
output cascade :power [2 * ?] 1
end
to simplex :buttons
output 2 * f :buttons
end
to f :n
if equalp :n 0 [output 1]
output cascade :n [? + ((choose :n (#-1)) * f (#-1))] 0
end
to simp :n
output round (fact :n)/(power (ln 2) (:n+1))
end
;; The multinomial expansion problem
to t :n :k
if equalp :k 0 [output 1]
if equalp :n 0 [output 0]
output (t :n :k-1)+(t :n-1 :k)
end
Brian Harvey,
bh@cs.berkeley.edu