| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |
|
|
Program file for this chapter: algs
What's wrong with this procedure?
to process.sentence :sent output fput (process.word first :sent) (process.sentence bf :sent) end
If you said "It's a recursive procedure without a stop rule," you've solved a simple problem in analysis of algorithms. This branch of computer science is concerned with the correctness and the efficiency of programs.
The field is called analysis of algorithms rather than analysis of programs because the emphasis is on the meaning of a program (how you might express the program in English) and not on the details of its expression in a particular language. For example, the error in the procedure
to process.sentence :sent if emptyp :sent [output []] output fput (process.word first :sent) (process.snetence bf :sent) end
is just as fatal as the error in the first example, but there isn't much of theoretical interest to say about a misspelled procedure name. On the other hand, another branch of computer science, program verification, is concerned with developing techniques to ensure that a computer program really does correctly express the algorithm it is meant to express.
The examples I've given so far are atypical, it's worth noting, in that you
were able to see the errors in the procedures without having any real idea
of what they do! Without seeing process.word you can tell that this
program is doing something or other to each word of a sentence, but you
don't know whether the words are being translated to another language,
converted from upper case to lower case letters, translated into a string of
phoneme codes to be sent to a speech synthesizer, or what. (Even what I just
said about doing something to the words of a sentence is an inference based
on the names of procedures and variables, which might not really reflect the
results of the program.) More interesting problems in analysis of
algorithms have to do with the specific properties of particular algorithms.
In this chapter I discuss algorithms along with data structures, the different ways in which information can be represented in a computer program, because these two aspects of a program interact strongly. That is, the choices you make as a programmer about data representation have a profound effect on the algorithms you can use to solve your problem. Similarly, once you have chosen an algorithm, that choice determines the particular kinds of information your program will need to do its work. Algorithms and data structures are the central concerns of software engineering, the overall name for the study of how to turn a problem statement into a working program in a way that uses both the computer and the programming staff effectively.
When you're trying to make a computer program run as fast as possible, the most obvious place to start is with the details of the instructions in the program. But that's generally not the most effective approach. Rethinking the big picture can give much more dramatic improvements. To show you what I mean, I'll give some examples of both. Later I'll talk about order of growth, a more formal way to understand this same idea.
Consider the following procedure that implements the quadratic formula
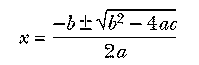
This formula gives the two values of x that solve the equation
to quadratic :a :b :c localmake "x1 (-:b + sqrt (:b*:b - 4*:a*:c))/2*:a localmake "x2 (-:b - sqrt (:b*:b - 4*:a*:c))/2*:a print (sentence [The solutions are] :x1 "and :x2) end
Before we talk about the efficiency of this program, is it correct?
This is not a simple yes-or-no question. The procedure gives the correct
results for those quadratic equations that have two real solutions. For
example, the equation 2x2+5x-3 = 0 has the solutions x = −3 and ½; the instruction quadratic 2 5 -3 will print those solutions.
Some quadratic equations, like x2-8x+16 = 0, have only one solution; for
these equations, quadratic prints the same solution twice, which is
not exactly incorrect but still a little embarrassing. Other equations,
like x2+1 = 0, have solutions that are complex numbers. Depending on our
purposes, we might want quadratic to print the solutions i and −i
for this equation, or we might want it to print "This equation has no real
solutions." But since most versions of Logo do not provide complex
arithmetic, what will really happen is that we'll get the error message
sqrt doesn't like -1 as input.
If quadratic is used as part of a larger project, getting
the Logo error message means that the program dies altogether in this case
without a chance to recover. If we have several equations to
solve, it would be better if the program could continue to the remaining
equations even if no solution is found for one of them. A program that
operates correctly for the kinds of inputs that the programmer had in mind,
but blows up when given unanticipated inputs, is said not to be
robust; a robust program should do something appropriate even if there
are errors in its input data.
But my real reason for displaying this example is to discuss its efficiency. It computes the expression
sqrt (:b*:b - 4*:a*:c)
twice. Multiplication is slower than addition on most computers; this expression involves three multiplications as well as the even slower square root extraction. The program would be faster if it were written this way:
to quadratic :a :b :c localmake "sqrt sqrt (:b*:b - 4*:a*:c) localmake "x1 (-:b + :sqrt)/2*:a localmake "x2 (-:b - :sqrt)/2*:a print (sentence [The solutions are] :x1 "and :x2) end
This kind of change to a program is called
common subexpression elimination. It's a
pretty easy way to speed up a program;
so easy, in fact, that some "optimizing compilers" for large computers do
it automatically. In other words, an optimizing compiler for Logo would
treat the first version of quadratic as if it were written like the
second version. (As far as I know, nobody has actually written such a
compiler for Logo.)
Common subexpression elimination is an example of local optimization.
This means that we improved the program by paying attention to one small
piece of it at a time. (A less elegant name for local optimization is "code
bumming.") Is it worth the effort? It depends how many times this procedure
will be run. When I say that multiplication is slow, I mean that it takes
a few millionths of a second. If you are writing a quadratic
procedure to do the dozen problems in your high school algebra homework, the
extra time you spend thinking up the second version and typing it into the
editor probably outweighs the saving of time in running the procedure. But
if you are trying to predict the weather and need to solve tens of thousands
of equations, the saving may be significant.
If you want to write locally optimized
Logo programs, it's important to know that first, butfirst, and
fput take a constant amount of time regardless of the length of the
input list, whereas last, butlast, and lput take an amount
of time proportional to the length of the list. If you add n items to a
list, one by one, using fput, the length of time required is n times
the constant amount of time for each item. But if you add the same n
items using lput, if the first item takes t microseconds, the last
takes nt. On the average, each lput takes something like nt/2
microseconds, so the total time is n2t/2. The gain in efficiency from
using fput instead of lput isn't significant if your list has
only a few items, but the gain gets more and more significant as the size of
the list increases. Suppose you want to create a list of the numbers from 1
to 1000. One straightforward way would be
print cascade 1000 [lput # ?] []
On my home computer this instruction takes about 26
seconds.* If you
just use fput in place of lput the list will come out in the
wrong order, but it's possible to reverse the order of that list to get the
same result as the first version:
*The actual time depends not only on what model of computer you have but also on how much memory and what else is in it.
print reverse cascade 1000 [fput # ?] []
You might think this would be slower, because it has the extra
reverse step. But in fact this instruction took about 12 seconds.
(It's important that the reverse tool in the Berkeley Logo
library uses first
and fput to do its work. If we used the more obvious
to reverse :list if emptyp :list [output []] output lput first :list reverse bf :list end
then the elimination of lput in the cascade template
would be offset by the lput in the reversal.)
At the other extreme, the broadest possible global optimization of a
program is to think of an entirely new algorithm based on a different way of
thinking about the original problem. As an example, in Chapter 2 there are
three different programs to solve the Simplex lock problem. The first
program, lock, works by enumerating explicitly all the different
patterns of possible combinations. That algorithm is not fundamentally
recursive; although my Logo implementation includes recursive subprocedures,
the number of combinations for a five-button lock is not determined on the
basis of the number for a four-button lock. (The program does compute the
number of combinations that use four out of the five available buttons, but
that isn't the same thing.) The second program, simplex, is based on
a mathematical argument relating the number of combinations to a fairly
simple recursive function--that is, a mathematical function with an
inductive definition. Because the function is computationally simple, the
intellectual energy I invested in doing the mathematics paid off with a
significantly faster program. The third version, simp, uses a closed
form formula that solves the problem in no time!
To illustrate more sharply the differences among these three programs, I tried each
of them on a ten-button version of the Simplex lock. To compute
lock 10 took 260 seconds on my computer; simplex 10 took 80 seconds; and
simp 10 took less than half a second. For this size lock, understanding the
mathematical idea of a recursive function sped up the program by a factor of
three, and using the mathematical technique called generating functions
achieved an additional speedup by a factor of almost 200! What's important
to understand about this example is that it wasn't better programming
skill that made the difference, but greater knowledge of mathematics.
(In the next section, though, you'll learn a programming trick that can
sometimes achieve similar speedups.)
Many "trick" math problems involve a similar shift in thinking about the fundamental algorithm to be used. For example, in Chapter 2 we computed the probability of picking a matching pair of socks out of a drawer containing six brown and four blue socks this way:
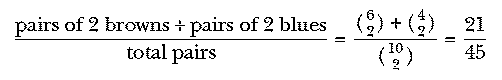
Suppose we ask this question: Out of the same drawer of six browns and two blues, we pick three socks at random; what is the probability that at least two of the socks match?
The number of triples of socks in which at least two are brown is the number
in which all three are brown, 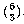 , plus the number in which two are
brown and one is blue,
, plus the number in which two are
brown and one is blue, 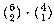 . The number in which
at least two are blue is, similarly,
. The number in which
at least two are blue is, similarly, 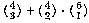 . The total number of triples is of course
. The total number of triples is of course 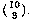 .
So the probability of a matching pair within the chosen triple is
.
So the probability of a matching pair within the chosen triple is
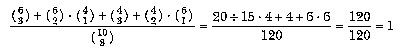
which is 100% probability.
We could modify the socks procedure to get the same result by listing
all the possible triples and then filtering all the ones containing a
matching pair, using a filter like
to haspair :triple
output or (memberp first :triple butfirst :triple) ~
(equalp (item 2 :triple) last :triple)
end
But the problem becomes entirely trivial if you notice that there are only two possible colors, so obviously there is no way that three randomly chosen socks can have three distinct colors! Of course there has to be a matching pair within any possible triple. A problem like this, that invites a messy arithmetic solution but is obvious if properly understood, is the mathematician's idea of a joke. (Did you get it?)
Some efficiency tricks are applicable to a number of different problems and become part of the "toolkit" of any professional programmer. One example is relevant to many inductively defined functions; the trick is to have the program remember the result of each invocation of the function. For example, in Chapter 2 we defined the number of terms in a multinomial expansion to be
to t :n :k if equalp :k 0 [output 1] if equalp :n 0 [output 0] output (t :n :k-1)+(t :n-1 :k) end
What happens when we compute t 4 7?
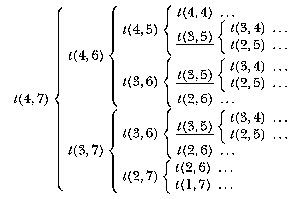
Many calculations are performed repeatedly. In the chart above I've underlined three places where t(3,5) is computed. Each of those in turn involves repeated computation of t(3,4) and so on. This computation took me about 18 seconds.
Here is a version of t that uses property lists to remember all the
values it's already computed. This version will calculate t(3,5) only the
first time it's needed; a second request for t(3,5) will instantly output
the remembered value.
to t :n :k localmake "result gprop :n :k if not emptyp :result [output :result] make "result realt :n :k pprop :n :k :result output :result end to realt :n :k if equalp :k 0 [output 1] if equalp :n 0 [output 0] output (t :n :k-1)+(t :n-1 :k) end
Computing t 4 7 isn't really a big enough problem to
show off how much faster this version is; even the original program takes
only 2 ½ seconds on my home computer. But the amount of time
needed grows quickly as you try larger inputs. Using the original procedure
from Chapter 2, my computer took just under five minutes to
compute t 8 10; the program shown here took less than two
seconds. This program computed t 12 12 in about three seconds;
I estimate that the original procedure would take five hours to
solve that problem! (As you can imagine, I didn't try it.)
The memoized version of t has the same structure as the original.
That is, in order to compute t 4 7, the program must first carry out
the two subtasks t 4 6 and t 3 7. The only difference between
the original version and the memoized version is that in the latter,
whenever a second invocation is made with inputs that have already been
seen, the result is output immediately without repeating that subtask. Any
recursive function can be memoized in the same way.*
*I've used property lists of numbers to hold the remembered values of thetfunction. If I wanted to use the same technique for some other function in the same workspace, I'd have to find a way to keep the values for the two functions from getting in each other's way. For example, if t(4,7)=120 and some other function h(4,7)=83, then I might store the value[t 120 h 83]on the appropriate property list.
Sometimes, though, the same general idea--remembering the results of past computations--can be used more effectively by changing the program structure so that just the right subproblems are solved as they're needed to work toward the overall solution. Rearranging the program structure isn't called memoization, but we're still using the same idea. For example, the Simplex lock function
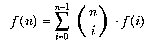
from Chapter 2
is a combination (sorry about the pun) of values of two functions. It isn't
exactly helpful to remember every possible value of 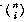 because
each value is used only once. But the calculation of f(n) uses the entire
nth row of Pascal's Triangle, and it's easy to compute that if we remember
the row above it. The values of f(i) are used repeatedly, so it makes
sense to keep a list of them. So my plan is to have two lists,
the first of which is a list of values of f(i) and the second a row of
Pascal's Triangle:
because
each value is used only once. But the calculation of f(n) uses the entire
nth row of Pascal's Triangle, and it's easy to compute that if we remember
the row above it. The values of f(i) are used repeatedly, so it makes
sense to keep a list of them. So my plan is to have two lists,
the first of which is a list of values of f(i) and the second a row of
Pascal's Triangle:
round ?1 ?2 0 [1] [1 1] 1 [1 1] [1 2 1] 2 [3 1 1] [1 3 3 1] 3 [13 3 1 1] [1 4 6 4 1] 4 [75 13 3 1 1] [1 5 10 10 5 1] 5 [541 75 13 3 1 1] [1 6 15 20 15 6 1]
The solution to the problem is twice the first member of the last
value of ?1.
Instead of starting with a request for f(5) and carrying out subtasks as needed, the new program will begin with f(0) and will work its way up to larger input values until the desired result is found. This technique is called dynamic programming:
to simplex :buttons
output 2 * first (cascade :buttons
[fput (sumprods bf ?2 ?1) ?1] [1]
[fput 1 nextrow ?2] [1 1])
end
to sumprods :a :b
output reduce "sum (map "product :a :b)
end
to nextrow :combs
if emptyp butfirst :combs [output :combs]
output fput (sum first :combs first butfirst :combs) ~
nextrow butfirst :combs
end
I tried both versions of simplex for a 12-button lock.
The version in Chapter 2 took about 5 ½ minutes to get the
answer (which is that there are about 56 billion combinations); this
version took about one second, comparable to the closed form simp
procedure.
If you just read this program with no prior idea of what algorithm it's using, it must be hard to see how it reflects the original problem. But if you think of it as a quasi-memoization of the earlier version it should make sense to you.
Every textbook on algorithms uses sorting as one of its main examples. There are several reasons for this. First of all, sorting is one of the most useful things to do with a computer, in a wide variety of settings. There are many different known sorting algorithms, ranging from obvious to subtle. These algorithms have been analyzed with great care, so a lot is known about their behavior. (What does that mean? It means we can answer questions like "How long does this algorithm take, on the average?" "How long does it take, at worst?" "If the things we're sorting are mostly in order to begin with, does that make it faster?") And all this effort pays off, in that the cleverest algorithms really are much faster than the more obvious ones.
The problem we want to solve is to take a list in unknown order and rearrange it to get a new list of the same members in some standard order. This might be alphabetical order if the members of the list are words, or size order if they're numbers, or something else. For the most part, the exact ordering relation isn't very important. As long as we have a way to compare two items and find out which comes first (or that they're equal, sometimes) it doesn't matter what the details of the comparison are. To make things simple, in this chapter I'll assume we're always sorting numbers.
Because the length of time per comparison depends on the nature of the things being compared, and because that length isn't really part of what distinguishes one sorting algorithm from another, analyses of the time taken by a sorting program are usually expressed not in terms of seconds but in terms of number of comparisons. This measure also eliminates the effect of one computer being faster than another. To help make such measurements, we'll compare two numbers using this procedure:
to lessthanp :a :b if not namep "comparisons [make "comparisons 0] make "comparisons :comparisons+1 output :a < :b end
Of course, if we want to use > or = comparisons in a
sorting algorithm, we should write analogous procedures for those. But in
fact I'll only need lessthanp for the algorithms I'm going to show you.
After trying out a sort program, we can find out how many comparisons it
made using this convenient little tool:
to howmany print :comparisons ern "comparisons end
After telling us the number of comparisons, this procedure erases the counter variable to prepare for the next experiment.
If you haven't studied sort algorithms before, it will be a good exercise
for you to invent one yourself before you continue. Your procedure
sort should take a list of numbers as input, and should output a list of
the same numbers in order from smallest to largest.
? show sort [5 20 3 5 18 9] [3 5 5 9 18 20]
Notice that it's allowable for two (or more) equal numbers to appear in the input.
So that we can compare different algorithms fairly, we should try them on the same input data. You can make a list of 100 random numbers this way:
make "list cascade 100 [fput random 100 ?] []
You should try out both your sort procedures and mine on your random list. In case you want to try your algorithm on my data, to compare the exact numbers of comparisons needed, here is the list I used:
[11 41 50 66 41 61 73 38 2 94 43 55 24 1 77 77 13 2 93 35 43 69 9 46 88 20 43 73 11 74 69 33 28 4 5 1 15 17 13 94 88 42 12 31 67 42 30 30 13 91 31 8 55 6 31 84 57 50 50 31 36 52 5 12 10 19 69 0 9 81 62 14 39 54 45 72 18 47 48 35 76 44 77 34 75 52 61 86 34 44 64 53 25 39 4 55 55 54 53 64]
Notice in passing that this is a list of 100 random numbers, but not a list of the first 100 numbers in random order. Some numbers, like 43, appear more than once in the list, while others don't appear at all. This is perfectly realistic for numbers that occur in real life, although of course some situations give rise to lists of unique items.
Although there are many known sorting algorithms, most fall into two main groups. There are the ones that order the input items one at a time and there are the ones that divide the problem into roughly equal-sized smaller problems. I'll show you one of each. Within a group, the differences between algorithms have to do with details of exactly how the problem is divided into pieces, what's where in computer memory, and so on. But these details are generally much less important than the basic division between the two categories. If you took my advice and wrote your own sort procedure, and if you hadn't studied sorting before, the one you wrote is almost certainly in the first category.
My sample algorithm in the first group is a selection sort. Expressed in words, the algorithm is this: First find the smallest number, then find the next smallest, and so on. This idea can be put in recursive form; the output from the procedure should be a list whose first member is the smallest number and whose remaining elements are the sorted version of the other numbers. I'll show you two versions of this algorithm: first a straightforward but inefficient one, and then a version that's improved in speed but not quite so obvious. Here's the first version:
to ssort :list if emptyp :list [output []] localmake "smallest reduce "min :list output fput :smallest (ssort remove.once :smallest :list) end to remove.once :item :list if equalp :item first :list [output butfirst :list] output fput first :list (remove.once :item butfirst :list) end
In this version of ssort, we start by finding the
smallest number in the list. Then we remove that number from the
list, sort what's left, and put the smallest number back at the front
of the sorted list. The only slight complication is that I had to
write my own variant of remove that, unlike the standard Berkeley
Logo library version, removes only one copy of the chosen number from
the list, just in case the same number appears more than once.
By using min to find the smallest number, I've interfered with
my goal of counting the number of comparisons, but I didn't worry about
that because I'm about to rewrite ssort anyway. The problem is
that this version goes through the list of numbers twice for each
invocation, first to find the smallest number and then again to remove
that number from the list that will be used as input to the recursive
call. The program will be much faster if it does the finding and the
removing all at once. The resulting procedure is a little harder to
read, but it should help if you remember that it's trying to do the same
job as the original version.
to ssort :list if emptyp :list [output []] output ssort1 (first :list) (butfirst :list) [] end to ssort1 :min :in :out if emptyp :in [output fput :min ssort :out] if lessthanp :min (first :in) ~ [output ssort1 :min (butfirst :in) (fput first :in :out)] output ssort1 (first :in) (butfirst :in) (fput :min :out) end
Ssort is invoked once for each time a smallest number must
be found. For each of those iterations, ssort1 is invoked once for
each member of the still-unsorted list; the numbers in the list are moved
from :in to :out except that the smallest-so-far is singled out
in :min.
Suppose we try out ssort on our list of 100 numbers. How many
comparisons will be needed? To find the smallest of 100 numbers we have to
make 99 comparisons; the smallest-so-far must be compared against each of
the remaining ones. To find the next smallest requires 98 comparisons, and
so on. Finally we have two numbers remaining to be sorted and it takes one
comparison to get them in order. The total number of comparisons is
It makes no difference what order the numbers were in to begin with, or
whether some of them are equal, or anything else about the input data. It
takes 4950 comparisons for ssort to sort 100 numbers, period. You can
try out the program on various lists of 100 numbers to make sure I'm right.
In general, if we want to sort a list of length n with ssort the
number of comparisons required is the sum of the integers from 1 to n−1.
It turns out that there is a closed form definition for this sum:
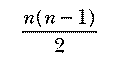
Selection sort uses these three steps:
| • | Pull out the smallest value. | |
|---|---|---|
| • | Sort the other values. | |
| • | Put the smallest one at the front. |
It's the first of those steps that does the comparisons. A similar but different algorithm is insertion sort, which defers the comparisons until the last step:
| • | Pull out any old value (such as the first).
| |
|---|---|---|
| • | Sort the other values. | |
| • | Put the chosen one where it belongs, in order. |
Try writing a procedure isort to implement this
algorithm. How many comparisons does it require? You'll find that
for this algorithm the answer depends on the input data. What is the
smallest possible number of comparisons? The largest number? What
kinds of input data give rise to these extreme values?
There is one fundamental insight behind all methods for sorting with fewer
comparisons: Two small sorting jobs are faster than one large one.
Specifically, suppose we have 100 numbers to sort. Using ssort
requires 4950 comparisons. Instead, suppose we split up the 100 numbers
into two groups of 50. If we use ssort on each group, each will
require 1225 comparisons; the two groups together require twice that, or
2450 comparisons. That's about half as many
comparisons as the straight ssort of 100 numbers.
But this calculation underestimates how much time we can save using this insight, because the same reasoning applies to each of those groups of 50. We can split each into two groups of 25. Then how many comparisons will be required altogether?
The basic idea we'll use is to pick some number that we think is likely to
be a median value for the entire list; that is, we'd like half the numbers
to be less than this partition value and half to be greater. There are many
possible ways to choose this partition value; I'm going to take the average
of the first and last numbers of the (not yet sorted!) input. Then we run
through the input list, dividing it into two smaller pieces by comparing
each number against the partition value. (Notice that ssort compares
pairs of numbers within the input list; the partition sort compares one
number from the list against another number that might or might not itself
be in the list.) We use the same technique recursively to sort each of the
two sublists, then append the results.
Note the similarities and differences between this selection sort algorithm:
| • | Pull out the smallest value. | |
|---|---|---|
| • | Sort the other values. | |
| • | Put the smallest one at the front. |
and the following partition sort algorithm:
| • | Divide the input into the small-value half and the large-value half. | |
|---|---|---|
| • | Sort each half separately. | |
| • | Put the sorted small values in front of the sorted large ones. |
Again, I'll write this program more than once, first in an overly simple version and then more realistically. Here's the simple one:
to psort :list
if (count :list) < 2 [output :list]
localmake "split guess.middle.value :list
output sentence psort filter [? < :split] :list ~
psort filter [not (? < :split)] :list
end
to guess.middle.value :list
output ((first :list) + (last :list)) / 2
end
To minimize the number of comparisons, we want to split the input list
into two equal-size halves. It's important to note that this program
is only guessing about which value of :split would achieve that
balanced splitting. You may wonder why I didn't take the average of
all the numbers in the list. There are two reasons. One is that that
would add a lot of time to the sorting process; we'd have to look at
every number to find the average, then look at every number again to do
the actual splitting. But a more interesting reason is that the average
isn't quite what we want anyway. Suppose we are asked to sort this
list of numbers:
[3 2 1000 5 1 4]
The average of these numbers is about 169. But if we use that value as the split point, we'll divide the list into these two pieces:
[3 2 5 1 4] and [1000]
Not a very even division! To divide this list of six values into two equal pieces, we'd need a split point of 3 ½. In general, what we want is the median value rather than the average value. And if you think about it, you pretty much have to have the numbers already sorted in order to find the median.* So we just try to make a good guess that doesn't take long to compute.
*That isn't quite true; there is a clever algorithm that can find the median after only a partial sorting of the values. But it's true enough that we can't use a sorting algorithm whose first step requires that we've already done some sorting.
Just as in the case of selection sort, one problem with this simple program
is that it goes through the input list twice, once for each of the calls to
filter. And the call to count in the end test adds a third walk
through the entire list. Here's a version that fixes those inefficiencies:
to psort :list if emptyp :list [output []] if emptyp butfirst :list [output :list] localmake "split ((first :list) + (last :list)) / 2 output psort1 :split :list [] [] end to psort1 :split :in :low :high if emptyp :in [output sentence (psort :low) (psort :high)] if lessthanp first :in :split ~ [output psort1 :split (butfirst :in) (fput first :in :low) :high] output psort1 :split (butfirst :in) :low (fput first :in :high) end
This version of psort has one good attribute and one bad
attribute. The good attribute is that it's very cleanly organized. You can
see that it's the job of psort to choose the partition value and the
job of psort1 to divide the list in two parts based on comparisons
with that value. The bad attribute is that it doesn't quite work as
it stands.
As for any recursive procedure, it's important that the input get smaller
for each recursive invocation. If not, psort could end up invoking
itself over and over with the same input. It's very easy to see that
ssort avoids that danger, because the input list is shorter by exactly one
member for each recursive invocation. But psort divides its input
into two pieces, each of which ought to be about half the length of the
original if we're lucky. We're lucky if the partition value we choose is,
in fact, the median value of the input list. If we're less lucky, the two
parts might be imbalanced, say ¼ of the members below the partition and
¾ of them above it. Can we be so unlucky that all of
the input numbers are on the same side of the partition? See if you can
think of a case in which this will happen.
The partition value is chosen as the average of two members of the input
list. If those two members (the first and last) are unequal, then one of
them must be less than the partition value and the other greater. So there
will be at least one number on each side of the partition. But if the two
averaged numbers are equal, then the partition value will be equal to both
of them. Each of them will be put in the high bucket. If all the
other numbers in the list are also greater than or equal to the partition,
then they'll all end up in the high bucket, and nothing will be
accomplished in the recursion step. The simplest failing example is trying
to sort a list of numbers all of which are equal, like
? show psort [4 4 4 4 4]
We could take various approaches to eliminating this bug. See how many ways you can think of, and decide which you like best, before reading further.
Since the problem has to do with the choice of partition value, you could imagine using a more complicated means to select that value. For example, you could start with the first member of the input list, then look through the list for another member not equal to the first. When you find one, average the two of them and that's the partition value. If you get all the way to the end of the list without finding two unequal members, declare the list sorted and output it as is. The trouble with this technique is that many extra comparisons are needed to find the partition value. Those comparisons don't really help in ordering the input, but they do add to the time taken just as much as the "real" comparisons done later.
Another approach is to say that since the problem only arises if the first and last input members are equal, we should treat that situation as a special case. That is, we'll add an instruction like
if equalp first :list last :list [...]
Again, this approach adds a comparison that doesn't really help to sort the file, although it's better than the first idea because it only adds one extra comparison per invocation instead of perhaps several.
A more straightforward approach that might seem to make the program more
efficient, rather than less, is to divide the list into three
buckets, low, high, and equal. This way, the problem gets
shorter faster, since the equal bucket doesn't have to be sorted
recursively; it's already in order. The trouble is that it takes two
comparisons, one for equality and one for lessthanp, to know how to
direct each list member into a three-way split. Some computers can compare
numbers once and branch in different directions for less, equal, or greater;
one programming language, Fortran, includes that kind of three-way branching
through an "arithmetic IF" statement that accepts different instructions
for the cases of a given quantity being less than, equal to, or greater than
zero. But in Logo we'd have to say
if lessthanp first :in :split [...] if equaltop first :in :split [...]
with two comparisons for each list member. (I'm imagining that
equaltop would keep track of the number of comparisons just as
lessthanp does.)
What I chose was to do the first lessthanp test for the list in
psort instead of psort1, and use it to ensure that either the first
or the last member of the list starts out the low bucket.
to psort :list if emptyp :list [output []] if emptyp butfirst :list [output :list] localmake "split ((first :list) + (last :list)) / 2 if lessthanp first :list :split ~ [output psort1 :split (butfirst :list) (list first :list) []] output psort1 :split (butlast :list) (list last :list) [] end
Psort1 is unchanged.
How many comparisons should psort require to sort 100 numbers? Unlike
ssort, its exact performance depends on the particular list of numbers
given as input. But we can get a general idea. The first step is to divide
the 100 numbers into two buckets, using 100 comparisons against the
partition value. The second step divides each of the buckets in two again.
We can't say, in general, how big each bucket is; but we do know that each
of the original 100 numbers has to be in one bucket or the other. So each
of 100 numbers will participate in a comparison in this second round also.
The same argument applies to the third round, and so on. Each round
involves 100 comparisons. (This isn't quite true toward the end of the
process. When a bucket only contains one number, it is considered sorted
without doing any comparisons. So as the buckets get smaller, eventually
some of the numbers "drop out" of the comparison process, while others are
still not in their final position.)
Each round involves 100 comparisons, more or less. How many rounds are there? This is where the original ordering of the input data makes itself most strongly felt. If we're lucky, each round divides each bucket exactly in half. In that case the size of the buckets decreases uniformly:
round size 1 100 2 50 3 25 4 12,13 5 6,7 6 3,4 7 1,2
There is no round 8, because by then all of the buckets would be of length 1 and there is no work left to do. So if all goes well we'd expect to make about 700 comparisons, really a little less because by round 7 some of the numbers are already in length-1 buckets. Maybe 650?
What is the worst case? That would be if each round divides the
numbers into buckets as unevenly as possible, with one number in one bucket
and all the rest in the other. In that case it'll take 99 rounds to get all
the numbers into length-1 buckets. You may be tempted to estimate 9900
comparisons for that situation, but in fact it isn't quite so bad, because
at each round one number falls into a length-1 bucket and drops out of the
sorting process. So the first round requires 100 comparisons, but the
second round only 99, the third 98, and so on. This situation is very much
like the way ssort works, and so we'd expect about 5000 comparisons.
Now try some experiments. Try psort on your random list, then try to
find input lists that give the best and worst possible results.
Psort required 725 comparisons for my random list. That's somewhat
more than we predicted for the best case, but not too much more.
Psort seems to have done pretty well with this list. The simplest
worst-case input is one in which all the numbers are the same; I said
make "bad cascade 100 [fput 20 ?] []
to make such a list. Psort required 5049 comparisons to
sort this list, slightly worse than ssort at 4950 comparisons.
What would a best-case input look like? It would divide evenly at each stage; that is, the median value at each stage would be the average of the first and last values. The simplest list that should meet that criterion is a list of all the numbers from 1 to 100 in order:
make "inorder cascade 100 [lput # ?] []
(Or you could use the reverse trick discussed earlier, but
for only 100 numbers it didn't seem worth the extra typing to me.) Using
psort to sort this list should require, we said, somewhere around 650
to 700 comparisons. In fact it took 734 comparisons when I tried it,
slightly more than my randomly ordered list (725 comparisons).
Even 734 comparisons isn't terrible by any means, but when an algorithm
performs worse than expected, a true algorithm lover wants to know why.
Test cases like these can uncover either inefficiencies in the fundamental
algorithm or else ways in which the actual computer program doesn't live up
to the algorithm as described in theoretical language. If we could "tune
up" this program to sort :inorder in fewer than 700 comparisons, the
change might well improve the program's performance for any input. See if
you can figure out what the problem is before reading further. You can try
having psort print out its inputs each time it's called, as a way to
help gather information.
Here's a very large hint. I tried using the original version of
psort, before fixing the bug about the recursion sometimes leaving all the
numbers in one basket, and it sorted :inorder in only 672 comparisons.
(I knew the bug wouldn't make trouble in this case because none of the
numbers in this particular input list are equal.) Can you devise a better
psort that both works all the time and performs optimally for the
best-case input?
This partition sorting scheme is essentially similar to a very well-known
algorithm named quicksort, invented by C. A. R. Hoare.
Quicksort includes many improvements over this algorithm, not primarily in
reducing the number of comparisons but in decreasing the overhead time by,
for example, exchanging pairs of input items in their original memory
locations instead of making copies of sublists. Quicksort also switches to
a more straightforward ssort-like algorithm for very small input lists,
because the benefit of halving the problem is outweighed by the greater
complexity. (In fact, for a two-item input, ssort makes one
comparison and psort two.)
Here's the partition sort algorithm again:
| • | Divide the input into the small-value half and the large-value half. | |
|---|---|---|
| • | Sort each half separately. | |
| • | Put the sorted small values in front of the sorted large ones. |
The idea of cutting the problem in half is also used in the following algorithm, called mergesort:
| • | Divide the input arbitrarily into two equal size pieces. | |
|---|---|---|
| • | Sort each half separately. | |
| • | Merge the two sorted pieces by comparing values. |
In a way, mergesort is to partition sort as insertion sort is to selection sort. Both insertion sort and mergesort defer the comparisons of numbers until the final step of the algorithm.
There is one important way in which mergesort is better than partition sort. Since mergesort doesn't care how the input values are separated, we can ensure that the two pieces are each exactly half the size of the input. Therefore, the number of comparisons needed is always as small as possible; there are no bad inputs. Nevertheless, quicksort is more widely used than mergesort, because the very best implementations of quicksort seem to require less overhead time, for the average input, than the best implementations of mergesort.
If you want to write a mergesort program, the easiest way to divide a list into two equal pieces is to select every other member, so the odd-position members are in one half and the even-position members in the other half.
I've mentioned that the complete quicksort algorithm includes several optimization strategies to improve upon the partition sort I've presented here. How important are these strategies? How much does overhead contribute to the cost of a program? I did some experiments to investigate this question.
First I timed psort and ssort with inputs of length 300.
Here are the results:
| program | comparisons | time | comparisons | per second | |
|---|---|---|---|---|---|
psort | 2940 | 29 seconds | 100 | ||
ssort | 44850 | 313 seconds | 143 |
Ssort seems to have much less overhead, since it can do
more comparisons per second than psort. Nevertheless, psort
always seems to be faster, for every size input I tried. The number
of comparisons outweighs the overhead. (By the way, these numbers don't
measure how fast the computer can compare two numbers! A typical computer
could perform more than a million comparisons per second, if only
comparisons were involved. Most of the time in these experiments is
actually going into the process by which the Logo interpreter figures out
what the instructions in the program mean. Because Berkeley Logo is
an interpreter, this figuring-out process happens every time an instruction
is executed. By contrast, I tried ssort on a list of length 300 in
Object Logo, a compiled version in which each instruction is figured out
only once, and the total time was 3.6 seconds.)
I wanted to give local optimization the best possible chance to win the
race, and so I decided to make selection sort as fast as I could, and
partition sort as slow as I could. I modified ssort to use the
Logo primitive lessp for comparison instead of doing the extra
bookkeeping of lessthanp, and I replaced psort with this
implementation:
to slowsort :list
if (count :list) < 2 [output :list]
localmake "split (reduce "sum :list)/(count :list)
output (sentence slowsort filter [? < :split] :list
filter [? = :split] :list
slowsort filter [? > :split] :list)
end
This version examines every member of the input list six times
on each recursive call! (Count is invoked twice; reduce
looks at every list member once; and filter is called three times
to do the actual partition.) Under these conditions I was able to get
ssort to win the race, but only for very small inputs:
| program | 20 numbers | 100 numbers | 300 numbers | |||
|---|---|---|---|---|---|---|
slowsort | 2.7 seconds | 18 seconds | 63 seconds | |||
ssort | 1.2 seconds | 20 seconds | 182 seconds |
Ssort wins when sorting 20 numbers, but both programs
take less than three seconds. For 100 numbers, slowsort is
already winning the race, and its lead grows as the input list grows.
This is a common pattern: For small amounts of data, when the program is
fast enough no matter how you write it, local optimization can win the race,
but once the problem is large enough so that you actually care about
efficiency, choosing a better overall algorithm is always more important.
(Of course the very best results will come from choosing a good algorithm
and optimizing the program locally.)
What does "a better algorithm" actually mean? How do we measure the quality of an algorithm? We've made a good start by counting the number of comparisons required for our two sorting algorithms, but there is a formal notation that can make the issues clearer.
Earlier I said that for a list of n numbers, ssort makes
comparisons. But in a sense this tells us more than we want to
know, like saying that a certain program took 1,243,825 microseconds instead
of saying that it took somewhat over a second. The important thing to say
about ssort is that the number of comparisons is roughly proportional
to n2; that is, doubling the size of the input list will quadruple the
time needed to sort the list. More formally, we say that the time required
for selection sorting is O(n2), pronounced "big-oh of n2" or
"order n2." This is an abbreviation for the statement, "for large enough n,
the time is bounded by n2 times a constant."
The part about "for large enough n" is important because the running
time for some algorithm might, for example, involve a large constant setup
time. For small n that setup time might contribute more to the overall
time required than the part of the algorithm proportional* to n2, but
once n becomes large enough, the n2 part will overtake any constant.
*Strictly speaking, the fact that an algorithm's time requirement is O(n2) doesn't mean that it's even approximately proportional to n2, because O(...) only establishes an upper bound. The time requirement could be proportional to n, which would be better than n2, and still be O(n2). But usually people use O(...) notation to mean that no smaller order of growth would work, even though there's an official notation with that meaning, Θ(n2), pronounced "big theta."
I'd like to have a similar representation, O(something), for the
number of comparisons used by psort in the typical case. We said that
for 100 numbers, each round of sorting involves about 100 comparisons, and
the number of rounds required is the number of times you have to divide 100
by 2 before you get down to 1, namely between 6 and 7. The number of
comparisons expected is the product of these numbers. In the general case,
the first number is just n. But what is the general formula for the
number of times you have to divide n by 2 to get 1? The answer is log2 n. For example, if we had 128 numbers in the list instead of 100, we would
require exactly 7 rounds (in the best case) because 27 = 128 and so
log2 128 = 7. (By the way, log2 100 ≅ 6.65, so the
theoretical best case for 100 numbers is 665 comparisons.)
In general, all the obvious sorting algorithms are O(n2) and all the
clever ones are O(n log n).* (I don't
have to say O(n log2 n) because the difference between logarithms to
different bases is just multiplication by a constant factor, which doesn't
count in O(...) notation, just as I don't have to worry about the fact
that the formula for ssort comparisons is nearer n2/2 than n2.)
By the way, I haven't really proven that psort is O(n log n)
in the typical case, only that it is in the best case. It's much
harder to prove things about the typical (or average) performance of any
sorting algorithm, because what is an "average" input list? For some
algorithms there is no proven formula for the average run time, but only the
results of experiments with many randomly chosen lists.
*Don Knuth has written an O(n3) sort program, just as an example of especially bad programming.
An O(n) algorithm is called linear and an O(n2) one
quadratic. O(n log n) is in between those, better than quadratic but not
as good as linear. What other orders of growth are commonly found? As one
example, the pre-memoized procedures for the t and simplex
functions in Chapter 2 have time requirements that are O(2n); these are
called exponential algorithms. This means that just adding one
to n makes the program take twice as long! The experimental results I gave
earlier agree with this formula: simplex 10 took 80 seconds, while
simplex 12 took 5 ½ minutes, about four times as long.
Simplex 16 would take over an hour. (Start with 80 seconds, and
double it six times.) The memoized versions in this chapter are O(n2)
(can you prove that?), which is much more manageable. But for some
really hard problems there is no known way to make them any
faster than O(2n);
problems like that are called intractable, while ones that
are merely polynomial--O(ni) for any constant i--are called
tractable.
One of the reasons computers are so useful is that they can contain a tremendous amount of information. An important part of writing a large computer program is figuring out how to organize the information used in the program. Most of the time, a program doesn't have to deal with a bunch of unrelated facts, like "Tomatoes are red" and "7 times 8 is 56." Instead there will be some kind of uniformity, or natural grouping, in the information a program uses.
We'll see, too, that the data structures you choose for your program affect the algorithms available to you. Organizing your data cleverly can reduce the execution time of your procedures substantially.
Why should there be different kinds of organization? It might help to look at some analogies with data structures outside of computers. First of all, think about your personal address book. It probably has specific pages reserved for each letter of the alphabet. Within a letter, the names and addresses of people starting with that letter are arranged in no particular order; you just add a new person in the first free space on the page.
Now think about the printed telephone directory for your city. In this case the names are not arranged randomly within each letter; they're in strict alphabetical order. In computer science terminology, the printed directory is a sorted list, while your personal directory is a hash table.
Obviously, if the entries in the printed directory weren't in order it would take much too long to find an address. You can get away with random ordering within each letter in your personal directory because you know a small enough number of people that it doesn't take too long to look through each one. But you probably do know enough people to make the separate page for each letter worthwhile, even though the page for Q may be practically empty. By using separate pages for each letter, with unused slots on each page reserved for expansion, you are spending space to buy time. That is, your address book is bigger than it would be if it were just one long list, but looking up a number is faster this way. This tradeoff between time and space is typical of computer programming problems also.
Why don't you keep your personal directory in strict alphabetical order, like the printed phone book? If you did that, looking up a number would be even faster. The problem is that adding a new number would be terribly painful; you'd have to erase all the names on the page below where the new name belongs and rewrite each of them one line below where it was.* In this case there is a tradeoff between storage time and retrieval time; you pay a small price in retrieval time to avoid a large price in storage time. This, too, is a common aspect of data structure design in computer programs.
*Why doesn't the phone company have to do that whenever they get a new customer? The answer is that they maintain the directory information in two forms. The printed directory is the external representation, used only for looking up information; inside their computers they use an internal representation that allows for easier insertion of new entries.
Other kinds of real-life data structures also have computer analogues. If your desk looks like mine, with millions of little slips of paper all over the place, it is what computer scientists call a heap.* This might be an appropriate data structure for those cases in which the program must deal with a large mass of unrelated facts. On the other hand, in a large business office there will be a hierarchical filing system. A file cabinet labeled "Personnel Records" might contain a drawer labeled "Inactive A-H"; that drawer would contain a file folder for each former employee whose name starts with an appropriate letter. This kind of hierarchy might be represented as a tree in a computer program.
*Unfortunately, there are two things called a "heap" in computer science. I'm thinking of the storage allocation heap, not the special tree structure used in the "heapsort" algorithm.
We've used the idea of trees before. In Volume 1, the program to solve
pitcher pouring problems was designed in terms of a tree of possible
solution steps, although that tree was not represented as actual data
in the program. In Volume 2, I wrote tree.map as an example of a
higher order function operating on trees in which the leaf nodes are
words and the branch nodes are phrases. In this chapter we'll work
toward a general representation of trees as an abstract data type.
Here is a hierarchical grouping of some of the world's cities:
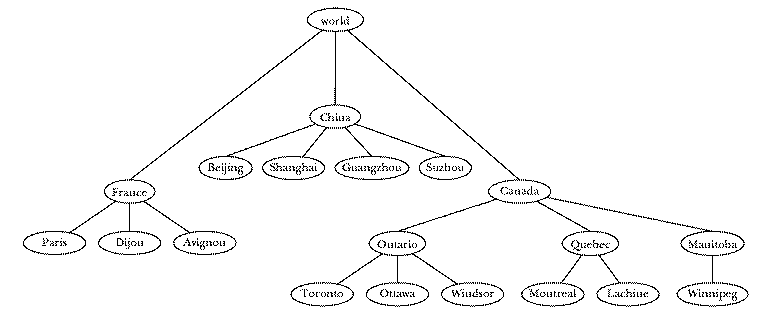
Recall that a diagram like this is called a tree because it resembles a real
tree turned upside-down. Each place where a word or phrase appears in the
tree is called a node. At the top of the diagram is the
root node (world). The lines between nodes are called
branches. The cities, which do not have branches extending below them,
are called leaf nodes. The in-between nodes, the countries
and provinces, are called branch nodes. (The root node is
also considered a branch node since it, too, has branches below it.) This
tree tells us that Toronto is in Ontario, which is in Canada, which is in the
world.
A tree is a very general data structure because its shape is very flexible. For example, in the part of this tree that represents Canada I've included a level of tree structure, representing the provinces, that isn't included in the subtree that represents France. As we'll see later, some algorithms deal with restricted categories of trees. For example, a binary tree is a tree with at most two branches below each branch node.
So far this data structure is just a graphic representation on paper. There are many ways in which a tree can be implemented in a computer program. Let's say that I want to represent the tree of cities in a computer so that I can ask questions from this data base. That is, I'd like to write a program that will allow interactions like
? show locate "Montreal [world Canada Quebec Montreal]
Let's pick a particular way to represent a tree in Logo. (I
should warn you that later in the chapter I'm going to invent different
representations, but I want to start with a simple one to meet our
immediate needs. So what you're about to see is not the final version of
these procedures.) Here's
the way I'm going to do it: Each branch node will be represented as a Logo
variable whose name is the name of the node, containing as its value a list
of the names of the nodes immediately below it. For example, this tree will
include a variable named France with the value
[Paris Dijon Avignon]
A leaf node is just a word that appears in a node list but isn't
the name of a variable. For a branch node, thing of the node's name
will provide a list of the names of its children. I can set up the tree
with this procedure:
to worldtree make "world [France China Canada] make "France [Paris Dijon Avignon] make "China [Beijing Shanghai Guangzhou Suzhou] make "Canada [Ontario Quebec Manitoba] make "Ontario [Toronto Ottawa Windsor] make "Quebec [Montreal Lachine] make "Manitoba [Winnipeg] end
In principle, locate is a lot like filter, in the sense that
we're looking through a data structure for something that meets a given
condition. But the implementation is a bit trickier than looking through
a sequential list, because each invocation gives rise to several recursive
invocations (one per child), not merely one recursive invocation as usual.
The program will be easier to understand if we introduce the term
forest, which means a list of trees.
to locate :city output locate1 :city "world end to locate1 :city :subtree if equalp :city :subtree [output (list :city)] if not namep :subtree [output []] localmake "lower locate.in.forest :city (thing :subtree) if emptyp :lower [output []] output fput :subtree :lower end to locate.in.forest :city :forest if emptyp :forest [output []] localmake "child locate1 :city first :forest if not emptyp :child [output :child] output locate.in.forest :city butfirst :forest end ? show locate "Shanghai [world China Shanghai] ? show locate "Montreal [world Canada Quebec Montreal]
Once we've set up this data base, we can write procedures to ask it other kinds of questions, too.
to cities :tree if not namep :tree [output (list :tree)] output map.se [cities ?] thing :tree end ? show cities "France [Paris Dijon Avignon] ? show cities "Canada [Toronto Ottawa Windsor Montreal Lachine Winnipeg]
There's a problem with the representation I've chosen for this tree. Suppose we want to expand the data base to include the city of Quebec. This city is in the province of Quebec, so all we have to do is add the name to the appropriate list:
make "Quebec [Montreal Quebec Lachine]
If you try this, however, you'll find that locate and
cities will no longer work. They'll both be trapped in infinite loops.
The problem with this program can't be fixed just by changing the program. It's really a problem in the way I decided to represent a tree. I said, "a leaf node is just a word that appears in a node list but isn't the name of a variable." But that means there's no way to allow a leaf node with the same name as a branch node. To solve the problem I have to rethink the conventions I use to represent a tree.
Being lazy, I'd like to change as little as possible in the program, so I'm
going to try to find a new representation as similar as possible to the old
one. Here's my idea: In my mind I associate a level with each
node in the tree. The node world is at level 1, France and
Canada at level 2, and so on. The names of the variables used to hold
the contents of a node will be formed from the node name and the level:
world1, France2, Ontario3, and so on. This solves the
problem because the node for Quebec province will be a branch node by virtue
of the variable Quebec3, but the node for Quebec city will be a leaf
node because there will be no Quebec4 variable.
As it turns out, though, I have to change the program quite a bit to make
this work. Several procedures must be modified to take the level number
as an additional input. Also, since the variable that holds the information
about a place is no longer exactly named with the place's name, cities
has some extra work to do, just to find the node whose cities we want to
know. It can almost use locate for this purpose, but with a slight
wrinkle: If we ask for the cities in Quebec, we mean Quebec province, not
Quebec city. So we need a variant of locate that finds the node
highest up in the tree with the desired place name. I gave subprocedure
locate1 an extra input, named highest, that's true if we want
the highest matching tree node (when called from cities) or false
if we want a matching leaf node (when called from locate).
to worldtree
make "world1 [France China Canada]
make "France2 [Paris Dijon Avignon]
make "China2 [Beijing Shanghai Guangzhou Suzhou]
make "Canada2 [Ontario Quebec Manitoba]
make "Ontario3 [Toronto Ottawa Windsor]
make "Quebec3 [Montreal Quebec Lachine]
make "Manitoba3 [Winnipeg]
end
to locate :city
output locate1 :city "world 1 "false
end
to locate1 :city :subtree :level :highest
localmake "name (word :subtree :level)
if and :highest equalp :city :subtree [output (list :city)]
if not namep :name ~
[ifelse equalp :city :subtree
[output (list :city)]
[output []]]
localmake "lower locate.in.forest :city (thing :name) :level+1 :highest
if emptyp :lower [output []]
output fput :subtree :lower
end
to locate.in.forest :city :forest :level :highest
if emptyp :forest [output []]
localmake "child locate1 :city first :forest :level :highest
if not emptyp :child [output :child]
output locate.in.forest :city butfirst :forest :level :highest
end
to cities :tree
localmake "path locate1 :tree "world 1 "true
if emptyp :path [output []]
output cities1 :tree count :path
end
to cities1 :tree :level
localmake "name (word :tree :level)
if not namep :name [output (list :tree)]
output map.se [(cities1 ? :level+1)] thing :name
end
? show locate "Quebec
[world Canada Quebec Quebec]
? show cities "Canada
[Toronto Ottawa Windsor Montreal Quebec Lachine Winnipeg]
This new version solves the Quebec problem. But I'm still not satisfied.
I'd like to add the United States to the data base. This is a country whose
name is more than one word. How can I represent it in the tree structure?
The most natural thing would be to use a list: [United States].
Unfortunately, a list can't be the name of a variable in Logo. Besides,
now that I've actually written the program using this representation I see
what a kludge it is!
My next idea for representing a tree is to abandon the use of a separate
variable for each node; instead I'll put the entire tree in one big list.
A node will be a list whose first is the datum at that node and whose
butfirst is a list of children of the node. So the entire tree will be
represented by a list like this:
[world [France ...] [[United States] ...] [China ...] [Canada ...]]
The datum at each node can be either a word or a list.
But this time I'm going to be smarter than before. I'm going to recognize
that the program I'm writing should logically be separated into two parts:
the part that implements the tree data type, and the part that uses
a tree to implement the data base of cities. If I write procedures like
locate and cities in terms of general-purpose tree subprocedures
like leafp, a predicate that tells whether its input node is a leaf
node, then I can change my mind about the implementation of trees (as I've
done twice already) without changing that part of the program at all.
I'll start by implementing the abstract data type. I've decided that a tree
will be represented as a list with the datum of the root node as its
first and the subtrees in the butfirst. To make this work I need
selector procedures:
to datum :node output first :node end to children :node output butfirst :node end
and a constructor procedure to build a node out of its pieces:
to tree :datum :children output fput :datum :children end
Selectors and constructors are the main procedures needed to define any data
structure, but there are usually some others that can be useful. For the
tree, the main missing one is leafp.
to leafp :node output emptyp children :node end
Now I can use these tools to write the data base procedures.
to locate :city
output locate1 :city :world "false
end
to locate1 :city :subtree :wanttree
if and :wanttree (equalp :city datum :subtree) [output :subtree]
if leafp :subtree ~
[ifelse equalp :city datum :subtree
[output (list :city)]
[output []]]
localmake "lower locate.in.forest :city (children :subtree) :wanttree
if emptyp :lower [output []]
output ifelse :wanttree [:lower] [fput (datum :subtree) :lower]
end
to locate.in.forest :city :forest :wanttree
if emptyp :forest [output []]
localmake "child locate1 :city first :forest :wanttree
if not emptyp :child [output :child]
output locate.in.forest :city butfirst :forest :wanttree
end
to cities :name
output cities1 (finddatum :name :world)
end
to cities1 :subtree
if leafp :subtree [output (list datum :subtree)]
output map.se [cities1 ?] children :subtree
end
to finddatum :datum :tree
output locate1 :name :tree "true
end
Once again, cities depends on a variant of locate that
outputs the subtree below a given name, instead of the usual locate
output, which is a list of the names on the path from world down to
a city. But instead of having cities call locate1 directly,
I decided that it would be more elegant to provide a procedure
finddatum that takes a datum and a tree as inputs, whose output is the
subtree below that datum.
In cities1, the expression
(list datum :subtree)
turns out to be equivalent to just :subtree for the case of
a leaf node. (It is only for leaf nodes that the expression is evaluated.)
By adhering to the principle of data abstraction I'm making the program work
a little harder than it really has to. The advantage, again, is that this
version of cities will continue working even if we change the
underlying representation of trees. The efficiency cost is quite low;
changing the expression to :subtree is a local optimization comparable
to the common subexpression elimination we considered early in the chapter.
I also have to revise the procedure to set up the tree. It's going to
involve many nested invocations of tree, like this:
to worldtree
make "world tree "world
(list (tree "France
(list (tree "Paris [])
(tree "Dijon [])
(tree "Avignon []) ) )
(tree "China
(list ...
and so on. I can shorten this procedure somewhat by inventing an abbreviation for making a subtree all of whose children are leaves.
to leaf :datum
output tree :datum []
end
to leaves :leaves
output map [leaf ?] :leaves
end
to worldtree
make "world
tree "world
(list (tree "France leaves [Paris Dijon Avignon])
(tree "China leaves [Beijing Shanghai Guangzhou Suzhou])
(tree [United States]
(list (tree [New York]
leaves [[New York] Albany Rochester
Armonk] )
(tree "Massachusetts
leaves [Boston Cambridge Sudbury
Maynard] )
(tree "California
leaves [[San Francisco] Berkeley
[Palo Alto] Pasadena] )
(tree "Washington
leaves [Seattle Olympia] ) ) )
(tree "Canada
(list (tree "Ontario
leaves [Toronto Ottawa Windsor] )
(tree "Quebec
leaves [Montreal Quebec Lachine] )
(tree "Manitoba leaves [Winnipeg]) ) ) )
end
? worldtree
? show cities [United States]
[[New York] Albany Rochester Armonk Boston Cambridge Sudbury Maynard
[San Francisco] Berkeley [Palo Alto] Pasadena Seattle Olympia]
? show locate [Palo Alto]
[world [United States] California [Palo Alto]]
So far, so good. But the procedure worldtree just above is very
error-prone because of its high degree of nesting. In the earlier versions
I could create the tree a piece at a time instead of all at once. In a
practical data base system, people should be able to add new information at
any time, not just ask questions about the initial information. That is,
I'd like to be able to say
addchild :world (tree "Spain leaves [Madrid Barcelona Orense])
to add a subtree to the world tree. New nodes should be possible not only at the top of the tree but anywhere within it:
addchild (finddatum "Canada :world) (tree [Nova Scotia] leaves [Halifax])
Most versions of Logo do not provide tools to add a new member to an
existing list. We could write a program that would make a new copy of the
entire tree, adding the new node at the right place in the copy, so that
addchild would take the form
make "world newcopy :world ...
but there are two objections to that. First, it would be quite
slow, especially for a large tree. Second, it would work only if I refrain
from assigning subtrees as the values of variables other than world.
That is, I'd like to be able to say
? make "Canada finddatum "Canada :world ? addchild :Canada (tree [Nova Scotia] leaves [Halifax]) ? show locate "Halifax [world Canada [Nova Scotia] Halifax]
Even though I've added the new node to the tree :Canada, it
should also be part of :world (which is where locate looks)
because :Canada is a subtree of :world. Similarly, I'd like to
be able to add a node to the Canadian subtree of :world and have it
also be part of :Canada. That wouldn't be true if addchild
makes a copy of its tree input instead of modifying the existing tree.
I'm going to solve this problem two ways. In the Doctor project in
Volume 2 of this series, you learned that Berkeley Logo does include
primitive procedures that allow the modification of an existing list
structure. I think the most elegant solution to the addchild problem
is the one that takes advantage of that feature. But I'll also show a
solution that works in any version of Logo, to make the point that list
mutation isn't absolutely necessary; we can achieve the same goals, with
the same efficiency, by other means. First here's the list mutation
version of addchild:
to addchild :tree :child .setbf :tree (fput :child butfirst :tree) end ? make "GB leaf [Great Britain] ? addchild :world :GB ? addchild :GB tree "England leaves [London Liverpool Oxford] ? addchild :GB tree "Scotland leaves [Edinburgh Glasgow] ? addchild :GB tree "Wales leaves [Abergavenny] ? show locate "Glasgow [world [Great Britain] Scotland Glasgow]
Just as tree is a constructor for the tree data type, and
children is a selector, addchild is called a mutator for
this data type. Notice, by the way, that :GB, which was originally
built as a leaf node, can be turned into a branch node by adding children to
it; addchild is not limited to nodes that already have children.
The solution using .setbf is elegant because I didn't have to change
any of the procedures I had already written; this version of addchild
works with the same tree implementation I had already set up. But suppose
we didn't have .setbf or didn't want to use it. (As we'll see shortly,
using list mutators does open up some possible pitfalls.) We can write a
mutator for the tree abstract data type even if we don't have mutators for
the underlying Logo lists! The secret is to take advantage of variables,
whose values can be changed--mutated--in any version of Logo.
To make this work I'm going to go back to a tree representation somewhat like the one I started with, in which each node is represented by a separate variable. But to avoid the problems I had earlier about Quebec and San Francisco, the variable name won't be the datum it contains. Instead I'll use a generated symbol, an arbitrary name made up by the program. (This should sound familiar. I used the same trick in the Doctor project, and there too it was an alternative to list mutation.)
This is where my use of data abstraction pays off. Look how little I have to change:
to tree :datum :children localmake "node gensym make :node fput :datum :children output :node end to datum :node output first thing :node end to children :node output butfirst thing :node end to addchild :tree :child make :tree lput :child thing :tree end
That's it! Leafp, finddatum, locate,
cities, and worldtree all work perfectly without modification,
even though I've made a profound change in the actual representation of
trees. (Try printing :world in each version.)
Addchild is only one of the possible ways in which I might want to
modify a tree structure. If we were studying trees more fully, I'd create
tool procedures to delete a node, to move a subtree from one location in the
tree to another, to insert a new node between a parent and its children, and
so on. There are also many more questions one might want to ask about a
tree. How many nodes does it have? What is its maximum depth?
I've mentioned general tree manipulation tools. There are also still some
unresolved issues about the particular use of trees in the city data base.
For example, although the problem of Quebec city and Quebec province is
under control, what if I want the data base to include Cambridge, England
as well as Cambridge, Massachusetts? What should locate do if given
Cambridge as input?
But instead of pursuing this example further I want to develop another example, in which trees are used for a very different purpose. In the city data base, the tree represents a hierarchy (Sudbury is part of Massachusetts); in the example below, a tree is used to represent an ordering of data, as in the sorting algorithms discussed earlier.
Forget about trees for a moment and consider the general problem of searching through a data base for some piece of information. For example, suppose you want a program to find the city corresponding to a particular telephone area code. That is, I want to be able to say
? print listcity 415 San Francisco
The most straightforward way to do this is to have a list containing code-city pairs, like this:
make "codelist [[202 Washington] [206 Seattle] [212 New York] [213 Los Angeles] [215 Philadelphia] [303 Denver] [305 Miami] [313 Detroit] [314 St. Louis] [401 Providence] [404 Atlanta] [408 Sunnyvale] [414 Milwaukee] [415 San Francisco] [504 New Orleans] [608 Madison] [612 St. Paul] [613 Kingston] [614 Columbus] [615 Nashville] [617 Boston] [702 Las Vegas] [704 Charlotte] [712 Sioux City] [714 Anaheim] [716 Rochester] [717 Scranton] [801 Salt Lake City] [804 Newport News] [805 Ventura] [808 Honolulu]]
This is a list of lists. Each sublist contains one pairing of an area code with a city. We can search for a particular area code by going through the list member by member, comparing the first word with the desired area code. (By the way, in reality a single area code can contain more than one city, and vice versa, but never mind that; I'm trying to keep this simple.) In accordance with the idea of data abstraction, we'll start with procedures to extract the area code and city from a pair.
to areacode :pair output first :pair end to city :pair output butfirst :pair end
The city is the butfirst rather than the last to
accommodate cities with names of more than one word.
The iteration tool find does exactly what's needed, going through a
list member by member until it finds one that matches some criterion:
to listcity :code output city find [equalp :code areacode ?] :codelist end
Time for a little analysis of algorithms. What is the time
behavior of this linear search algorithm as the data base gets
bigger? As for the case of the sorting algorithms, I'll concentrate on the
number of comparisons. How many times is equalp invoked? The best
case is if we're looking for the first code in the list, 202. In this case
only one comparison is made. The worst case is if we're looking for the
last code in the list, 808, or if we're looking for an area code that isn't
in the list at all. This requires 31 comparisons. (That's how many
code-city pairs happen to be in this particular data base.) On the average
this algorithm requires a number of comparisons half way between these
extremes, or 16. As we increase the size of the data base, the number of
comparisons required grows proportionally; this algorithm is O(n).
The area codes in :codelist are in ascending order. If you were
looking through the list yourself, you wouldn't look at every entry one
after another; you'd take advantage of the ordering by starting around the
middle and moving forward or backward depending on whether the area code you
found was too low or too high. That's called a binary search
algorithm. Listcity, though, doesn't take
advantage of the ordering in the list; the pairs could just as well be
jumbled up and listcity would be equally happy.
Binary search works by starting with the median-value area code in the data base. If that's the one we want, we're finished; otherwise we take the higher or lower half of the remaining codes and examine the median value of that subset. One way we could implement that algorithm would be to use a binary tree to represent the code-city pairs:
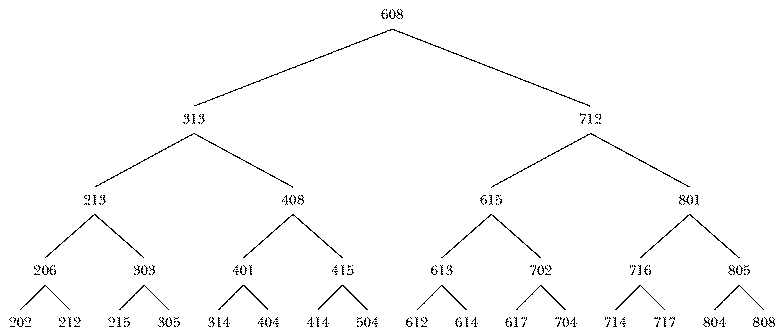
(In this picture I've just shown the area codes, but of course the actual data structure will have a code-city pair at each node.)
We could construct the tree from scratch, using tree and leaves
as I did earlier, but since we already have the pairs in the correct sorted
order it's easier to let the computer do it for us:
to balance :list
if emptyp :list [output []]
if emptyp butfirst :list [output leaf first :list]
output balance1 (int (count :list)/2) :list []
end
to balance1 :count :in :out
if equalp :count 0 ~
[output tree (first :in) (list balance reverse :out
balance butfirst :in )]
output balance1 (:count-1) (butfirst :in) (fput first :in :out)
end
In this program I'm using the trick of building :out using
fput instead of lput and then using reverse to get the
left branch back in ascending order, to make the construction a little
faster.
make "codetree balance :codelist
will generate the tree.
Now we're ready to write treecity, the tree-based search program
analogous to listcity for the linear list.
to treecity :code output city treecity1 :code :codetree end to treecity1 :code :tree if emptyp :tree [output [000 no city]] localmake "datum datum :tree if :code = areacode :datum [output :datum] if :code < areacode :datum [output treecity1 :code lowbranch :tree] output treecity1 :code highbranch :tree end to lowbranch :tree if leafp :tree [output []] output first children :tree end to highbranch :tree if leafp :tree [output []] output last children :tree end ? print treecity 415 San Francisco
Treecity gives the same output as listcity, but it's
faster. At worst it makes two comparisons (for equal and less than) at each
level of the tree. This tree is five levels deep, so if the input area code
is in the tree at all we'll make at most 9 comparisons, compared to 31 for
listcity. The average number is less. (How much less?) The
difference is even more striking for larger data bases; if the number of
pairs is 1000, the worst-case times are 1000 for listcity and 19 for
treecity.
In general the depth of the tree is the number of times you can divide the number of pairs by two. This is like the situation we met in analyzing the partition sort algorithm; the depth of the tree is the log base two of the number of pairs. This is an O(log n) algorithm.
The procedures lowbranch and highbranch are data abstraction at
work. I could have used first children :tree directly in
treecity1, but this way I can change my mind about the representation of
the tree if necessary. In fact, in a practical program I would want to use
a representation that allows a node to have a right child (a
highbranch) without having a left child. Also, lowbranch and
highbranch are written robustly; they give an output, instead of
causing an error, if applied to a leaf node. (That happens if you ask for
the city of an area code that's not in the data base.) I haven't
consistently been writing robust programs in this chapter, but I thought I'd
give an example here.
The efficiency of the tree searching procedure depends on the fact that the tree is balanced. In other words, the left branch of each node is the same size as its right branch. I cheated slightly by starting with 31 area codes, a number that allows for a perfectly balanced tree. Suppose I had started with 35 area codes. How should I have built the tree? What would happen to the efficiency of the program? What is the maximum possible number of trials necessary to find a node in that tree? What other numbers of nodes allow for perfect balance?
There are two important ideas to take away from this example. The first is that the choice of data representation can have a substantial effect on the efficiency of a program. The second, as I mentioned at the beginning of this section, is that we have used the same kind of data structure, a tree, for two very different purposes: first to represent a hierarchy (Sudbury is part of Massachusetts) and then to represent an ordering (313 is before 608).
An abstract data type, such as the tree type we've been discussing, must be implemented using some lower-level means for data aggregation, that is, for grouping separate things into a combined whole. In Berkeley Logo, there are two main built-in means for aggregation: lists and arrays. (Every dialect of Logo has lists, but not all have arrays.) Words can be thought of as a third data aggregate, in which the grouped elements are letters, digits, and punctuation characters, but we don't ordinarily use words as the basis for abstract data types.
Logo was designed to be used primarily by people whose main interest is in something other than computer programming, and so a design goal was to keep to a minimum the extent to which the Logo programmer must know about how Logo itself works internally. Even in these books, which are focused on computing itself, we've gotten this far without looking very deeply into how Logo's data structures actually work. But for the purposes of this chapter it will be useful to take that step.
Essentially all computers today are divided into a processor
and a memory. (The exceptions are experimental "parallel
processing" machines in which many small sub-processors and sub-memories
are interconnected, sometimes combining both capabilities within a single
intergrated circuit.) Roughly speaking, the processor contains the
circuitry that implements hardware primitive procedures such as arithmetic
operations. (Not every Logo primitive is a hardware primitive.) The
memory holds the information used in carrying out a program, including
the program itself and whatever data it uses. The memory is divided into
millions of small pieces, each of which can hold a single value (a number,
a letter, and so on).* Each small piece has an
address, which is a number used to select a particular piece;
the metaphor is the street address of each house on a long street. The
hardware primitive procedures include a load operation that takes
a memory address as its input and finds the value in the specified piece
of memory, and a store command that takes an address and a value
as inputs and puts the given value into the chosen piece of memory.
*I'm being vague about what a "value" is, and in fact most computer memories can be divided into pieces of different sizes. In most current computers, a byte is a piece that can hold any of 256 different values, while a word is a piece that can hold any of about four billion different values. But these details aren't important for my present purposes, and I'm going to ignore them. I'll talk as if memories were simply word-addressable.
With this background we can understand how lists and arrays differ. To be specific, suppose that we have a collection of five numbers to store in memory. If we use an array, that means that Logo finds five consecutive pieces of memory to hold the five values, like this:
If instead we use a list, Logo finds the memory for each of the five values as that value is computed. The five memory slots might not be consecutive, so each memory slot must contain not only the desired value but also a pointer to the next slot. That is, each slot must contain an additional number, the address of the next slot. (What I'm calling a "slot" must therefore be big enough to hold two numbers, and in fact Logo uses what we call a pair for each, essentially an array of length two.) Since we don't care about the actual numeric values of the addresses, but only about the pairs to which they point, we generally use arrows to represent pointers pictorially:
The last pair of the list has a null pointer, a special value to indicate that there is no next pair following it, indicated by the diagonal line.
Why do we bother to provide two aggregation mechanisms? Why don't language designers just pick the best one? Clearly the answer will be that each is "the best" for different purposes. In the following paragraphs I'll compare several characteristics of lists and arrays.
One advantage of arrays that should be obvious from these pictures is that a list uses twice as much memory to hold the same number of values. But this is not generally an important difference for modern computers; unless your problem is really enormous, you don't have to worry about running out of memory.
The most important advantage of arrays is that they are
random access. This means that each member of an array
can be found just as quickly as any other member, regardless of its
position within the array. If the program knows the address at which
the array begins, and it wants to find the nth member of the array,
only two operations are needed: First add n to the array's address,
then load the value from the resulting address. This takes a
constant (and very short) amount of time, O(1). By contrast, in a list
there is no simple arithmetic relationship between the address of the list's
first member and the address of its nth member. To find the nth member,
the program must load the pointer from the first pair, then use that
address to load the pointer from the second pair, and so on, n times.
The number of operations needed is O(n).
On the other hand, the most important advantage of lists is dynamic allocation. This means that the programmer does not have to decide ahead of time on how big the data aggregate will become. (We saw an example recently when we wanted to add a child to a node of an existing tree.) Consider the five-member aggregates shown earlier, and suppose we want to add a sixth member. If we've used a list, we can say, for example,
make "newlist fput "A :oldlist
and all Logo has to do is find one new pair:
By contrast, once an array has been created we can't expand it, because the new address would have to be adjacent to the old addresses, and that piece of memory might already be used for something else. To make an array bigger, you have to allocate a complete new array and copy the old values into it.
Remember that arrays sacrifice efficient expansion in order to get
efficient random access. From the standpoint of program speed, one is not
absolutely better than the other; it depends on the nature of the problem
you're trying to solve. That's why it's best if a language offers both
structures, as Berkeley Logo does. For the very common
case of foreach-like iteration through an aggregate, neither random
access nor dynamic allocation is really necessary. For a data base that can
grow during the running of a program, the flexibility of dynamic allocation
is valuable. For many sorting algorithms, on the other hand, it's important
to be able to jump around in the aggregate and so random access is useful.
(A programmer using arrays can partially overcome the lack of dynamic
allocation by preallocating a too-large array and leaving some of it empty
at first. But if the order of members in the array matters, it may turn out
that the "holes" in the array aren't where they're needed, and so the
program still has to copy blocks of members to make room. Also, such
programs have occasional embarrassing failures because what the programmer
thought was an extravagantly large array turns out not quite large enough
for some special use of the program, or because a malicious user deliberately
"overruns" the length of the array in order to evade a program restriction.)
The solitaire program in Volume 2 of this series illustrates the different advantages of lists and arrays. As in any card game, a solitaire player distributes the cards into several small groups, each of which varies in size as the play continues. For example, a typical step is to deal a card from the hand onto the pile, each of which is represented as a list:
make "pile fput (first :hand) :pile make "hand butfirst :hand
(The actual solitaire program uses somewhat different
instructions to accomplish the same effect, with a deal procedure that
outputs the next available card after removing it from the hand.)
On the other hand (no pun intended), shuffling the deck is easier when an array is used to hold the card values, because the shuffling algorithm requires random jumping around in the deck, but does not change the total number of cards, so that random access is more important than dynamic allocation. Therefore, the program starts each round of play with the deck in the form of an array of 52 cards. It shuffles the deck in array form, and then copies the members of the array into a list, which is used for the rest of that round. The advantage of an array for shuffling, and the advantage of a list for dealing cards, together outweigh the time spent copying the array into the list.
An important consequence of dynamic allocation is that lists are
sharable data structures. In the example above,
:oldlist contains five pairs and :newlist contains six, but the
total number of pairs used is six, not 11, because most of the same pairs
are part of both lists. That's why the fput operation takes O(1)
time, unaffected by the length of the list, as do first and
butfirst. (Now that you know how lists are constructed using pairs
and pointers, you should be able to understand something I've mentioned
earlier without explanation: Lput, last, and butlast
require O(n) time. It's much faster to operate near the beginning of a
list than near the end.) Arrays are not sharable; each array occupies its
own block of consecutive memory addresses.
When a data structure is both sharable and mutable, it's possible to get into some very mysterious, hard-to-detect bugs. Suppose we do this:
? make "one [Ice cream is delicious.] ? make "two fput "Spinach butfirst butfirst :one

Then suppose you decide you don't like spinach. You might say
? .setfirst butfirst butfirst :two "disgusting. ? print :two Spinach is disgusting.
But you haven't taken into account that :one and :two
share memory, so this instruction has an unintended result:
? print :one Ice cream is disgusting.
This is definitely a bug!
It's the combination of mutation and sharing that causes trouble. Arrays
are mutable but not sharable; the result of using setitem to change
a member of an array is easily predictable. The trouble with list mutation
is that you may change other lists besides the one you think you're changing.
That's why Berkeley Logo's .setfirst and .setbf primitives have
names starting with periods, the Logo convention for "experts only!" It's
also why many other Logo dialects don't allow list mutation at
all.*
*Also, this helps to explain the importance of property lists
in Logo. Property lists are a safe form of mutable list, because they are
not sharable; that's why the plist primitive outputs a newly-allocated
copy of the property list.In order to explain to you about how something like this might happen, I've had to tell you more about Logo's storage allocation techniques than is ordinarily taught. One of the design goals of Logo was that the programmer shouldn't have to think in terms of boxes and arrows as we're doing now. But if you mutate sharable lists, you'd better understand the boxes and arrows. It's not entirely obvious, you see, when two lists do share storage. Suppose the example had been backwards:
? make "one [Delicious, that's ice cream.] ? make "two lput "spinach. butlast butlast :one ? print :two Delicious, that's spinach. ? .setfirst :two "Disgusting, ? print :two Disgusting, that's spinach. ? print :one Delicious, that's ice cream.
In this case the other list is not mysteriously modified
because when lput is used, rather than fput as in the previous
example, the two lists do not share memory. That's a consequence of
the front-to-back direction of the arrows connecting the boxes; it's
possible to have two arrows pointing into a box, but only one arrow
can leave a box. You can't do this:

The combination of mutation and sharing, although tricky, is not all bad.
The same mutual dependence that made a mess of :one and :two in
the example above was desirable and helpful in the case of :world
and :Canada earlier. That's why Lisp has always included mutable
lists, and why versions of Logo intended for more expert users have also
chosen to allow list mutation.
Don't think that without mutable lists you are completely safe from mutual
dependence. Any language in which it's possible to give a datum a
name allows the programmer to set up the equivalent of sharable data,
just as I did in the final version of the tree of cities. As far as the
Logo interpreter is concerned, the value of the variable world is some
generated symbol like G47. That value is immune to changes in other
data structures. But if we think of :world as containing,
effectively, the entire tree whose root node is called G47, then
changes to other variables do, in effect, change the value of world.
What is true is that without mutable lists you can't easily set up a mutual
dependence by accident; you have to intend it.
By the way, by drawing the box and pointer diagrams with the actual data inside the boxes, I may have given you the impression that each member of a list or array must be a single number or letter, so that the value will fit in one memory address. Actually, each member can be a pointer to anything. For example, here's a picture of an array that includes lists,
{[A B C] D [E F]}
| (back to Table of Contents) | BACK chapter thread NEXT |
;;; Algorithms and Data Structures
;; Local optimization of quadratic formula
to quadratic :a :b :c
localmake "root sqrt (:b * :b-4 * :a * :c)
localmake "x1 (-:b+:root)/(2 * :a)
localmake "x2 (-:b-:root)/(2 * :a)
print (sentence [The solutions are] :x1 "and :x2)
end
;; Memoization of T function
to t :n :k
localmake "result gprop :n :k
if not emptyp :result [output :result]
make "result realt :n :k
pprop :n :k :result
output :result
end
to realt :n :k
if equalp :k 0 [output 1]
if equalp :n 0 [output 0]
output (t :n :k-1) + (t :n-1 :k)
end
;; Speedup of Simplex function
to simplex :buttons
output 2 * first (cascade :buttons
[fput (sumprods butfirst ?2 ?1) ?1] [1]
[fput 1 nextrow ?2] [1 1])
end
to sumprods :a :b
output reduce "sum (map "product :a :b)
end
to nextrow :combs
if emptyp butfirst :combs [output :combs]
output fput (sum first :combs first butfirst :combs) ~
nextrow butfirst :combs
end
;; Sorting -- selection sort
to ssort :list
if emptyp :list [output []]
output ssort1 (first :list) (butfirst :list) []
end
to ssort1 :min :in :out
if emptyp :in [output fput :min ssort :out]
if lessthanp :min (first :in) ~
[output ssort1 :min (butfirst :in) (fput first :in :out)]
output ssort1 (first :in) (butfirst :in) (fput :min :out)
end
;; Sorting -- partition sort
to psort :list
if emptyp :list [output []]
if emptyp butfirst :list [output :list]
localmake "split ((first :list) + (last :list)) / 2
if lessthanp first :list :split ~
[output psort1 :split (butfirst :list) (list first :list) []]
output psort1 :split (butlast :list) (list last :list) []
end
to psort1 :split :in :low :high
if emptyp :in [output sentence (psort :low) (psort :high)]
if lessthanp first :in :split ~
[output psort1 :split (butfirst :in) (fput first :in :low) :high]
output psort1 :split (butfirst :in) :low (fput first :in :high)
end
;; Sorting -- count comparisons
to lessthanp :a :b
if not namep "comparisons [make "comparisons 0]
make "comparisons :comparisons+1
output :a < :b
end
to howmany
print :comparisons
ern "comparisons
end
;; Abstract Data Type for Trees: Constructor
to tree :datum :children
output fput :datum :children
end
;; Tree ADT: Selectors
to datum :node
output first :node
end
to children :node
output butfirst :node
end
;; Tree ADT: Mutator
to addchild :tree :child
.setbf :tree (fput :child butfirst :tree)
end
;; Tree ADT: other procedures
to leaf :datum
output tree :datum []
end
to leaves :leaves
output map [leaf ?] :leaves
end
to leafp :node
output emptyp children :node
end
;; The World tree
to worldtree
make "world ~
tree "world ~
(list (tree "France leaves [Paris Dijon Avignon])
(tree "China leaves [Beijing Shanghai Guangzhou Suzhou])
(tree [United States]
(list (tree [New York]
leaves [[New York] Albany Rochester
Armonk] )
(tree "Massachusetts
leaves [Boston Cambridge Sudbury
Maynard] )
(tree "California
leaves [[San Francisco] Berkeley
[Palo Alto] Pasadena] )
(tree "Washington
leaves [Seattle Olympia] ) ) )
(tree "Canada
(list (tree "Ontario
leaves [Toronto Ottawa Windsor] )
(tree "Quebec
leaves [Montreal Quebec Lachine] )
(tree "Manitoba leaves [Winnipeg]) ) ) )
end
to locate :city
output locate1 :city :world "false
end
to locate1 :city :subtree :wanttree
if and :wanttree (equalp :city datum :subtree) [output :subtree]
if leafp :subtree ~
[ifelse equalp :city datum :subtree
[output (list :city)]
[output []]]
localmake "lower locate.in.forest :city (children :subtree) :wanttree
if emptyp :lower [output []]
output ifelse :wanttree [:lower] [fput (datum :subtree) :lower]
end
to locate.in.forest :city :forest :wanttree
if emptyp :forest [output []]
localmake "child locate1 :city first :forest :wanttree
if not emptyp :child [output :child]
output locate.in.forest :city butfirst :forest :wanttree
end
to cities :name
output cities1 (finddatum :name :world)
end
to cities1 :subtree
if leafp :subtree [output (list datum :subtree)]
output map.se [cities1 ?] children :subtree
end
to finddatum :datum :tree
output locate1 :name :tree "true
end
;; Area code/city pairs ADT
to areacode :pair
output first :pair
end
to city :pair
output butfirst :pair
end
;; Area code linear search
make "codelist [[202 Washington] [206 Seattle] [212 New York]
[213 Los Angeles] [215 Philadelphia] [303 Denver]
[305 Miami] [313 Detroit] [314 St. Louis]
[401 Providence] [404 Atlanta] [408 Sunnyvale]
[414 Milwaukee] [415 San Francisco] [504 New Orleans]
[608 Madison] [612 St. Paul] [613 Kingston]
[614 Columbus] [615 Nashville] [617 Boston]
[702 Las Vegas] [704 Charlotte]
[712 Sioux City] [714 Anaheim] [716 Rochester]
[717 Scranton] [801 Salt Lake City] [804 Newport News]
[805 Ventura] [808 Honolulu]]
to listcity :code
output city find [equalp :code areacode ?] :codelist
end
;; Area code binary tree search
to balance :list
if emptyp :list [output []]
if emptyp butfirst :list [output leaf first :list]
output balance1 (int (count :list)/2) :list []
end
to balance1 :count :in :out
if equalp :count 0 ~
[output tree (first :in) (list balance reverse :out
balance butfirst :in)]
output balance1 (:count-1) (butfirst :in) (fput first :in :out)
end
to treecity :code
output city treecity1 :code :codetree
end
to treecity1 :code :tree
if emptyp :tree [output [0 no city]]
localmake "datum datum :tree
if :code = areacode :datum [output :datum]
if :code < areacode :datum [output treecity1 :code lowbranch :tree]
output treecity1 :code highbranch :tree
end
to lowbranch :tree
if leafp :tree [output []]
output first children :tree
end
to highbranch :tree
if leafp :tree [output []]
output last children :tree
end
Brian Harvey,
bh@cs.berkeley.edu