Splitting Tori, Knots, and Moebius Bands
Carlo H. Séquin
Computer Science Division, EECS Department
Introduction
The inspiration for this study originated from the participation of Keizo Ushio [See Keizo Ushio's website: -- http://www2.memenet.or.jp/~keizo/ (2005).] at Isama'99 [See ISAMA 99, Conf. of Intnl. Soc. of The Arts, Mathematics and Architecture, San Sebastian, Spain, June 1999.] in San Sebastian, Spain. At that conference, he carved an intriguing sculpture consisting of two intertwined loops from a single solid block of granite (Fig.1). He started out by carving a massive torus with a relatively small hole. He then split that torus into two parts with a cut that sliced around the whole ring, and while doing so, twisted through 360º (Fig.1a). This cut the torus into two identical linked loops, each having a twisting cross section in the form of a half-circle. Once the two pieces had been pried apart, the constellation was reconfigured to make a dramatic figure-8 shape composed of the two loops placed into a position where portions of their original toroidal surfaces became coincident over a significant stretch (Fig.1b).
This process inspired me to start my own investigation to find out in what other intriguing ways a torus could be split. A straight-forward extension of the above geometry readily led to sets of more than two mutually interlocking rings (Section 2) and to multi-loops (Section 3) and Moebius space configurations (Section 4). Subsequently, I experimented with the splitting of Moebius bands (Section 6) and twisted knots (Section 7), which eventually led to a design for a snow sculpture (Section 8). Most recently, I gave myself the challenge to see whether a torus could also be split into a configuration of Borromean rings (Section 5), and how the splitting of these 1-manifold loop structures could be extended to more complex branching graph structures (Section 9). These concepts are illustrated with models made on a rapid prototyping machine.
Interlocking Rings
While Keizo Ushio's sculpture had to be created in painstaking hard labor by drilling some hundred holes into the hard granite torus, conceptually this operation amounts to sweeping a "knife" once around the torus, and in doing so, letting it execute one full twist around the curved toroidal axis. This separates the torus into two identical parts which however remain interlocked. If the two radii of the torus are suitably chosen, then the two rings can be re-arranged so that the outer curvature of one fits snugly into the inner curvature of the toroidal swept loop. In this constellation, the two rings seem to form a new symbiotic structure. A model of this configuration (Fig.2a) can easily be made on a rapid-prototyping (RP) machine. These two rings were made in a single run on a Fused Deposition Modeling (FDM) machine [See Stratasys, FDM machine: -- http://www.stratasys.com/NA/ (2005).], depositing thin, 0.01" thick layers of ABS plastic. A tiny twisting gap was left in the part description of the torus, which was then filled in by the FDM machine with some scaffolding of filler material. This material, being differently colored and more brittle than the material that forms the actual part, can easily be removed with a scalpel after the two halves of the torus have been pried apart.

Interlocking congruent rings cut from a single toroid: (a) 2 loops representing Keizo's sculpture; (b) 3 loops cut from a similar torus; (c) 4 loops cut from a twisted square toroid.
It seemed only natural to ask whether the torus could also be split into three congruent parts and how these parts might be arranged. It was quite obvious, that the cutting "knife" now had to have the shape of a three-spoked star where three straight blades join together at angles of 120º at the points of the toroidal axis; and again this 3-blade knife would be rotated through 360º as it swept once around the toroid. The result can be seen in Figure 2b; this structure forms a puzzle that is very satisfying to manipulate and to play with. However, so far I have not found any good sculptural constellation that matches the dramatic harmony of "OUSHI ZOKEI 1999" (Fig.1b).
Similarly, if the cutting "knife" has four "spokes" (equivalent to two cuts at right angles), then four interlocking loops would result (Fig.2c). The above configuration makes it quite clear how this paradigm can be extended to more than four parts. N interlocking rings can be generated by a knife with N blades coming together at angles of 360º/N at the points of the toroidal axis. The partitioning into 4 and into 6 parts is particularly attractive. In the first case, the cross sections of the individual rings can be made square, which then leads to a torus also with a square cross section. In the second case, if the individual rings have cross sections equal to an equilateral triangle, then the assembled torus would have a hexagonal profile. The symmetry of the cross sections of the individual rings makes these puzzles particularly intriguing − and for some people quite challenging − to put back together again, since it is not immediately obvious what faces need to be joined against one another.
Multi-Loops
The torus can also be cut by twisting a single straight "knife" through angles other than 360º. Keizo Ushio has explored many possibilities in his early work. Figure 3 shows what happens when the cut is rotated through 180º, 360º, and 540º, respectively. The second option represents the case discussed above, which later lead to "OUSHI ZOKEI 1999." But for the other two twisting angles something new happens: the torus is no longer cut into two parts, but remains connected as a single strand that loops twice around the central hole, and while doing so executes either a single twist of 360º (Fig.3a) or three full twists (Fig.3c). Figure 4a shows the first case more schematically.

Split tori by Keizo Ushio: (a) 180º twist (1989), (a) 360º twist (1992), (a) 540º twist (1996).
Again we can generalize this cutting action by using a "knife" that has three or more blades joining on the toroidal axis, and which executes twists of various amounts as it is swept around the toroidal loop. Figure 4b and 4c show the results for a 3-blade knife executing twists of 120º and 240º, respectively. In both cases the result is a single connected strand looping around the central hole three times. If we use a 4-blade knife, we can generate a quadruple loop for twist amounts of ±90º or ±270º. But if we use ±180º of twist, then the torus is actually divided into two double loops (Fig.4d). These two loops, however, are tightly nested and, unlike the case of Figure 2a, cannot be separated and put into an interesting sculptural configuration. Of course, in all those cases, in order to make the individual branches quite visibly distinct, one should use a "thick knife" that produces sizeable gaps between the individual branches of the multi-loop.
In summary, if we use a knife with n blades and apply a total twist angle of t*360º/n, the cut line on the surface forms a (t,n)-torus link, and so do the solid parts after the cut has been executed. The solid parts form g connected components, where g is the greatest common divisor of (t,n), and each link component is a (t/g, n/g)-torus knot. When t and n are relatively prime, there is only a single connected component.

Moebius Space
When building maquettes of potential sculptures, and peering into the gaps of some of the split tori, I often found myself agreeing with Nat Friedman, who has repeatedly pointed out at these conferences that for some abstract geometrical sculptures the spaces where material is missing may be even more important visually than the actual material itself. Thus, in my sculpture "Moebius Space" (Fig.5a) presented at Bridges 2000 [See C. H. Séquin, "- To Build a Twisted Bridge -" BRIDGES Conf. Proc., Winfield KS, July 2000, pp 23-34.], I hollowed out this space more dramatically and enhanced its visual impact by giving it a shining, silvery, almost mirror-like surface, while the outer torus surface was left dark and more textured. I am convinced that the effect will be quite dramatic if this sculpture is ever realized at a larger-than-human scale. In his 2004 implementation of such a Moebius cut through a torus Keizo Ushio has also dramatically enhanced the visibility of this inner space by coloring it orange (Fig.5b). In both these sculptures the material cut out from the torus has the shape of a Moebius band (hence the name of my sculpture). Figure 5c shows what happens when this space is equivalent to a Moebius band with three half-twists (Séquin 2005).
Borromean Rings
We have seen that the torus can be split into many intertwined rings. In all the above situations, every pair of rings is mutually interlocked. Can we also find an elegant way by which a torus is cut into a set of three Borromean rings (Fig.6a), in which no two individual rings are actually linked?
Borromean rings: (a) basic configuration, (b) 3 playdough rings squashed into a toroidal configuration, (c) 3 suitably interlinked loops cut from a torus.
To get some insight into this problem, I modeled the three Borromean rings from colorful playdough, placing the three differently colored links into the three main coordinate planes. I then compressed the configuration parallel to the {1,1,1} axis, while at the same time enlarging the central hole along this axis, and massaged the result to become a roughly toroidal configuration (Fig.6b). Inspecting the result made it clear that this is no longer just a torus link configuration. The three colors form a regular 3-strand braid around the toroidal loop, and each strand has to squeeze between the other two strands at two opposite positions in the toroidal loop. The main question now becomes how to best administer suitable cuts to achieve the necessary braiding of the three strands, while creating a geometry that still allows the three rings to be separated and put at right angle with respect to one another.
In a first phase I examined the relative positions of the three strands in the toroidal loop and created corresponding cross-sectional cuts in the form of a "Y", a "V", or a "| |". Then adjacent cross sections were morphed into one another. This did indeed create a geometry that trisected the torus into three pieces that had the desired topological linkage and which could be placed into the desired orthogonal Borromean configuration (Fig.6c). In order to obtain unobstructed movements of the three pieces from their resting position in the torus to the desired orthogonal constellation, one must take into account the relative motions of the three parts and fine-tune the cutting surfaces to follow the swept surfaces generated by these motions.
Splitting Moebius Bands
We have seen above that if the cutting knife is rotated by the right amount when slicing the torus, then we get Moebius-like results. This entices us to explore what happens when we start with a more typical Moebius band and then split this ribbon lengthwise. Most readers probably have done the experiment to cut lengthwise a Moebius band made from a simple paper strip, and then were fascinated when they obtained a single loop of twice the size and with a 360º twist. Splitting a Moebius band also has a lot of potential for aesthetically pleasing geometrical sculptures. M.C. Escher has made an attractive rendering of a split Moebius loop (Fig.7a). I also have been fascinated by this shape and have built various realizations of it on our rapid prototyping machine (Fig.7b,c). It should be pointed out, that the Moebius band cannot only be split sideways, but could also be split into two thin layers (Fig.7d); this configuration is most suitable for a realization in metal. Such a sculpture is available from Conrad Valett in Germany [See Conrad Valett's website: Valett Design: -- http://www.valett.de/ (2005).].

Split Moebius bands: (a) sketch by M.C Escher, (b), (c) corresponding FDM models, and
(d) a different way to split a Moebius band.
The split Moebius band is another one of Keizo Ushio's signature shapes (Fig.8a). Over the last 15 years he has sculpted dozens of variations; a few of them also result from splitting triply twisted bands (Fig.8b).

Splitting Knots
Splitting a simple Moebius band produces a single connected component that can be unfolded into a loop of twice the length of the original band. However, when we split a Moebius band with three half-twists, as depicted in Figure 7, then we obtain a knotted configuration corresponding to a trefoil knot. In Section 4 we have seen that when the torus is cut with the right combinations of n and t, one obtains a single torus knot. The simplest such torus knot is again the trefoil knot. If the sweep along the knot curve does not use a circular cross section but rather forms a "band" with distinctly different "width" and "thickness" values, then two other degrees of freedom appear in this shape: twist and azimuth. Changing them can dramatically alter the look and feel of a sculpture. In particular, there are only some twist values that maintain the three-fold symmetry of the trefoil knot, and only very few choices will make the ribbon seem to curve smoothly and organically around each other. If we try to form a trefoil knot from a flat ribbon, we find that the tightest configuration forms a one-sided loop, but it does not maintain 3-fold symmetry. In order to obtain a 3-fold symmetrical shape, we may give the ribbon either zero twist (seen in a projection along the symmetry axis) or impose three half-twists, as depicted in Figure 9a. Now we can split this ribbon, by letting the knife follow the curving and twisting of the band. Because of the built-in one-sidedness, the cut will not result in two separate components, but will produce a more complicated knot formed by a half-ribbon with twice the original length. Figure 10 shows a more artistic version of this same topology.
Trefoil knot split into 2, 3 and 4 strands.
If we try to form a tight and compact trefoil knot from an n-sided prism, we find that for n=4 we can join the ends of the prismatic strand with almost no apparent twisting (Fig.9c). However, where one lobe transitions into the next one, the Frenet frame that defines the osculating plane at each curve point exhibits a 90º torsional twist. Thus when we follow one of the prism edges, we find that it will jog to an adjacent position as we travel once around the whole knot, and we only return to the starting point after four passes around the knot. Splitting the 4-sided prismatic strand into four square fibers will thus lead to a single knotted loop of four times the length of the original strand.
Figure 9b explores the result of splitting the original strand that forms the trefoil knot into three fibers. In this case I have chosen a hexagonal cross section for the individual fibers and have used a minimal twist of 120º in the original strand to force the three fibers to connect into a single fiber traveling three times around the whole trefoil knot. Inspection of Figure 9b reveals that we have lost the original 3-fold symmetry of the knot. Maintaining that symmetry would force us to chose a twist value that then results in a linked configuration of three separate trefoil knots.
Snow Sculpture
In 2005 the theme of a split knot was used in the design of the entry of Team Minnesota to the annual snow sculpting competition in Breckenridge, Colorado. The design started from "Infinite Duality" (Fig.10b). However, the 3-fold symmetry was abandoned in order to obtain a more dramatic looking sculpture and to make the best possible use of the given snow blocks, measuring 10ft x 10ft x 12ft tall. The three lobes were raised to different heights to make a more artistic sculpture, with the tallest lobe spanning the full 12-foot height of the block (Fig.11). The whole curve was represented with a cubic B-spline, and the 15 control points were carefully adjusted so that the swept profile would just touch all sides of the block.

Maquettes for a Snow Sculpture: "Knot Divided" (a), (b), and final result (c).
In the first two days of snow sculpting we carved a rough representation of a triply twisted Moebius band wound up into a trefoil knot resting on three of its lobes (Fig.11a). Then we carefully split the upward lobes lengthwise, giving the resulting strands a more dramatic, crescent-like cross section. Since the original ribbon has an odd number of half-twists and thus is single sided, the splitting operation will not actually divide the knot into two parts, but will just produce a single strand of twice the length of the original ribbon − hence the name of the sculpture: "Knot Divided." During the first three days of the competition, the weather was unseasonably warm, with a strong sun and temperatures climbing up into the 40º range. Our major concern was the structural stability of the large leaning arched lobes. To reduce the weight of the lobes, the cross section was lightly tapered down towards the top. For better support, we let the lower sections of the lobes touch each other, and we did not split the original band into two strands all the way down to the platform on which the sculpture rested. This compromise solution is hardly visible in the photos taken from a few feet away and does not affect the beauty of the final result (Fig.11c). Fortunately on the last day of the competition, the temperature dropped considerably, and our sculpture stood for several days.
For the mathematically inclined, this sculpture also presents an interesting puzzle. While the original ribbon forms the simplest possible knot, the 3-crossing trefoil knot, the final structure forms a much more complicated knot. Can you figure out its crossing number? So far nobody has come up yet with the right answer on their first guess.
Splitting Graphs
All the objects we have split so far have been topologically equivalent to a simple loop, even though this loop may have been twisted and even knotted. In this final section we briefly consider what may happen if we split branching structures. Now the starting configuration may form a more complicated graph, and we now attempt to split/double each edge of this graph. To reduce the bewildering number of possible graphs that can be produced in this process, we limit ourselves to pairwise connections of the new edges, so that the final graph simply consists of one or more loops. As an example, if we start with the edge graph of a tetrahedron, we may then end up with just 4 triangular loops, one for each face of the tetrahedron (Fig.12a). Alternatively, we may construct three loops of four edges, each forming a Hamiltonian cycle on this graph (Fig.12b). Finally we can even connect all 12 edges into a single cycle (Fig.12c), which now allows to make this into a sculpture that holds together without any additional supports or connectors.
A couple of sculptures by Bathsheba Grossman [See Bathsheba Grossman's website: -- http://www.bathsheba.com/ (2005).], such as "FourWays" (Fig.13a) and "Alterknot" (Fig.13b) explore similar ideas. However, "FourWays" does not really separate the different strands, so it does not clearly reflect this paradigm. "Alterknot" maintains 3-way junctions at the inner tetrahedral shell. When I tried to re-design this structure so as to get rid of any junctions, I first obtained four separate clover leaves, one each on every face of the tetrahedron. I then tried to connect them into a single loop by rotating the split links through 180º. However, I have not found a way to obtain just a single loop while maintaining the full symmetry of the oriented tetrahedron. The best I could do is to maintain C3-symmetry, i.e., making one face (and one corner) somewhat different from the other three. One of the single-loop path solutions is shown in Figure 13c.
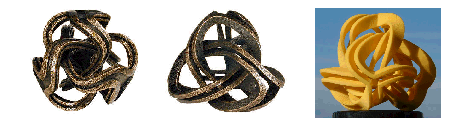
Conclusions
Many artists are fascinated by knots and tangles. Splitting the strands of such configurations lenghtwise is a simple structured way to obtain objects of the same kind but of higher complexity. Thus, in principle, the process could then be repeated. For sculptures that have to be created by manual labor, this recursion very quickly reaches a practical limit. On the other hand, objects designed procedurally on a computer can go much further, and the results may even be fabricated with a layered manufacturing technology.
I would like to thank Keizo Ushio for giving me permission to use his pictures of his work in this presentation. John Sullivan deserves credit for his constructive contributions and thorough review of the manuscript. I would like to express my gratitude to Stan Wagon, Dan Schwalbe, John Sullivan, and Richard Seeley for doing such a great job with the sculpting of "KNOT DIVIDED" and for providing a wonderful week of hospitality and friendship in Breckenridge, Colorado.
- Bathsheba Grossman's website: -- http://www.bathsheba.com/ (2005).
- ISAMA 99, Conf. of Intnl. Soc. of The Arts, Mathematics and Architecture, San Sebastian, Spain, June 1999.
- C. H. Séquin, "- To Build a Twisted Bridge -" BRIDGES Conf. Proc., Winfield KS, July 2000, pp 23-34.
- Stratasys, FDM machine: -- http://www.stratasys.com/NA/ (2005).
- Keizo Ushio's website: -- http://www2.memenet.or.jp/~keizo/ (2005).
- Conrad Valett's website: Valett Design: -- http://www.valett.de/ (2005).




