CS 39: Symmetry & Topology
Lecture #9 -- Mon. 4/8, 2019.

PREVIOUS <- - - - > CS 39R HOME < - - - - > CURRENT < - - - - > NEXT

Preparation:

"Correct" your Quiz (using a different color pen)
-- and catch up with your understanding of the course material.

Second try to make six small 3D objects that demonstrate these symmetries:
D1=C2; D2; S2; D1d=C2h; C1h=C1v; D1h=C2v.

Draw the Utility Graph and the Trefoil Knot onto a torus.

Warm-up:

Discuss your torus models with your neighbors.

Discuss your symmetry models with your neighbors.
Check whether your models have these properties:
D1=C2;    -- only one C2-axis.
D2;         -- two perpendicular C2-axes.
S2;            -- only one S2-axis.
D1d=C2h; -- one C2-axis + mirror plane perpendicular to it.
C1h=C1v; -- one single mirror plane.
D1h=C2v; -- two orthogonal mirror planes + a C2-axis at their intersection.

Chart of Cylinder Symmetries

Collect revised QUIZes.

Review some key concepts...

Mathematical Knots:

A wonderful, "must-have" resource: Colin C. Adams: "The Knot Book", W. H. Freeman and Co., New York, 1994.

Knot Tables
Simplifying knots: Reidemeister moves
Beautifying knots. . . -- Symmetry? Torus Knots
Beyond knots: Links! Link Tables

Applications in Nano Technology

The Beauty of Knots

Graph Theory:

Complete Graphs.
Bipartite Graphs. (Tripartite Graphs; Multi-partite Graphs...)
Planar Graphs.

How do Topology, Graph Theory, and Knot Theory relate to one another?
One important connection:
What is the handle-body of lowest genus on which a particular given graph or knot can be “embedded”, i.e., drawn without any crossings?
==>> Homework exercises: (1) Draw the Utility Graph onto a torus; (2) Draw the Trefoil Knot onto a torus.

Discuss Homework Results...

Smooth Topological Deformations: "Regular Homotopies"

From static shapes to dynamically deforming geometry:
(e.g., donut to coffee mug; models by H. Segerman, energy minimization):

Analyze which curves in 2D or surfaces in 3D are transformable into one another through a "Regular Homotopy",
i.e., a deformation that allows surface regions to pass through one another,
but does not allow any cuts, or tears, or formation of creases or other singular points with infinite curvature.
(With this definition, it is possible to turn a sphere or a torus inside out -- but it is not easy!).

Let's start with curves in 2 dimensions:

Try to accomplish the following curve-shape-changes in the plane
using a continuous smooth deformation ("regular homotopy").
Draw a sequence of smooth key-frame shapes that would make up a continuous movie.

Change this right-arm "Klein-bottle profile" into a left-arm "Klein-bottle profile".	Simplify this "double-8" curve as much as possible.	Try to turn a circle inside-out, (reversing arrow direction).

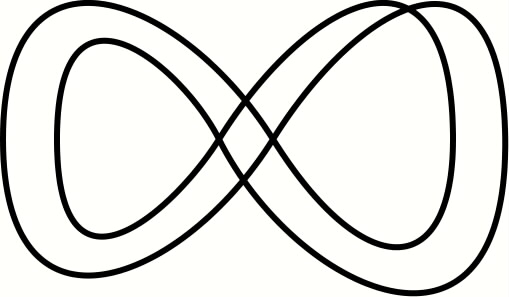
Solution Solution Solution
Remember: You are not allowed to ever make any sharp creases with very high curvature!

==> In the 2D plane, two smooth closed curves can be transformed into one another,
if the have the same "turning number"
(the number of full turns the headlights of a car would make while driving along the curve).

Derive the turning numbers of all the curves above...
Also, simplify the Klein-bottle profile as much as possible!

These movies show regular homotopies on surfaces in 3D space:

Torus eversion by Cheritat (cut open, to see inside);

Earliest approach to: Turning a sphere inside out by Nelson Max -- (in German!);

{ Turning a sphere outside in by Thurston } Details Levy, Maxwell, Munzner;

Energetically optimal sphere eversion by Sullivan, Francis, Levy.

A summary of the key steps in Morin's sphere eversion.

Snowsculpting ("Turning a Snowball Inside-Out").

Course Schedule and Project Presentations.