Spring Mass Systems:  Phase Space

Let's enhance our simple 1-particle system
by giving the particle some mass and reducing its damping.

Now, in addition to its location, we also need to specify the velocity of the particle to characterize its state completely.  This state can now be understood as a point in "Phase Space," which provides for every degree of freedom also a velocity for that component.
For our 1-dimensional, spring-suspended mass, the phase space is 2D and looks like this:

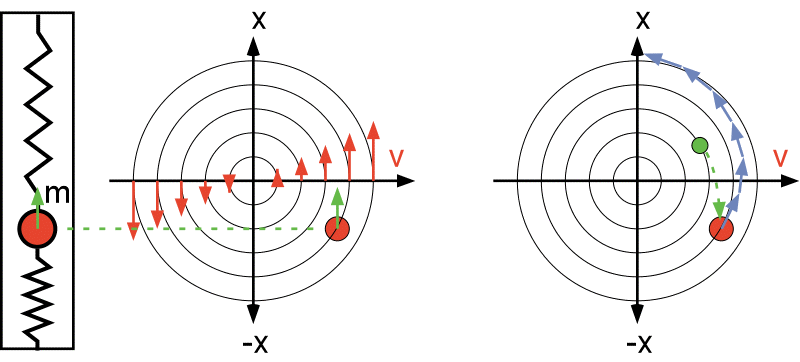
Again we must be careful to take really small time steps to keep our simulation reasonably accurate.
With the forward Euler method, no matter what we do, over time the system will gain energy
and the particle will spiral outward in Phase Space. 
This can be avoided if we introduce some damping in our system,
or if we use an  Implicit Method  to solve the ODE.

But Phase Space has another advantage:

It allows us to reduce a second order differential equation into coupled first-order ODE's:

x¨ = f(x, x˙, t) / m  ==>   x˙ = v   and   v˙ = f / m

Now a single particle moving in 3D physical space requires a 6D phase space for the description of its state;

and a spring-mass system with N particles in 3D will have a phase space with 6N dimensions!