Spring Mass Systems:  Euler's Method of Simulation

Let's try to simulate a very simple 1-particle system:

A mass-less particle suspended in viscous oil is held in the x=0 position by two springs;
these springs exert a restoring force equal to f = -kx.

If at some time t the particle is forced to position x and then released,
it will move in time towards x=0 along an exponential curve.
A dense sequence of such curves yields a vector-field that allows to read-off the motion
of any particle at a particular location at a particular time . . .

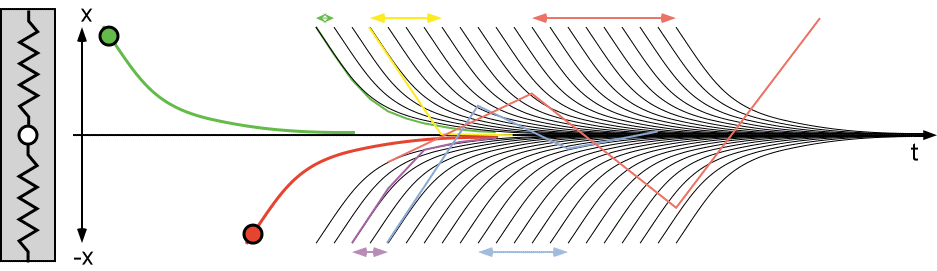
Now if we take finite-size time steps, the simulated behavior may change:
The green path follows the exponential curve reasonably well.
The purple path moves more quickly towards x=0.
The yellow path gets there in a single step.
The blue path overshoots and then oscillates for a while.
The red path gains amplitude with every time step . . .

If the system is stiff, i.e., if the constant k is large,
then the time steps will have to be rather small to yield a truthful simulation.
Fortunately there are better methods to solve differential equations:

To obtain better accuracy, we use more terms in the Taylor expansion of the functions in the vector field;
this leads to the Midpoint Method or to the higher-order Runge-Kutta methods.

To obtain better stability, we can use Implicit Methods, such as "backward" Euler;
they get their unconditional stability because they search for a real future state of the system,
which when used as the start of a backward simulation would then yield the current starting point.

Now let's introduce forces and accelerations . . .