Lab 2. Magnetic Measurements and Faraday's Law

NAME                                

Introduction.

Faraday's law (See RWVD Sec. 3.1-3.3 or SES Sec. 6.2) states that a voltage e(t) is induced at the terminals of a coil that "sees" a time-varying magnetic flux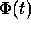

For an N turn coil, each turn having area A, the magnetic flux is 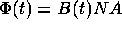, where B is the magnetic field. If the coil voltage e(t) is electronically integrated, then

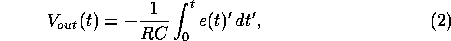
where RC is the time constant of the integrator. Combining (1) and (2), we obtain

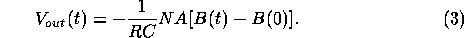
If B(0) = 0, then

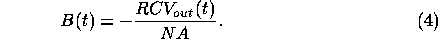
In this demonstration you will insert a coil into the static magnetic field of a solenoid (or turn on the magnetic field with the coil in place) and use (4) to determine the magnetic induction B(t) along the solenoid axis. You will compare to measurements made using a Bell 615 Gaussmeter.

Qualitative Observations:

1. Connect the 10 turn, large (3.5 cm) diameter coil to the Tektronix 549 storage oscilloscope. The scope settings and observing procedure are:
   1. Triggering Setting: A trigger mode = auto, Slope = +, Coupling = AC,
      Source = int. normal.
   2. Horizontal Display: Time base A at 0.1 sec/div or 0.2 sec/div.
   3. Erase Program: full, Auto Erase: off
   4. Observing Procedure:
      1. Push the "erase and reset" button.
      2. Swing the coil fast through the magnet within 1-2 sec.
      3. Observe the wave form on the oscilloscope.
      4. Do again if you want.
      5. Record the waveform you observe.

   

2. Swing the coil through the gap of the 0.3 tesla "magnetron" magnet to observe the induced voltage e(t). Sketch e(t) above, giving vertical and horizontal scales. Estimate the peak induced voltage that you expect to see: Expected peak voltage:        V.

Quantitative Measurements

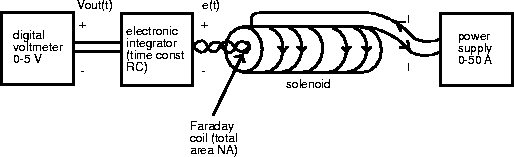
1. A schematic of the apparatus is shown above. Make sure that the solenoid current is off. Insert the multiturn Faraday measurement coil into the center of the solenoid (see previous figure). Connect the coil to the electronic integrator input. Connect the integrator output to the digital voltmeter, set to the 1 volt scale. Turn the integrator on and zero it. Adjust the potentiometer on the integrator to obtain the smallest drift in the voltage possible. Rezero the integrator when necessary. Then turn up the solenoid current to 10 amperes. Measure the voltage: 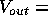        V. Using (3), find B using Faraday's law. You may rezero the integrator whenever necessary.
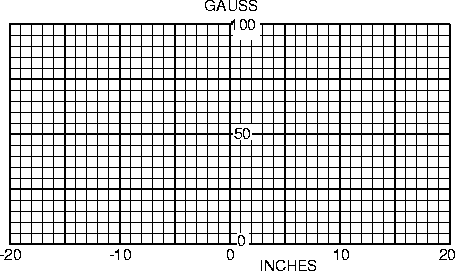
2. Using the Bell 615, Hall Effect Gaussmeter, measure the axial magnetic induction B(z) in the solenoid (every 2", including the center) for a solenoid current of 10 amperes. Compare the measured magnetic induction in the center of the solenoid to the measured value obtained from Faraday's law and to your calculated value using eq. (9) in Sec. 2.3 or eq. (7) in Sec. 2.4 of RWVD. Note: 1 gauss = 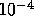tesla.

   

   Bell Gaussmeter measured        tesla
   Sec. 2.3 or 2.4 calculated        tesla
   Faraday's law measured        tesla

   Problem 2.3d of RWVD states that the magnetic induction at either end of a long solenoid should be approximately half that at its center. Explain why this should be the case: 
   
   What is B(center)/B(end) from your measurements? 

3. From your measurements, estimate the external inductance L of the solenoid using eq. (1) in Sec. 2.5 of RWVD (SES eq. 6.21): L=        mH.