Sparse learning via Boolean relaxations
Download: .pdf
Authors: Mert Pilanci, Martin J. Wainwright and Laurent El Ghaoui.
Status: Published in ·ath. Program., Ser. B (2015) 151:63–87.
Abstract: We introduce novel relaxations for cardinality-constrained learning prob- lems, including least-squares regression as a special but important case. Our approach is based on reformulating a cardinality-constrained problem exactly as a Boolean pro- gram, to which standard convex relaxations such as the Lasserre and Sherali-Adams hierarchies can be applied. We analyze the first-order relaxation in detail, deriving necessary and sufficient conditions for exactness in a unified manner. In the special case of least-squares regression, we show that these conditions are satisfied with high probability for random ensembles satisfying suitable incoherence conditions, similar to results on l1-relaxations. In contrast to known methods, our relaxations yield lower bounds on the objective, and it can be verified whether or not the relaxation is exact. If it is not, we show that randomization based on the relaxed solution offers a prin- cipled way to generate provably good feasible solutions. This property enables us to obtain high quality estimates even if incoherence conditions are not met, as might be expected in real datasets. We numerically illustrate the performance of the relaxation-randomization strategy in both synthetic and real high-dimensional datasets, revealing substantial improvements relative to
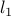-based methods and greedy selection heuristics.
Bibtex reference:
@article{PWE:15,
Author = {Mert Pilanci and Martin J. Wainwright and Laurent {El Ghaoui}},
Journal = {Math. Prog.},
Title = {Sparse learning via {B}oolean relaxations},
Year = {2015},
Month = may
}