Parameter Estimation with Expected and Residual-at-Risk Criteria
Download: .pdf
Authors: G. Calafiore, U. Topcu, L. El Ghaoui.
Status: Systems and Control Letters, 58 (1), p.39-46, Jan 2009.
Abstract: In this paper we study a class of uncertain linear estimation problems in which the data are affected by random uncertainty. We consider two estimation criteria, one based on minimization of the expected
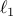 or
or 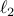 norm residual and one based on minimization of the level within which the
norm residual and one based on minimization of the level within which the 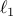 or
or 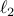 norm residual is guaranteed to lie
with an a-priori fixed probability (residual at risk). The random uncertainty affecting the data is characterized by means of its first two statistical moments, and the above criteria are intended in a worst-case probabilistic sense, that is worst-case expectations and probabilities over all possible distribution having the specified moments are considered.
The ensuing estimation problems can be solved efficiently via convex programming, yielding exact solutions in the
norm residual is guaranteed to lie
with an a-priori fixed probability (residual at risk). The random uncertainty affecting the data is characterized by means of its first two statistical moments, and the above criteria are intended in a worst-case probabilistic sense, that is worst-case expectations and probabilities over all possible distribution having the specified moments are considered.
The ensuing estimation problems can be solved efficiently via convex programming, yielding exact solutions in the 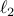 norm case and upper-bounds on the optimal solutions in the
norm case and upper-bounds on the optimal solutions in the 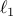 case.
case.
Bibtex reference:
@article{CET:09,
Author = {G. Calafiore and L. {El Ghaoui} and U. Topcu},
Journal = {Systems and Control Letters},
Title = {Parameter Estimation with Expected and Residual-at-Risk Criteria},
Volume = {58},
Number = {1},
Pages = {39--46},
Year = {2009}}