[ 2 -1 ]
[ -1 2 -1 ]
T(i) = 4^(-i) * [ -1 2 -1 ]
[ ... ... ... ]
[ -1 2 -1 ]
[ -1 2 ]
Weighted Jacobi is defined as
improved x(i)(j) = (1/3)*( x(i)(j-1) + x(i)(j) + x(i)(j+1) + b(i)(j) )One can confirm that one step of weighted Jacobi can also be written
improved x(i) = x(i) - (1/3)* 4^i * ( T(i)*x(i) - b(i) )The exact solution, xtrue(i), satisfies
xtrue(i) = xtrue(i) - (1/3)* 4^i * ( T(i)*xtrue(i) - b(i) )Subtracting these equations, and letting error(i) = x(i)-xtrue(i), yields,
improved error(i) = (I - (1/3)* 4^i * T(i)) * error(i)In other words, the error vector error(i) is multiplied by the matrix I-(1/3)*4^i*T(i) at each step. Recalling that we can write error(i) as a linear combination of eigenvectors v(j) of T(i)
error(i) = sum_{j=1} beta(j) * v(j)
let us see what happens to component beta(j) * v(j) of the error
after multiplying it by I-(1/3)*4^i*T(i).
Since v(j) is an eigenvector of T(i), we have
T(i) * v(j) = lambda(j) * v(j) where lambda(j) = 4^(-i)*2*(1-cos(j*pi/(2^i)))
Thus
(I - (1/3)*4^i*T(i)) * v(j) = (1 - (1/3)*4^i*lambda(j)) * v(j)
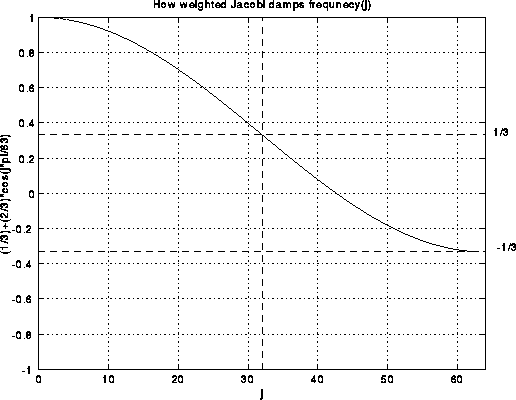
= ( (1/3) + (2/3)*cos(j*pi/2^i)) )* v(j)
If we plot the coefficient (1/3) + (2/3)*cos(j*pi/2^i)) versus j, we get
the following:

Thus, the upper half of the frequencies (demarcated by the dotted lines) are multiplied by a number between -1/3 and 1/3. This means weighted Jacobi decrease the high frequency error by at least a factor of 3 at each step.