We will outline the contents of these libraries, and discuss the design of the basic linear equation solver in some detail. The major issues will include
We will use Matlab notation to express our algorithms below. Recall that
The 6 most basic problem of linear algebra are summarized below. For details, see any good text book in numerical linear algebra, such as "Matrix Computations" by Golub and Van Loan, or "Numerical Linear Algebra" by J. Demmel. Lectures 11, 12 and 13 describe how some of these problems arise in doing simulations of physical systems.
After a summary of general computational aspects of these problems, we will discuss solving problem 1, Ax=b, using Gaussian elimination.The most important determiner of which algorithm to use for these problems is whether the matrix A is dense or sparse. A dense matrix has all (or mostly) nonzero entries, without any special properties that would let one represent using many fewer than n^2 independent numbers. Sparse matrices either have lots of zero entries, or are otherwise much more compactly representable than n^2 numbers. The algorithms for sparse matrices, which are very common in science and engineering, are often rather different than algorithms for dense matrices, and we will discuss them in detail in other lectures.
For a small example of a sparse matrix, click here. The first picture is a mesh around a wing. The physical problem is to compute the airflow around the wing at the mesh points. This leads to solving a sparse n-by-n system of spd linear equations Ax=b, where n=4253 and A has the "sparsity structure" in the top left plot of the second picture (black dots represent nonzero entries, the rest are zero). Only .16% of the 4253^2 entries of A are nonzero. The top right plot of the second picture is a different view of the matrix, with the rows and columns permuted. If we did Gaussian elimination on the spd matrix A without taking sparsity into account, it would take (1/3)*n^3 = 2.6e10 floating point operations. If we do Gaussian elimination on the matrix in the top left, and take sparsity into account by not doing unnecessary operations on zero entries, it does over 2200 times fewer operations, resulting in the Cholesky factor at the bottom left. If we do Gaussian elimination on the matrix at the top right, we get the Cholesky factor at the bottom right for 4 times fewer operations still. This matrix is available in matlab by typing demo, and clicking on
The next important distinction among linear algebra problems is between the first two problems (solving Ax=b and least squares problems), and the last problem (computing eigenvalues and the SVD). The first two problems have exact, finite solution procedures, and the latter can only be solved approximately. The first two problems have exact finite solutions in the sense that algorithms doing O(n^3) operations exist for each, which would yield the exact solution in the absence of round-off errors. (Analyzing roundoff is a topic for a numerical analysis class, and we will only mention it here when it requires us to modify the algorithm to make it reliable.) In contrast, to compute eigenvalues requires iterative solutions, because they implicitly require finding the roots of the characteristic polynomial of the matrix A: p(x)=determinant(A-x*I) (for the SVD substitute A'*A for A). As shown by Galois, no finite algorithm can exist to find the roots of a general polynomial of degree 5 or greater. A large variety of iterative solutions exist. In practice, the best iterations converge so reliably and so rapidly (quadratically, where the error is squared at every step, or even cubically) that they are often considered to be finite solutions.
Eigenvalue and singular value problems are all solved in 2 phases: a (finite) algorithm to reduce the original dense matrix to a more compactly representable form with the same eigenvalues (or singular values), and an iterative phase on the compact form. We will again distinguish the first two problems from the initial phases of the latter problems: For the first two problems, it is known how to do almost all the work by using matrix-matrix multiplication (BLAS3), which according to Lecture 2 is the fastest available linear algebra building block. In contrast, the first phases of the latter problems are more difficult to convert to BLAS3. The algorithm in LAPACK does 50% of its work in the BLAS3 and 50% in the slower matrix-vector multiplication (BLAS2). More recently, work on "multi-step band-reduction" by C. Bischof, X. Sun, and others has shown that if no eigenvectors are desired, one can use nearly 100% BLAS3. If eigenvectors are desired, one either has to use BLAS2 or increase the operation count significantly (by 2n^3).
In other words, we can in principle take nearly full advantage of the memory hierarchy for the first two problems, but not the latter ones, at least if eigenvectors are desired and we do not want to increase the operation count significantly.
Now consider just eigenvalue and singular value problems. The iterative phase of finding the eigenvalues of a general matrix is much more expensive than the initial reduction phase. In contrast, the best recent iterations for the symmetric eigenvalue problem and SVD are in principle much cheaper than the corresponding reduction phases (this was not true until recently).
Good parallel software for the first two problems exists in LAPACK and ScaLAPACK. Software for eigenvalue and singular value problems exists in LAPACK, with recent better algorithms on the way. ScaLAPACK currently only solves the symmetric eigenproblem, and the Feb 1995 release makes certain unfortunate compromises between parallel efficiency and accuracy, which future algorithms should make unnecessary. Class projects to improve and expand ScaLAPACK are available.
It is interesting to ask whether the best parallel algorithm is always a parallel version of the best serial algorithm. This is usually the case, and in fact the search for better parallel algorithms has sometimes led to better serial algorithms as well. However, there are some interesting exceptions. For example, certain "banded" linear systems can be solved more quickly using parallel-prefix than Gaussian elimination, but the results are numerically unstable in the presense of roundoff, and so potentially much less accurate. Currently, LAPACK and ScaLAPACK use different algorithms for finding eigenvalues, but we expect them to use the same algorithm eventually, once we better understand the problem.
... for each column i,
... zero it out below the diagonal by
... adding multiples of row i to later rows
for i = 1 to n-1
... each row j below row i
for j = i+1 to n
... add a multiple of row i to row j
for k = i to n
A(j,k) = A(j,k) -
(A(j,i)/A(i,i)) * A(i,k)

Let us improve this rudimentary implementation step by step. First, we remove the constant (A(j,i)/A(i,i)) from the innermost loop:
for i = 1 to n-1
for j = i+1 to n
m = A(j,i)/A(i,i)
for k = i to n
A(j,k) = A(j,k) - m * A(i,k)
Next, we avoid computing results we know, i.e. the zeros below the diagonal:
for i = 1 to n-1
for j = i+1 to n
m = A(j,i)/A(i,i)
for k = i+1 to n
A(j,k) = A(j,k) - m * A(i,k)
It will be convenient to store the multipliers m in the implicitly created
zeros below the diagonal, so we can use them later to transform the right
hand side b:
for i = 1 to n-1
for j = i+1 to n
A(j,i) = A(j,i)/A(i,i)
for j = i+1 to n
for k = i+1 to n
A(j,k) = A(j,k) - A(j,i) * A(i,k)
Now we use Matlab notation to express the algorithm even more compactly.
Note that the last two loops are really multiplying the column vector
A(i+1:n, i) times the row vector A(i, i+1:n), and add the resulting
(n-i)-by-(n-i) matrix to A(i+1:n, i+1:n):
for i = 1 to n-1
A(i+1:n, i) = A(i+1:n, i) / A(i,i)
A(i+1:n, i+1:n) = A(i+1:n, i+1:n) -
A(i+1:n, i)*A(i, i+1:n)
Thus, the inner loop consists of one BLAS1 operation (scaling
A(i+1:n,i) by a constant), and one BLAS2 operation (adding a rank-one matrix
-A(i+1:n,i)*A(i,i+1:n), to A(i+1:n, i+1:n)).
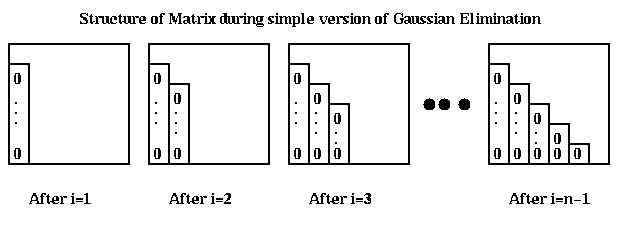
Here is a picture of what happens at step i.
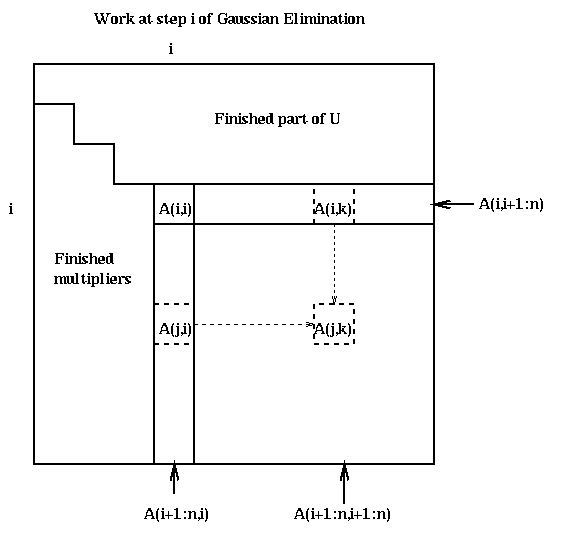
Call the strictly lower triangular matrix of multipliers which is stored below the diagonal of A after the algorithm ends M, and let L=I+M. Recall that U is the upper triangular matrix stored in the upper triangular of A. We state the following easy lemma without proof.
Lemma. (LU Factorization). If the above algorithm terminates (i.e. it did not try to divide by zero) then A = L*U.
Now we can state our complete algorithm for solving A*x=b:
1) Factorize A = L*U.
2) Solve L*y = b for y
by forward substitution.
3) Solve U*x = y for x
by backward substitution.
Then x is the solution we seek because A*x = L*(U*x) = L*y = b.
Let us compute the serial and PRAM complexity of this algorithm. From the matlab code, it is easy to see that the number of floating point operations performed (serial complexity) is
sum_{i=1}^{n-1}
[ (n-i)
... cost of A(i+1:n,i+1:n)/A(i,i),
+ 2*(n-i)^2 ]
... cost of A(i+1:n,i+1:n) -
... A(i+1:n,i)*A(i,i+1:n).
= (2/3)*n^3 + O(n^2)
Solving L*y=b and U*x=b each only cost n^2, so the total cost is
still (2/3)*n^3 + O(n^2).
Assuming we have one processor per matrix entry, and that communication is free (the PRAM model), the cost is
sum_{i=1}^{n-1}
[ 1
... cost of A(i+1:n,i+1:n)/A(i,i)
+ 2 ]
... cost of A(i+1:n,i+1:n) -
... A(i+1:n,i)*A(i,i+1:n)
= 3*(n-1)
since all the divisions in the inner loop can be done at once,
all the multiplications can be done at once, and all the subtractions
can be done at once. Thus, a lot of parallelism is available
in this algorithm for us to exploit. One can also confirm that solving
L*y=b and U*x = y in straightforward ways:
... in practice, y is overwritten on b
y(1:n) = b(1:n)
for i = 1 to n-1
y(i+1:n) = y(i+1:n) - y(i)*L(i+1:n,i)
... in practice, x is overwritten on y,
... i.e. on b
x(1:n) = y(1:n)
for i = n downto 1
x(i) = x(i)/U(i,i)
x(1:i-1) = x(1:i-1) - x(i)*U(1:i-1,i)
costs (1+2*(n-1)) + (1+n+2*(n-1)) = 5n-2, for a grand total of 8*n-5.
Interestingly, in the PRAM model, solving triangular systems with the
most straigthtforward algorithms is about as expensive as LU factorization,
whereas triangular system solving was much cheaper on a serial machine.
Here are some obvious problems with this algorithm, which we need to address:
A= [ 0 1 ]
[ 1 0 ]
then a warning is not deserved.
Even if A(i,i) is not exactly zero, but merely tiny, trouble is possible because of roundoff errors in floating point arithmetic. We illustrate with a 2-by-2 example. Suppose for simplicity we compute in 3-decimal digit arithmetic, so it is easy to see what happens. Let us solve Ax=b where
A= [ 1e-4 1 ] and b= [ 1 ] .
[ 1 1 ] [ 2 ]
The correct answer to 3 decimal places is easily confirmed to be
x = [ 1 ] .
[ 1 ]
The result of LU decomposition on A is as follows, where fl(a op b) is
the floating point result of a op b:
L = [ 1 0 ] = [ 1 0 ]
[ fl(1/1e-4) 1 ] [ 1e4 1 ]
... no error yet
and
U = [ 1e-4 1 ] = [ 1e-4 1 ]
[ 0 fl(1-1e4*1) ] [ 0 -1e4 ]
... error in the 4th place
The only rounding error committed is replacing 1-1e4*1 by -1e4, an error
in the fourth decimal place. Let's see how close L*U is to A:
L * U = [ 1e-4 1 ]
[ 1 0 ]
The (2,2) entry is completely wrong. If we continue to try to solve A*x=b,
the subsequent solves of L*y=b and U*x=y yield
y = [ 1 ] = [ 1 ]
[ fl(1-1e4*1) ] [ -1e4 ]
... error in the 4th place
and
x = [ x1 ] = [ fl((1-x2*1)/1e-4) ]
[ x2 ] [ fl(-1e4/(-1e4)) ]
= [ 0 ]
[ 1 ]
... no error in either component
We see that the computed answer is completely wrong, even though
there were only two floating errors in the 4th decimal place, and
even though the matrix A is "well-conditioned", i.e. changing the
entries of A or b by eps<<1 only changes the true solution by O(eps).
The problem can be traced to the first rounding error, U(2,2) = fl(1-1e4*1) = -1e4. Note that if we were to change A(2,2) from 1 to any other number z in the range from -5 to 5, we would get the same value of U(2,2) = fl(z-1e4*1) = -1e4, and so the final computed value of x would be the same, independent of z. In other words, the algorithm "forgets" the value of A(2,2), and so can't possibly get the right answer. This phenomenon is called numerical instability, and must be eliminated to yield a reliable algorithm.
The standard solution to this problem is called partial pivoting, which means reordering the rows of A so that A(i,i) is large at each step of the algorithm. In particular, at the beginning of step i of the algorithm, row i is swapped with row k>i if |A(k,i)| is the largest entry among |A(i:n,i)|. This yields the following algorithm.
Gaussian elimination with Partial Pivoting,
BLAS2 implementation
for i = 1 to n-1
find and record k where
|A(k,i)| = max_{i<=j<=n} |A(j,i)|
if |A(k,i)|=0, exit with a warning
that A is singular, or nearly so
if i != k, swap rows i and k of A
A(i+1:n, i) = A(i+1:n, i) / A(i,i)
... each quotient lies in [-1,1]
A(i+1:n, i+1:n) = A(i+1:n, i+1:n) -
A(i+1:n, i)*A(i, i+1:n)
If we apply this algorithm to our 2-by-2 example, we get a very accurate answer.
The LAPACK source for this routine, sgetf2, may be viewed by clicking here.
We may describe this algorithm as computing the factorization P*A=L*U, where L and U are lower and upper triangular as before, and P is a permutation matrix, i.e. the identity matrix with permuted columns. P*A is the matrix A with its rows permuted. As a consequence of pivoting, each entry of L has absolute value at most 1. Using this new factorization of A, solving A*x=b only requires the additional step of permuting b according to P.
Note that we have several choices as to when to swap rows i and k. Indeed, we could use indirect addressing and not swap them at all, but then we couldn't use the BLAS, so this would be slow. Different implementations make different choices about when to swap.
For LU decomposition, this means that we will process the matrix in blocks of b columns at a time, rather than one column at a time. b is called the block size. We will do a complete LU decomposition just of the b columns in the current block, essentially using the above BLAS2 code. Then we will update the remainder of the matrix doing b rank-one updates all at once, which turns out to be a single matrix-matrix multiplication, where the common matrix dimension is b. b will be chosen in a machine dependent way to maximize performance. A good value of b will have the following properties:
Gaussian elimination with Partial Pivoting,
BLAS3 implementation
... process matrix b columns at a time
for ib = 1 to n-1 step b
... point to end of block of b columns
end = min(ib+b-1,n)
... LU factorize A(ib:n,ib:end) with BLAS2
for i = ib to end
find and record k where
|A(k,i)| = max_{i<=j<=n} |A(j,i)|
if |A(k,i)|=0, exit with a warning
that A is singular, or nearly so
if i != k, swap rows i and k of A
A(i+1:n, i) = A(i+1:n, i) / A(i,i)
... only update columns i+1 to end
A(i+1:n, i+1:end) = A(i+1:n, i+1:end)
- A(i+1:n, i)*A(i, i+1:end)
endfor
... Let LL be the b-by-b lower triangular
... matrix whose subdiagonal entries are
... stored in A(ib:end,ib:end), and with
... 1s on the diagonal. Do delayed update
... of A(ib:end, end+1:n) by solving
... n-end triangular systems
... (A(ib:end, end+1:n) is pink below)
A(ib:end, end+1:n) =
LL \ A(ib:end, end+1:n)
... do delayed update of rest of matrix
... using matrix-matrix multiplication
... (A(end+1:n, end+1:n) is green below)
... (A(end+1:n, ib:end) is blue below)
A(end+1:n, end+1:n) = A(end+1:n, end+1:n)
- A(end+1:n,ib:end)*A(ib(end,end+1:n)
endfor
The LU factorization of A(ib:n,ib:end) uses the same algorithm as before. Solving a system of n-end equations with triangular coefficient matrix LL is a single call to a BLAS3 subroutine (strsm) designed for that purpose. No work or data motion is required to refer to LL; it is done with a pointer. When n>>b, almost all the work is done in the final line, which multiplies an (n-end)-by-b matrix times a b-by-(n-end) matrix in a single BLAS3 call (to sgemm). Here is a picture, where the final line subtracts the product of the blue and pink submatrices from the green submatrix.
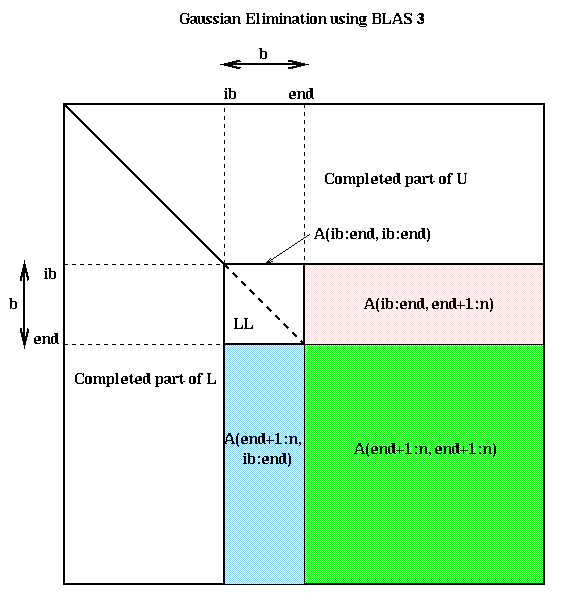
Here is another way to derive this algorithm. Suppose that we are at the top of the ib loop, midway through the algorithm. Then implicitly we have computed the following factorization, where all the submatrices are the same size as in the above figure (for simplicity we ignore pivoting):
ib-1 b n-b-ib
ib-1 [ A11 A12 A13 ]
b [ A21 A22 A23 ]
n-b-ib [ A31 A32 A33 ]
[ L11 0 0 ] [ U11 U12 U13 ]
= [ L21 I 0 ] * [ 0 A'22 A'23 ]
[ L31 0 I ] [ 0 A'32 A'33 ]
(all matrices are partitioned conformally).
Once we finish the i-loop, which LU factorizes A(ib:n,ib:end),
we have updated this factorization to
[ A11 A12 A13 ]
[ A21 A22 A23 ]
[ A31 A32 A33 ]
[ L11 0 0 ] [ U11 U12 U13 ]
= [ L21 I 0 ] * [ 0 L22*U22 A'23 ]
[ L31 0 I ] [ 0 L32*U22 A'33 ]
Following the triangular solve with LL,
we have further updated this factorization to
[ A11 A12 A13 ]
[ A21 A22 A23 ]
[ A31 A32 A33 ]
[ L11 0 0 ] [ U11 U12 U13 ]
= [ L21 I 0 ] * [ 0 L22*U22 L22*U23 ]
[ L31 0 I ] [ 0 L32*U22 A'33 ]
The final matrix multiply updates this to
[ A11 A12 A13 ]
[ A21 A22 A23 ]
[ A31 A32 A33 ]
[ L11 0 0 ]
= [ L21 L22 0 ]
[ L31 L32 I ]
[ U11 U12 U13 ]
* [ 0 U22 U23 ]
[ 0 0 A'33 - L32*U23 ]
[ L11 0 0 ] [ U11 U12 U13 ]
= [ L21 L22 0 ] * [ 0 U22 U23 ]
[ L31 L32 I ] [ 0 0 A''33 ]
At this point, we are done with the outer
loop, and have computed another b columns of L
and b rows of U. The algorithm continues by processing the next b
columns of A''33.
The LAPACK source for this routine, sgetrf, may be viewed by clicking here.
Now we fix the dimension at N=1000 and compare the efficiencies on a variety of architectures, from large vector processors like the Cray C90 and Convex C4640, to shared-memory multiple processor versions of both machines, to workstations like the DEC Alpha, IBM RS6000/590, and SGI Power Challenge. The vital statistics of these machines are given in the following table. All results are for 64-bit precision.
Machine #Procs Clock Peak Block
Speed Mflops Size b
(MHz)
---------------------------------------------
Convex C4640 1 135 810 64
Convex C4640 4 135 3240 64
Cray C90 1 240 952 128
Cray C90 16 240 15238 128
DEC Alpha 3000-500X 1 200 200 32
IBM RS 6000/590 1 66 264 64
SGI Power Challenge 1 75 300 64
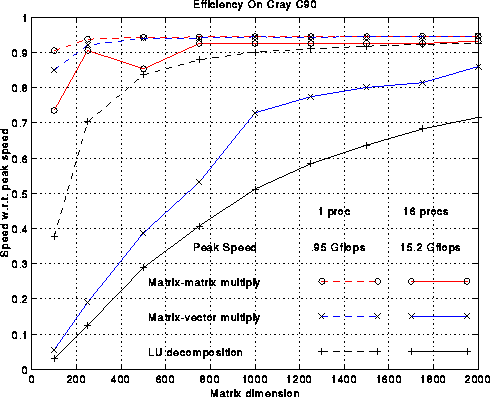
The figure below plots several efficiency measures for the
machines in the table.
There is one column in the plot for each machine.
First consider the green line, which measures the fraction of
peak performance attained by 1000-by-1000 matrix-multiplication.
We use the best matrix-multiplication available
for the machine, typically supplied by the vendor. For all machines
except the DEC Alpha 3000-500X, efficiency exceeds 90%.
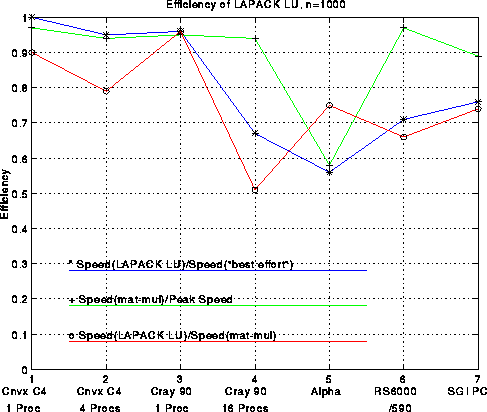
Now consider the red line, which is the speed of LU decomposition divided by the speed of matrix-multiply. The block size b is given in the above table; it was chosen by brute force search to optimize the performance. This curve measures how well we achieved our goal of making LU decomposition as fast as the matrix-multiply in its inner loop. The best efficiency, 95%, is attained on a single processor Cray C90, and the worst efficiency, 50%, is attained on a 16 processor Cray C90. This drop in performance is due to the fact that multiplying (n-i)-by-128 times 128-by-(n-i) matrices does not yield enough work to keep all 16 processors busy, although it is enough for 1 processor. The workstations (Alpha, RS6000, SGI) are all close to 70% efficient, which is reasonably satisfactory.
Finally, the blue line measures the efficiency of our LU decomposition with respect to "best effort", which means a version of LU decomposition crafted by each vendor especially for its machine. These vendor-supplied codes use very similar techniques to the ones described above, but try to improve performance by using a variable block size, assembly language, or an algorithm corresponding to a different permutation of the 3 nested loops in the original algorithm (all 3!=6 permutations lead to viable algorithms). The blue curve measures the extent to which we have sacrificed performance to gain portability: We have not lost much on the large vector machines, but 25%-30% on the workstations. The vendors typically invest a large amount of effort in optimizing 1000-by-1000 LU because it is one of the most popular benchmarks used to compare high performance machines: the LINPACK Benchmark. It would be nice if vendors had the resources to highly optimize all the library routines one might want to use, but few do, so portable high-performance libraries remain of great interest.
The LINPACK Benchmark is named after the predecessor of LAPACK. It originally consisted just of timings for 100-by-100 matrices, solved using a fixed Fortran program (sgefa) from the LINPACK linear algebra library. The data is an interesting historical record, with literally every machine for the last 2 decades listed in decreasing order of speed, from the largest supercomputers to a hand-held calculator. As machines grew faster and vendors continued to optimize their LINPACK benchmark performance (sometimes by using special compiler flags that worked only for the LINPACK benchmark!), the timings for 100-by-100 matrices grew less and less indicative of typical machine performance. Then 1000-by-1000 matrices were introduced. In contrast to the 100-by-100 case, which required vendors to use identical Fortran code, vendors were permitted to modify Gaussian elimination anyway they wanted for the 1000-by-1000 case, provided they got an accurate enough answer. Finally, a third benchmark was added for large parallel machines, which measured their speed on the largest linear system that would fit in memory, as well as the size of the system required to get half the Mflop rate of the largest matrix.
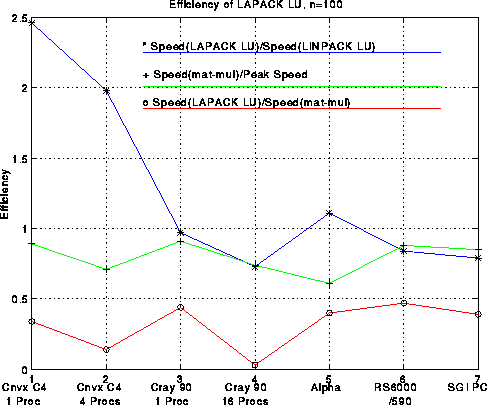
Here is a plot analogous to the last one but for 100-by-100 matrices. Generally speaking, efficiencies are lower for n=100 than n=1000, dramatically so for large machines like the Cray, less so for workstations. Rather than comparing LAPACK performance to the ``best effort'', it is compared to the LINPACK benchmark discussed above, i.e. performance using the LINPACK benchmark code sgefa. This ratio is as high as 2.46 for, but is as low as .73, a testimony to the efforts of the manufacturers to tune their compilers to work well on sgefa.
For an analysis and summary of the performance of other LAPACK routines besides LU, click here.
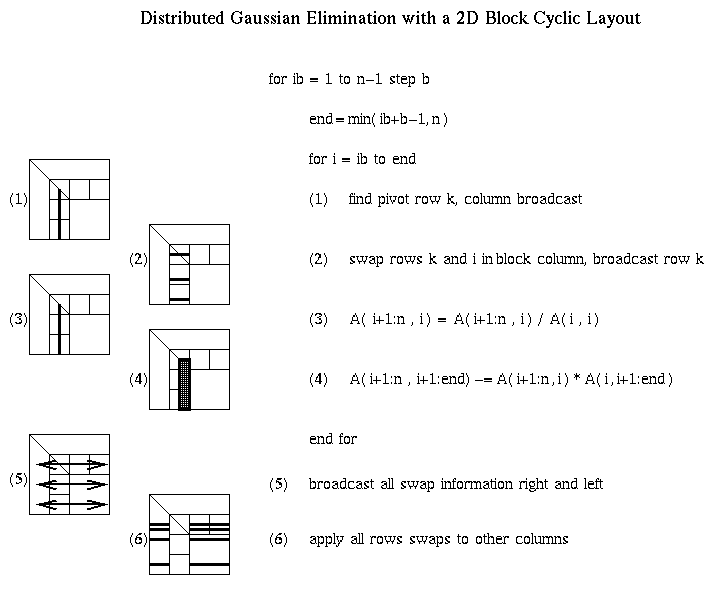
The two main issues in choosing a data layout for Gaussian elimination are

For convenience we will number the processors from 0 to p-1, and matrix columns (or rows) from 0 to n-1. The following figure shows a sequence of data layouts we will consider. In all cases, each submatrix is labeled with the number of the processor (from 0 to 3) that contains it. Processor 0 owns the shaded submatrices.

Consider the first layout, the Column Blocked Layout. In this layout, column i is stored on processor floor(i/c) where c=ceiling(n/p) is the maximum number of columns stored per processor. In the figure n=16 and p=4. This layout does not permit good load balancing, because as soon as the first c columns are complete, processor 0 is idle for the rest of the computation. The transpose of the this layout, the Row Blocked Layout, has a similar problem.
The second layout, the Column Cyclic Layout, tried to address this problem by assigning column i to processor i mod p. In the figure, n=16 and p=4. With this layout, each processor owns approximately 1/p-th of the square southeast corner of the matrix, so the load balance is good. However, the fact that single columns are stored rather than blocks means we cannot use the BLAS2 to factorize A(ib:n,ib:end), and may not be able to use the BLAS3 to update A(end+1:n,end+1:n). The transpose of this layout, the Row Cyclic Layout, has a similar problem.
The third layout, the Column Block Cyclic Layout, is a compromise between the last two. We choose a block size b, divide the columns into groups of size b, and distribute these groups in a cyclic manner. This means column i is stored in processor (floor(i/b)) mod p. In fact, this layout includes the first two as the special cases b=c=ceiling(n/p) and b=1, respectively. In the figure n=16, p=4 and b=2. For b larger than 1, this has a slightly worse balance than the Column Cyclic Layout, but can use the BLAS2 and BLAS3. For b less than c, it has a better load balance than the Columns Blocked Layout, but can only call the BLAS on smaller subproblems, and so perhaps take less advantage of the local memory hierarchy (recall our plot of performance of the BLAS3, where performance improved for larger matrix sizes). However, this layout has the disadvantage that the factorization of A(ib:n,ib:end) will take place on perhaps just on processor (in the natural situation where column blocks in the layout correspond to column blocks in Gaussian elimination). This would be a serial bottleneck.
This serial bottleneck is eased by the fourth layout in the figure, the Row and Column (or 2D) Block Cyclic Layout. Here we think of our p processors arranged in an prow-by-pcol rectangular array of processors, indexed in a 2D fashion by (pi,pj), 0 <= pi < prow and 0 <= pj < pcol. All the processors (i,j) with a fixed j are referred to as processor column j. All the processors (i,j) with a fixed i are referred to as processor row i. Matrix entry (i,j) is mapped to processor (pi,pj) by mapping i to pi and j to pj independently using the formula for a block cyclic layout:
pi = floor(i/brow) mod prow, where
brow = block size in the row direction
pj = floor(j/bcol) mod pcol, where
bcol = block size in the column direction
Thus, this layout includes all the previous layouts, and their transposes,
as special cases. In the figure, n=16, p=4, prow=pcol=2, and brow=bcol=2.
This layout permits pcol-fold parallelism in any column, and calls to the
BLAS2 and BLAS3 on matrices of size brow-by-bcol. This is the layout that
we will use for Gaussian elimination.
Since Gaussian elimination is not
entirely "symmetric" (there is more communication required during
the BLAS2 factorization of A(ib:n,ib:end) than during the BLAS3 update
of A(ib:end,end+1:n)), it is not clear that choosing an entirely
symmetric layout (prow=pcol) is most efficient. Indeed, later we will
see that choosing prow
For example, step (1) requires a reduction operation among the prow processors owning the current column, in order to find the largest absolute entry (pivot) and broadcast its index. Step (2) requires communication among processors in that column to exchange rows, and broadcast the pivot row to all processors in the column. Steps (3) and (4) are local computation, BLAS1 and BLAS2, respectively. Steps (5) and (6) involve communication, broadcasting pivot information and swapping rows among all the other p-prow processors. Step (7) is more communication, sending LL to all pcol processors in its row. Step (8) is local computation. Steps (9) and (10) are communication, sending matrix blocks right and down respectively, in preparation for the local matrix multiplies that update the trailing southeast square matrix in step (11).
It is unnecessary to have a barrier between each step of the algorithm. In other words, there can be parallelism with some steps of the algorithm forming a pipeline. For example, consider steps 9, 10 and 11, where most of the communication and floating point work occurs. As soon as a processor received its desired (blue) subblock of A(end+1:n,ib:end) from the left, and (pink) subblock of A(ib:end:end+1:n) from above, it may begin its local matrix multiply to update its part of the (green) submatrix A(end+1:n,end+1:n). As soon as the leftmost b columns of A(end+1:n,end+1:n) are updated, their LU factorization may begin while the remaining columns of the green submatrix are being updated by other processors.
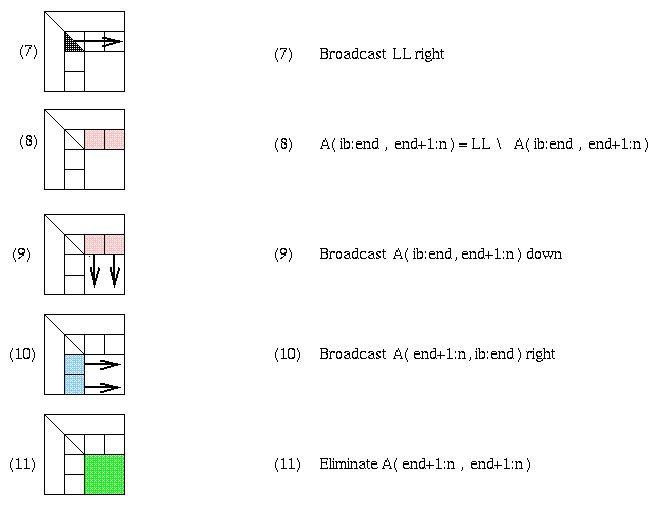
The ScaLAPACK software which implements this is located here. To view the top level routine that performs Gaussian elimination, pdgetrf.f, click here.
Time = msgs * alpha
+ words * beta + flops time units
where msgs is the number of messages sent
(not counting those sent in parallel), words is the number of words sent
(again not counting those sent in parallel), and flops is the number of
floating point operations performed (again, not counting those in parallel).
To make the presentation simple, we will only look at steps 9, 10 and 11 in
detail. It turns out these account for almost all of words and flops,
which are the most important terms for large n.
The implementation we discuss will overlap steps 10 and 11 of the algorithm as described above. More precisely,
Time for step 9 =
( log_2 prow ) *
( alpha + (b*(n-end)/pcol)*beta )
time units
( pcol ) *
( alpha + (b*(n-end)/prow)*beta )
time units.
However, since only the leftmost processor column in the green submatrix
needs to receive its message, pass it on, and update its submatrices,
before proceeding to LU factorize the next block column, we only charge
Time for step 10 =
2 * ( alpha + (b*(n-end)/prow)*beta )
time units.
Time for step 11 = 2*b*(n-end)^2/p
time units.
Time for all steps 9, 10 11 =
( ( n * (log_2 prow) + 2 ) / b )
* alpha
+ ( n^2 *
( (log_2 prow)/(2*pcol) + 1/prow )
) * beta
+ ( (2/3)*n^3/p )
Taking the other steps of algorithm into account increases the coefficients
of alpha and beta, yielding
Time for distributed Gaussian elimination =
( n * (6+ log_2 prow) ) * alpha
+ ( n^2 *
( 2*(prow-1)/p +
(pcol-1)/p +
(log_2 prow)/(2*pcol)
)
) * beta
+ ( (2/3)*n^3/p )
We compute the efficiency by dividing the serial time, (2/3)*n^3,
by p times the Time just displayed, yielding
Efficiency = 1 / ( 1
+ (1.5*p*(6 + log_2 prow)/n^2)
* alpha
+ ( 1.5*
( 2*prow + pcol
+ (prow * log_2 prow)/2 -3 )
/n )
* beta )
Let us examine this formula, and ask when it is likely to be close to 1,
i.e. when we can expect good efficiency. First, if communication were
free, so alpha=0 and beta=0, efficiency would be 1. This means we have
successfully balanced the load (modulo the lower order terms we are
ignoring).
Then, for fixed p, prow, pcol,
alpha and beta, the efficiency approaches 1 as n grows. This is because
we are doing O(n^3) floating point operations, but communicating only O(n^2)
words, so eventually the floating point, which is load balanced, swamps the
communication, so efficiency is good.
The efficiency also grows if alpha and beta shrink, i.e. as communication
becomes less expensive.
Now we consider the choice of prow and pcol. The expression
2*prow + pcol + (prow * log_2 prow)/2
= 2*prow +p/prow + (prow * log_2 prow)/2
is minimized when prow is slightly smaller than sqrt(p), meaning
we want a prow-by-pcol processor grid which is slightly longer than it
is tall. (In practice, for a given p, we are limited to choosing
prow and pcol among the factors of p, unless we want to have idle
processors.)
Overall, assuming prow ~ pcol ~ sqrt(p), and ignoring the log terms, the efficiency is
Efficiency = 1 / ( 1 + O( p/n^2 * alpha ) +
O( sqrt(p)/n * beta ) )
= E( n^2/p )
i.e. an increasing function of n^2/p. But n^2/p is the amount of
data stored per processor, since an n-by-n matrix takes up n^2 words.
In other words, if we let the "total problem size" n^2 grow proportionally
to the number of processor, we expect the efficiency to be approximately
constant. Let us confirm this hypothesis with an experiment.
We will use the Intel Gamma, which has the following machine parameters:
p prow pcol
--- ---- ----
1 1 1
16 4 4
32 4 8
64 8 8
128 8 16
Memory per processor will be taken as 8*n^2/p bytes = 2, 3, 4, 5 and 6.25
Megabytes.
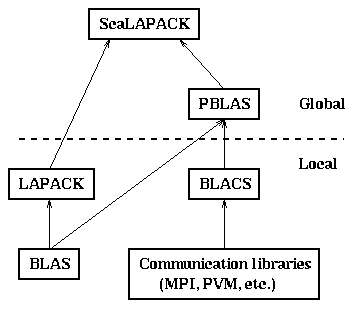
Below the dotted line is local software, and above the dotted line is global software. Local software either only runs on one processor, and is not parallel, or refers to other processors explicitly to do communication. Global software refers to data structures, and operations on them, that are spread out over the whole parallel machine (or selected subsets).
We have already discussed the BLAS, or Basic Linear Algebra Subroutines, at length in Lecture 2, and will not dwell on them here. The use of the BLAS, especially BLAS3, in LAPACK is discussed above. Neither the BLAS nor LAPACK are explicitly parallel.
(We note that on shared memory parallel machines, it is possible to hide all the parallelism within the BLAS, by doing matrix-matrix multiplication in parallel for example, and so to run LAPACK in parallel without changing any software. The extra complexities of ScaLAPACK are due to the lack of a shared address space. Also, there are some LAPACK routines for eigenvalue problems, whose ScaLAPACK counterparts use different algorithms. We discuss these in other lectures.)
The BLACS are the Basic Linear Algebra Communication Subroutines. These routines are message passing libraries which let the user send, receive, broadcast, reduce and do other basic operations on the matrix data types used in ScaLAPACK algorithms, namely rectangular or trapezoidal matrices, and submatrices of other matrices. The BLACS hide (almost all!) the differences between the underlying message passing libraries (PVM, MPI, MPL for the IBM SP-1 and SP-2, CMMD for the CM-5, and NX for the Intel Paragon). This permits the software using the BLACS to be the same across platforms. The design of the BLACS is discussed in detail in "A User's Guide to the BLACS v1.0," by J. Dongarra and R. C. Whaley, LAPACK Working Note 94, University of Tennessee Report CS-95-286, April 1995.
(There are two caveats to this claim. First, PVM requires a slightly different initialization sequence. Second, there are various tuning parameters to suggest how the BLACS can best use the underlying processor topology (ring, 2D-mesh, tree, etc.).)
The PBLAS are the Parallel BLAS. They implement BLAS operations on matrices distributed in a 2D block-cyclic fashion as described above.
Given all this infrastructure, the high level ScaLAPACK code for Gaussian elimination (pdgetrf.f) has essentially the same structure as the sequential LAPACK code (sgetrf.f). This is not just esthetically pleasing, but essential to be able to understand and maintain the large body of software comprising LAPACK, CLAPACK and SCLAPACK (currently between 2 and 3 million lines, some of it generated automatically from other parts).
In order to appreciate the complexity hidden by this layering, let us briefly examine how 2D block cyclic matrices are represented. internally in the PBLAS. If fact, let us recall how matrices are represented in Fortran on a single sequential machine. Matrices in Fortran are stored columnwise (not rowwise, as in C), which means that the leading dimensions change fastest as we traverse memory. So the simplest representation is
loc(B(i,j)) = loc(A(5,4)) + (i-1) + (j-1)*LDA
Yet more information is needed by the PBLAS to represent (an arbitrary submatrix) of a 2D block cyclic matrix spread out over an PROW-by-PCOL grid of processors. Indeed, each matrix has a 9-element descriptor containing
To refer to a submatrix of such a matrix, we separately need the indices I and J of its upper left corner A(I,J), the number of its rows, and the number of its columns.
For details on the design of the PBLAS, see