Routine Plot Function
Label
------- ----- --------
xGESV 1 Solve Ax=b using
Gaussian elimination
xGELS 2 Solve a least squares problem
xGEEEV(N) 3 Find the eigenvalues
of a general matrix
xGEEEV(V) 4 Find the eigenvalues and
eigenvectors of a
general matrix
xSYEVD(N) 5 Find the eigenvalues
of a symmetric matrix
xSYEVD(V) 6 Find the eigenvalues and
eigenvectors of a
symmetric matrix
xGESVD(N) 7 Find the singular values
of a general matrix
xGESVD(V) 8 Find the singular values and
singular vectors of a
general matrix
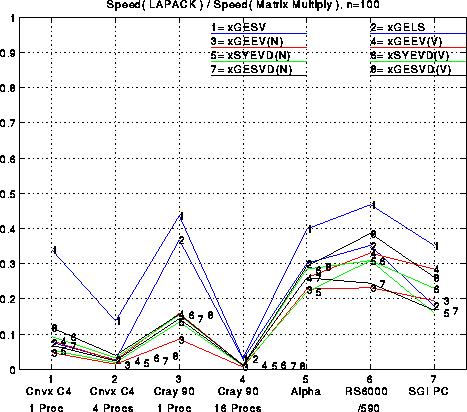
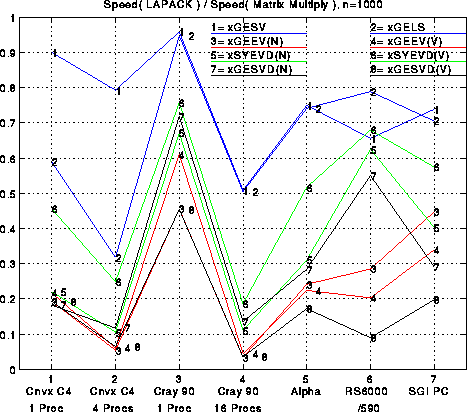
The rather busy figure below has several interesting features. First, solving linear systems (xGESV) is most efficient, closely followed (on all but the Convex) by solving a least squares problem (xGELS). Both algorithms use delayed updates to convert nearly all floating point operations to BLAS3. The updates used by xGELS are somewhat more complicated mathematically than for xGESV, and so require some algebraic manipulations to figure out how to delay them. (For details see "A Storage Efficient WY representation for products of Householder transformations" by R. Schreiber and C. Van Loan, SIAM J. Sci. Stat, Comput., 1989, pp 53--57.)
The next most efficient routines are for finding eigenvalues only (xSYEVD(N)) or eigenvalues and eigenvectors (xSYEVD(V)) of symmetric matrices. As we described before, there is a reduction phase and an iterative phase to this algorithm. The reduction phase is at best about 50% BLAS3 and 50% BLAS2, which reduces efficiency. If eigenvalues only are desired, the iterative phase is negligible. If eigenvectors are desired, however, the standard iterative phase algorithm, dating from the 1960s, uses only BLAS1 operations, so it is quite inefficient and takes much longer than the reduction phase. Only recently have we implemented a suitable replacement which is much more efficient, uses an entirely different algorithmic approach, and uses BLAS3 operations extensively. (For details of the implementation see "A serial implementation of Cuppen's divide and conquer algorithm for the symmetric eigenvalue problem", by J. Rutter, Berkeley MS Thesis in Mathematics, 1994.)
The algorithms available for the singular value decomposition (xGESVD(N) and xGESVD(V)) are very similar to those for the symmetric eigenvalue problem. Indeed, the graph shows that the efficiencies when eigenvalues only are desired (xSYEVD(N)), and when singular values only are desired (xGESVD(N)) are rather close. However, we have not yet completed the new algorithm for singular vectors analogous to the new routine for eigenvectors described above. Instead, we use the conventional BLAS1 algorithm, and the graph shows it has dramatically worse efficiency. We plan to release the new singular vector routine sometime in 1995.
Finally, we see that the routines for finding eigenvalues and eigenvectors of nonsymmetric matrices (xGEEV(N) and xGEEV(V)) are generally the least efficient routines of all. As with other eigenvalues algorithms, there is a reduction phase and an iterative phase. The reduction phase is at best 50% BLAS3. But the iterative phase is quite dominant, and so far no significant improvement on the traditional BLAS1 algorithm has emerged, though many have been tried and are still being explored.

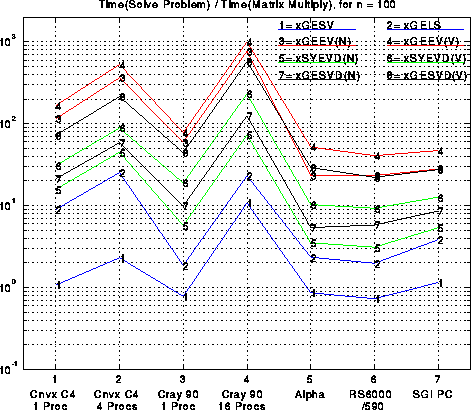
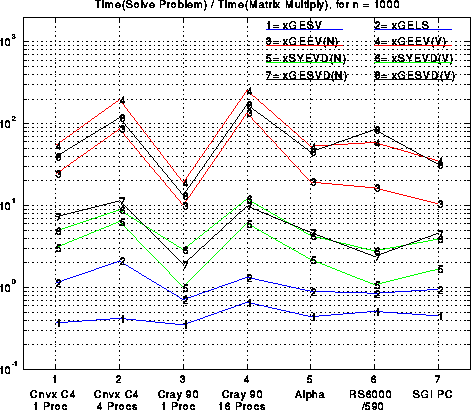
The efficiencies in the last plot do not indicate the relative expenses of these operations. Briefly, solving linear systems (xGESV) is the cheapest of the 8 operations shown, typically costing anywhere from 1/3 to 2/3 of a matrix multiply. Solving a least squares problem is a little slower. Next comes finding eigenvalues only of symmetric matrices, or singular values, costing anywhere from 1 to 10 matrix multiplies, depending on the machine. Eigenvectors of symmetric matrices are in the same range. Finally, finding eigenvalues and/or eigenvectors of nonsymmetric matrices is significantly more expensive, costing at least 10, and up to several hundred times as much as a matrix multiply. Computing singular vectors is comparably expensive, although as described above we expect significant improvements in the coming year. For more performance details, see the Chapter 3 of the LAPACK Manual.
The block sizes b were chosen by brute-force search: many values of b were tried and the best one chosen. A possible class project would involve more careful performance modelling to help choose the best b automatically.
For completeness, we include the same two plots just shown for n=100 instead of n=1000: efficiency of matrix multiply and LU, efficiency of 8 main LAPACK routines, and speed w.r.t. matrix multiplication. Generally speaking, efficiencies are lower for n=100 than n=1000, dramatically so for large machines like the Cray, less so for workstations.