Split-C was designed at Berkeley, and is intended for distributed memory multiprocessors. It is a small SPMD extension to C, and meant to support programming in data parallel, message passing and shared memory styles. Like C, Split-C is "close" to the machine, so understanding performance is relatively easy. Split-C is portable, and runs on the
The best document from which to learn Split-C is the tutorial Introduction to Split-C. There is a debugger available as well: Mantis.Extensions of Split-C to include features of multithreading (as introduced in Lecture 6) and C++ classes are under development, and will be released soon.
We begin with a general discussion of Split-C features, and then discuss the solution to Sharks & Fish problem 1 in detail. The most important features of Split-C are
int *Pl, *Pl1, *Pl2 /* local pointers */
int *global Pg, Pg1, Pg2 /* global pointers */
int *spread Ps, Ps1, Ps2 /* spread pointers */
The following assignment sends messages to fetch the data pointed to by
Pg1 and Pg2, brings them back, and stores their sum locally:
*Pl = *Pg1 + *Pg2
Execution does not continue until the entire operation is complete.
Note that the program on the processors owning the data pointed to by
Pg1 and Pg2 does not have to cooperate in this communication in any explicit
way. Thus, it is very much like a shared memory operation, although it
is implemented on distributed memory machines, in effect interrupting
the processors owning the remote data, getting the data and
sending it back to the requesting processor, and letting them continue.
In particular, there is no notion of needing matched sends and receives
as in a message passing programming style. Rather than calling this send or receive,
the operation performed is called a get, to emphasize that the
processor owning the data need not anticipate the request for data.
The following assignment stores data from local memory into a remote location:
*Pg = *Pl
As before, the processor owning the remote data need not anticipate the arrival
of the message containing the new value. This operation is called a
put.
Global pointers permit us to construct distributed data structures which span the whole machine. For example, the following is an example of a tree which spans processors. The nodes of this binary tree can reside on any processor, and traversing the tree in the usual fashion, following pointers to child nodes, works without change.
typedef struct global_tree *global gt_ptr
typedef struct global_tree{
int value;
gt_ptr left_child;
gt_ptr right_child;
} g_tree
We will discuss how to design good distributed data structures later
when we discuss the
Multipol
library.
Global pointers offer us the ability to write more complicated and flexible programs, but also get new kinds of bugs. The following code illustrates a race condition, where the answer depends on which processor executes "faster". Initially, processor 3 owns the data pointed to by global pointer i, and its value is 0:
Processor 1 Processor 2
*i = *i + 1 *i = *i + 2
barrier() barrier()
print 'i=', i
It is possible to print out i=1, i=2 or i=3, depending on the order in
which the 4 global accesses to i occur. For example, if
processor 1 gets *i (=0) processor 2 gets *i (=0) processor 1 puts *i (=0+1=1) processor 2 puts *i (=0+2=2)then the processor 1 will print "i=2". We will discuss programming styles and techniques that attempt to avoid this kind of bug.
A more interesting example of a potential race condition is in a job queue, a data structure for distributing chunks of work of unpredictable sizes to different processors. We will discuss this example below after we present more feature of Split-C.
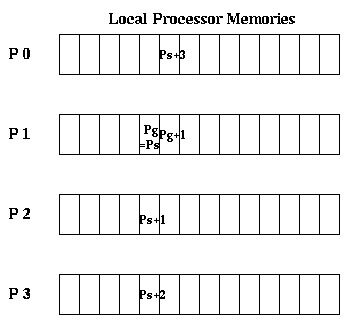
Global pointers may be incremented like local pointers: if Pg = (processor,offset), then Pg+1 = (processor,offset+1). This lets one index through a remote part of a data structure. Spread pointers differ from global pointers only in this respect: if Ps = (processor,offset), then
Ps+1 = (processor+1 ,offset) if processor < PROCS-1, or
= (0 ,offset+1) if processor = PROCS-1
where PROCS is the number of processors.
In other words, viewing the memory as a 2D array, with one
row per processor and one column per local memory location, incrementing
Pg moves the pointer across a row, and incrementing Ps moves the pointer
down a column. Incrementing Ps past the end of a column moves Ps to the
top of the next columns.

The local part of a global or spread pointer may be extracted using the function to_local.
Only local pointers may be used to point to procedures; neither global nor spread pointers may be used this way. There are also some mild restrictions on use of deferenced global and spread pointers; see the last section of the Split-C tutorial.
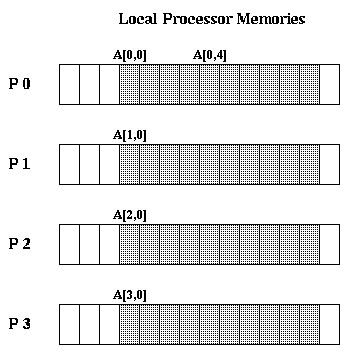
static int A[PROCS]::[10]
declares an array of 10 integers in each processor memory.
The double colon is called the spreader, and indicates that
subscripts to its left index across processors, and subscripts
to the right index within processors. So for example
A[i,j] is stored in location to_local(A)+j on processor i.
In other words, the 10 words on each processor reside at the
same local memory locations.
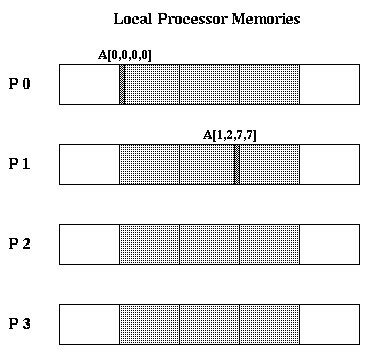
The declaration
static double A[PROCS][m]::[b][b]
declares a total of PROCS*m*b^2 double precision words. You may think of this as
PROCS*m groups of b^2 doubles being allocated to the processors
in round robin fashion. The memory per processor is
b^2*m double words. A[i][j][k][l] is stored in processor
i*m+j mod PROCS,
and at offset
to_local(A) + b^2*floor( (i*m+j)/PROCS ) + k*b+l
In the figure below, we illustrate the layout of A[4][3]::[8][8]
on 4 processors.
Each wide light-gray rectangle represents 8*8=64 double words. The two
wide dark-gray rectangles represent wasted space. The two thin
medium-gray rectangles are the very first word, A[0][0][0][0],
and A[1][2][7][7], respectively.
In addition to declaring static spread arrays, one can malloc them:
int *spread w = all_spread_malloc(10, sizeof(int))This is a synchronous, or blocking, subroutine call (like the first kind of send and receive we discussed in Lecture 6), so all processors must participate, and should do so at about the same time to avoid making processors wait idly, since all processors will wait until all processors have called it. The value returned in w is a pointer to the first word of the array on processor 0:
w = (0, local address of first word on processor 0).
(A nonblocking version, int *spread w = spread_malloc(10, sizeof(int)), executes on just one processor, but allocates the same space as before, on all processors. Some internal locking is needed to prevent allocating the same memory twice, or even deadlock. However, this only works on the CM-5 implementation and its use is discouraged.)
c := *global_pointer ... c is a local variable
... other work not involving c ...
synch()
b = b + c ... b is a local variable
initiates a get of the data pointed to by global_pointer, does other useful
work, and only waits for c's arrival when c is really needed,
by calling synch().
This is also called prefetching, and permits communication
(getting c) and computation to run in parallel.
The statement
*global_pointer := b
similarly launches a put of the local data b into the remote location
global_pointer, and immediately continues computing. One can also wait
until an acknowledgement is received from the processor receiving
b, by calling synch().
Being able to initiate a remote read (or get) and remote write (or put), go on to do other useful work while the network is busy delivering the message and returning any response, and only waiting for completion when necessary, offers several speedup opportunities.
Instead of synching on all outstanding puts and gets, it is possible to synch just on a selected subset of puts and gets, by associating a counter just with those puts and gets of interest. The counter is automatically incremented whenever a designated put or get is initiated, and automatically decremented when an acknowledgement is received, so one can test if all have been acknowledged by comparing the counter to zero. See section 10.5 of Introduction to Split-C for details.
The freedom afforded by split-phase assignment also offers the freedom for new kinds of bugs. The following examples illustrates a loss of sequential memory consistency. Sequential consistency means that the outcome of the parallel program is consistent with some interleaved sequential execution of the PROCS different sequential programs. For example, if there are two processors, where processor 1 executes instructions instr1.1, instr1.2, instr1.3, ... in that order, and processor 2 similarly executes instr2.1, instr2.2, instr2.3 ... in order, then the parallel program must be equivalent to executing both sets of instructions in some interleaved order such that instri.j is executed before instri.(j+1). The following are examples of consistent and inconsistent orderings:
Consistent Inconsistent
instr1.1 instr1.1
instr2.1 instr2.2 *out of order
instr1.2 instr1.2
instr2.2 instr2.1 *out of order
instr1.3 instr1.3
instr2.3 instr2.3
... ...
Sequential consistency, or having the machine
execute your instructions in the order you intended,
is obviously an important tool if you want to predict
what your program will do by looking at it.
Sequential consistency can be lost, and bugs introduced, when the program
mistakenly assumes that the network delivers messages in the order in which
they were sent, when in fact the network (like the post office)
does not guarantee this.
For example, consider the following program, where data and data_ready_flag are global pointers to data owned by processor 2, both of which are initially zero:
Processor 1 Processor 2
*data := 1 while (*data_ready_flag != 1) {/* wait for data*/}
*data_ready_flag := 1 print 'data=',*data
From Processor 1's point of view, first *data is set to 1,
then the *data_ready_flag is set.
But Processor 2 may print either data=0 or data=1,
depending on which message from Processor 1 is delivered first.
If data=0 is printed, this is not sequentially consistent with the order
in which Processor 1 has executed its instructions, and probably will
result in a bug. Note that this bug is nondeterministic, i.e. it may or may
not occur on any particular run, because it is timing dependent. These
are among the hardest bugs to find!
This sort of hazard is not an artifact of Split-C, but in fact occurs when programming several shared memory machines with caches, as discussed in Lecture 3. So it is a fact of life in parallel computing.
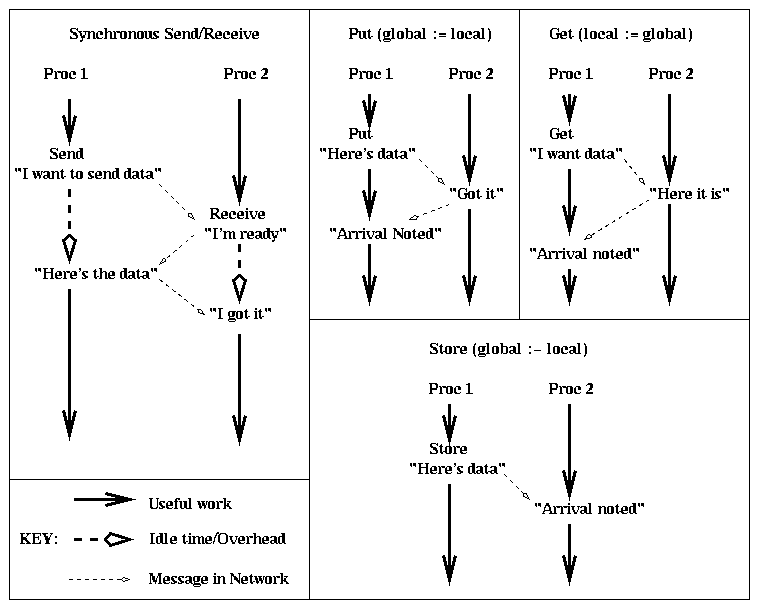
In addition to the split phase assignments put (global := local) and get (local := global), there is one more called store, which is written
global :- local
The difference between store and put is that store provides no
acknowledgement to the sender of the receipt, whereas put does.
This is illustrated by the last figure above.
Thus, store reduces yet further the total number of messages in the
network, which means the network can spend yet more time sending useful
data rather than acknowledgements.
To be able to use the data stored on a processor, one still needs to know whether it has arrived. There are two ways to do this. The simplest way is to call store_sync(n), which waits until n bytes have been stored in the memory of the processor executing store_sync(n). This presumes the parallel algorithm is designed so that one knows how much data to expect.
For example, the following code fragment stores the transpose of the spread array A in B:
static int A[n]::[n], B[n]::[n]
for (i=0; i++; i< n)
B[MYPROC][i] = A[i][MYPROC];
This is a slow implementation because use of "=" in the assignment means
at most one communication occurs at a time.
We may improve this by replacing "=" by ":=":
static int A[n]::[n], B[n]::[n]
for (i=0; i++; i< n)
B[MYPROC][i] := A[i][MYPROC];
sync();
Now there can be several communications going on simultaneously, and one
only has to wait for one's own part of B to arrive before continuing.
But there are still twice as many messages in the network as necessary,
leading us to
static int A[n]::[n], B[n]::[n]
for (i=0; i++; i< n)
B[i][MYPROC] :- A[MYPROC][i];
store_sync(n);
Now there are a minimal number of messages in the system, and one continues
computing as soon as n messages have arrived.
But this code still has a serious bottleneck: the first thing all the processors try to do is send a message to processor 0, which owns B[0][MYPROC] for all MYPROC. This means processor 0 is a serial bottleneck, followed by processor 1 and so on. It is better to have message destinations evenly distributed across all processors. Note that in the following code fragment, for each value of i, the n stores all have different processor destinations:
static int A[n]::[n], B[n]::[n]
for (i=0; i++; i< n)
B[(i+MYPROC) mod MYPROC][MYPROC] :- A[MYPROC][(i+MYPROC) mod MYPROC];
store_sync(n);
It is also possible to ask if all store operations on all processors have completed by calling all_store_sync(). This functions as a barrier, which all processors must execute before continuing. Its efficient implementation depends on some special network hardware on the CM-5 (to be discussed briefly later), and will not necessarily be fast on other machines without similar hardware.
Processor 1 Processor 2
*i = *i + 1 *i = *i + 2
barrier() barrier()
print 'i=', i
Here *i is a global pointer pointing to a location on processor 3.
Recall that either 'i=1', 'i=2' or 'i=3' may be printed,
depending on the order in which the 4 memory accesses occur
(2 gets of *i and 2 puts to *i).
To avoid this, we encapsulate the
incrementation of *i in an atomic operation, which
guarantees that only one processor may increment *i at a time.
static int x[PROCS]:: ;
void add(int *i, int incr)
{
*a = *a + b
}
splitc_main()
{
int *global i = (int *global)(x+3) /* make sure i points to x[3] */
if ( MYPROC == 3 ) *i = 0; /* initialize *i */
barrier(); /* after this, all processors see *i=0 */
if ( MYPROC == 1 )
atomic( add, i, 1 ); /* executed only by processor 1 */
elseif ( MYPROC == 2 )
atomic( add, i, 2 ); /* executed only by processor 2 */
}
Atomic(procedure, arg1, arg2 ) permits exactly one subroutine to execute
procedure( arg1, arg2 ) at a time. Other processors executing
Atomic(procedure, arg1, arg2 ) at the same time queue up, and are permitted
to execute procedure( arg1, arg2 ) one at at time. Atomic procedures should
be short and simple (since they are by design a serial bottleneck), and
are subject to a number of restrictions described in
section 8.1 of
Introduction to Split-C.
Computer science students who have studied operating systems
will be familiar with this approach, which is called
mutual exclusion, since one processor executing the atomic
procedure excludes all others. The body of the atomic procedure
is also sometimes called a critical section.
Here is a particularly useful application of an atomic operation, called a job queue. A job queue keeps a list of jobs to be farmed out to idle processors. The jobs have unpredictable running times, so if one were to simply assign an equal number of jobs to each processor, some processors might finish long before others and so remain idle. This unfortunate situation is called load imbalance, and is clearly an inefficient use of the machine. The job queue tries to avoid load imbalance by keeping a list of available jobs and giving a new one to each processor after it finishes the last one it was doing. The job queue is a simple example of a load balancing technique, and we will study several others. It assumes all the jobs can be executed independently, so it doesn't matter which processor executes which job.
The simplest (and incorrect) implementation of a job queue one could imagine is this:
static int x[PROCS]:: ;
splitc_main()
{
int job_number;
int *global cnt = (int *global)(x); /* make sure cnt points to x[0] */
if ( MYPROC == 0 ) *cnt = 100; /* initialize *cnt to number of
jobs initially available */
barrier();
while ( *cnt > 0 ) /* while jobs remain to do */
{
job_number = *cnt; /* get number of next available job */
*cnt = *cnt - 1; /* remove job from job queue */
work(job_number); /* do job associated with job_number */
}
The trouble with this naive implementation is that two or more processors may
get *cnt at about the same time and get the same job_number to do. This
can be avoided by decrementing *cnt in a critical section:
static int x[PROCS]:: ;
void fetch_and_add_atomic(int proc, void *return_val, int *addr, int incr_val )
{
int tmp = *addr;
*addr = *addr + incr_val;
atomic_return_i(tmp);
}
int fetch_and_add( int *global addr, int incr_val )
{
return atomic_i( fetch_and_add_atomic, addr, incr_val )
}
splitc_main()
{
int job_number;
int *global cnt = (int *global)(x) /* make sure cnt points to x[0] */
if ( MYPROC == 0 ) *cnt = 100; /* initialize *cnt to number of
jobs initially available */
barrier()
while ( *cnt > 0 ) /* while jobs remain to do */
{
job_number = fetch_and_add(cnt,-1); /* get number of next available job */
work(job_number); /* do job associated with job_number */
}
}
Fetch_and_add(addr,incr_val) atomically fetches the old value of
*addr, and increments it by incr_val.
Find the string "splitc_main" to examine the main procedure. The fish are spread among the processors in a spread array allocated by
fish_t *spread fishes = all_spread_malloc(NFISH, sizeof(fish_t));
Here fish_t is a struct (defined near the top of the file) containing the
position, velocity and mass of a fish, and NFISH = 10000 is a constant.
The next line
int num_fish = my_elements(NFISH)
uses an intrinsic function to return the number of
fish stored on the local processor. Then
fish_t *fish_list = (fish_t *)&fishes[MYPROC];
provides a local pointer to the beginning of the local fish.
In other words, the local fish are stored from address
fish_list to fish_list + num_fish*sizeof(fish_t) -1.
The rest of the main routine calls
all_init_fish (num_fish, fish_list) to initialize the local fish,
all_do_display(num_fish, fish_list) to display the local fish periodically, and
all_move_fish (num_fish, fish_list, dt, &max_acc, &max_speed, &sum_speed_sq)
to move the local fish and return their maximum acceleration, etc.
The global reduction operation
max_acc = all_reduce_to_all_dmax(max_acc);
reduces all the local maximum accelerations to a global maximum. The other two
all_reduce_to_all calls are analogous.
all_init_fish() does purely local work, so let us next examine all_do_display. This routine first declares a spread pointer map, and then calls
map = all_calculate_display(num_fish, fish_list);
to compute the 2D image of the fish in a spread array and return a
spread pointer to it in map. The map is displayed by calling
all_display_fish(map);
to pass the map to the host (which handles the X-window display),
doing a barrier to make sure all the processors have passed their
data to the host, and then having only processor 0 display the data via
on_one {X_show();}
all_calculate_display works as follows. on the first call, a spread array of size DISPLAY_SIZE-by-DISPLAY_SIZE (256-by-256) is allocated, with map pointing to it. The statements
for_my_1d(i, DISPLAY_SIZE*DISPLAY_SIZE) {
map[i] = 0; /* blue */ }
barrier();
have each processor initialize its local entries of the spread array to 0
(blue water, i.e. no fish). The Split-C macro for_my_1d loops over just
those values of i from 0 to DISPLAY_SIZE*DISPLAY_SIZE-1 such that
map[i] is stored locally.
The next loop loops over all locally stored fish, computes the scaled coordinates (x_disp,y_disp) of each fish, where 0 <= x_disp , y_disp < DISPLAY_SIZE, and atomically adds 1 to map[x_disp,y_disp] to indicate the presence of a fish at that location (we use poetic license here by addressing map as a 2D array, whereas the code addresses it as a 1D array). The final all_atomic_sync waits until all the processors have finished updating map.
After all_calculate_display returns in all_do_display, map contains an image of the current fish positions, with map[x_disp,y_disp] containing the number of fish at scaled location (x_disp,y_disp). Next, all_do_display calls all_display_fish(map) to transfer the data to the host. The first time all_display_fish is called it has processor 0 initialize the X-window interface, allocates a spread array called old_map to keep a copy of the map from the previous time step, and initializes old_map to 0 (empty). Then, all_display_fish has each processor compare the part of map it owns to the corresponding part of old_map, which it also owns, and if they differ it transfers the new map data to the host for X-window display. This minimizes the number of messages the host has to handle, a serial bottleneck. Finally, map is copied to old_map for the next step.
Procedure all_move_fish does all the work of moving the fish, and is purely local.