
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
Logo is best known as the language that introduced the turtle as a tool for computer graphics. In fact, to many people, Logo and turtle graphics are synonymous. Some computer companies have gotten away with selling products called "Logo" that provided nothing but turtle graphics, but if you bought a "Logo" that provided only the list processing primitives we've used so far, you'd probably feel cheated.
Historically, this idea that Logo is mainly turtle graphics is a mistake. As I mentioned at the beginning of Chapter 1, Logo's name comes from the Greek word for word, because Logo was first designed as a language in which to manipulate language: words and sentences. Still, turtle graphics has turned out to be a very powerful addition to Logo. One reason is that any form of computer graphics is an attention-grabber. But other programming languages had allowed graphics programming before Logo. In this chapter we'll look at some of the reasons why turtle graphics, specifically, was such a major advance in programming technology.
This chapter can't be long enough to treat the possibilities of computer graphics fully. My goal is merely to show you that the same ideas we've been using with words and lists are also fruitful in a very different problem domain. Ideas like locality, modularity, and recursion appear here, too, although sometimes in different guises.
I've been assuming that you've already been introduced to Logo turtle graphics, either in a school or by reading Logo tutorial books. If not, perhaps you should read one of those books now. But just in case, here is a very brief overview of the primitive procedures for turtle graphics. Although some versions of Logo allow more than one turtle, or allow dynamic turtles with programmable shapes and speeds, for now I'll only consider the traditional, single, static turtle.
Type the command cs (short for clearscreen), with no
inputs. The effect of this command is to initiate Logo's graphics
capability. A turtle will appear in the center of a graphics window.
(Depending on which version of Logo you have, the turtle may look like an
actual animal with a head and four legs or--as in Berkeley Logo--it may be
represented as a triangle.) The turtle will be facing toward the top of the
screen. Any previous graphic drawing will be erased from the screen and
from the computer's memory.
The crucial thing about the turtle, which distinguishes it from other metaphors for computer graphics, is that the turtle is pointing in a particular direction and can only move in that direction. (It can move forward or back, like a car with reverse gear, but not sideways.) In order to draw in any other direction, the turtle must first turn so that it is facing in the new direction. (In this respect it is unlike a car, which must turn and move at the same time.)
The primary means for moving the turtle is the forward command,
abbreviated fd. Forward takes one input, which must be a
number. The effect of forward is to move the turtle in the
direction it's facing, through a distance specified by the input. The
unit of distance is the "turtle step," a small distance that depends
on the resolution of your computer's screen. (Generally, one turtle
step is the smallest line your computer can draw. This is
slightly oversimplified, though, because that smallest distance may be
different in different directions. But the size of a turtle step does
not depend on the direction; it's always the same distance for
any given computer.) Try typing the command
forward 80 |  |
Since the turtle was facing toward the top of the screen, that's the way it moved. The turtle should now be higher on the screen, and there should be a line behind it indicating the path that it followed.
The first turtles were actual robots that rolled along the floor. They got the name "turtle" because of the hard shells surrounding their delicate electronic innards. A robot turtle has a pen in its belly, which it can push down to the floor, or pull up inside itself. When the pen is down, the turtle draws a trace of its motion along the floor.
When talking about the screen turtle, it's customary to think of the screen as a kind of map, representing a horizontal floor. Therefore, instead of referring to the screen directions as "up," "down," "left," and "right," we talk about the compass headings North, South, West, and East. Your turtle is now facing North. Besides fitting better with the turtle metaphor, this terminology avoids a possible confusion: the word "left" could mean either the turtle's left or the screen's left. (They're the same direction right now, but they won't be the same after we turn the turtle.) To avoid this problem, we use "West" for the left edge of the screen, and reserve the word "left" for the direction to the left of whichever way the turtle is facing.
Logo provides primitive commands to raise and lower the turtle's pen.
The command penup (abbreviated pu) takes no inputs; its
effect is to raise the pen. In other words, after you use this
command, any further turtle motion won't draw lines. Try it now:
penup forward 30 |  |
Similarly, the command pendown (pd) takes no
inputs, and lowers the pen. Here's a procedure you can try:
to dash :count repeat :count [penup forward 4 pendown forward 4] end ? clearscreen dash 14 |  |
The command back (or bk) takes one input, which must be a
number. The effect of back is to move the turtle backward by
the distance used as its input. (What do you think fd and
bk will do if you give them noninteger inputs? Zero inputs?
Negative inputs? Try these possibilities. Then look up the commands
in the reference manual for your version of Logo and see if the
manual describes the commands fully.)
To turn the turtle, two other commands are provided. Left
(abbreviated lt) takes one input, which must be a number. Its
effect is to turn the turtle toward the turtle's own left.
The angle through which the turtle turns is the input; angles are
measured in degrees, so
left 360
will turn the turtle all the way around. (In other words, that
instruction has no real effect!) Another way of saying that the turtle
turns toward its own left is that it turns counterclockwise.
The command right (or rt) is just like left, except
that it turns the turtle clockwise, toward its own right.
»Clear the screen and try this, the classic beginning point of Logo turtle graphics:
repeat 4 [forward 100 right 90]
This instruction tells Logo to draw four lines, each 100 turtle steps long, and to turn 90 degrees between lines. In other words, it draws a square.
There are many more turtle procedures provided in Logo, but these are the fundamental ones; with them you can go quite far in generating interesting computer graphics. If you haven't had much experience with turtle graphics before, you might enjoy spending some time exploring the possibilities. There are many introductory Logo turtle graphics books to help you. Because that part of Logo programming is so thoroughly covered elsewhere, I'm not going to suggest graphics projects here. Instead I want to go on to consider some of the deeper issues in computer programming that are illuminated by the turtle metaphor.
Earlier we considered the difference between local variables, which are available only within a particular procedure, and global variables, which are used throughout an entire project. I've tried to convince you that the use of local variables is a much more powerful programming style than one that relies on global variables for everything. For one thing, local variables are essential to make recursion possible; in order for a single procedure to solve a large problem and a smaller subproblem simultaneously, each invocation of the procedure must have its own, independent variables. But even when recursion is not an issue, a complex program is much easier to read and understand if each procedure can be understood without thinking about the context in which it's used.
The turtle approach to computer graphics embodies the same principle of
locality, in a different way. The fact that the turtle motion
commands (forward and back) and the turtle turning commands (
left and right) are all turtle-relative means that a
graphics procedure need not think about the larger picture.
To understand what that means, you should compare the turtle metaphor with the other metaphor that is commonly used in computer graphics: Cartesian coordinates. This metaphor comes from analytic geometry, invented by Rene Descartes (1596-1650). The word "Cartesian" is derived from his name. Descartes' goal was to use the techniques of algebra in solving geometry problems by using numbers to describe points. In a two-dimensional plane, like your computer screen, you need two numbers to identify a point. These numbers work like longitude and latitude in geography: One tells how far the point is to the left or right and the other tells how high up it is.
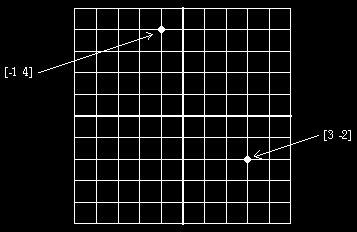
This diagram shows a computer screen with a grid of horizontal and
vertical lines drawn on it. The point where the two heavy lines meet
is called the origin; it is represented by the numbers
[0 0]. For other points the first number (the
x-coordinate) is the horizontal distance from the origin to the
point, and the second number (the y-coordinate) is the
vertical distance from the origin to the point. A positive
x-coordinate means that the point is to the right of the origin; a
negative x-coordinate means that the point is to the left of the
origin. Similarly, a positive y-coordinate means that the point is
above the origin; a negative y-coordinate puts it below the origin.
Logo does allow you to refer to points by their Cartesian coordinates,
using a list of two numbers. The origin is the point where the turtle
starts when you clear the screen.
The primary tool for Cartesian-style graphics in Logo is the command
setpos (for set position). Setpos
requires one input, which must be a list of two numbers. Its effect
is to move the turtle to the point on the screen at those
coordinates. If the pen is down, the turtle draws a line as it moves,
just as it does for forward and back. Here is how you
might draw a square using Cartesian graphics instead of turtle
graphics:
clearscreen setpos [0 100] setpos [100 100] setpos [100 0] setpos [0 0]
Do you see why I said that the Cartesian metaphor is global, like the use of global variables? Each instruction in this square takes into account the turtle's position within the screen as a whole. The "point of view" from which we draw the picture is that of an observer standing above the plane looking down on all of it. This observer sees not only the turtle but also the edges and center of the screen as part of what is relevant to drawing each line. By contrast, the turtle geometry metaphor adopts the point of view of the turtle itself; each line is drawn without regard to where the turtle is in global terms.
Using the turtle metaphor, we can draw our square (or any other figure
we can program) anywhere on the screen at any orientation. First
I'll write a square command:
to square :size repeat 4 [forward :size right 90] end
Now here's an example of how square can be used in
different positions and orientations:
to face pendown square 100 penup forward 20 right 90 forward 25 pendown forward 50 penup back 75 left 90 forward 65 right 90 forward 20 pendown square 15 penup forward 45 pendown square 15 penup back 15 right 90 forward 20 left 45 pendown square 20 end |  |
The head and the eyes are upright squares; the nose is a square at an angle (a diamond). To write this program using Cartesian graphics, you'd have to know the absolute coordinates of the corners of each of the squares. To draw a square at an unusual angle, you'd need trigonometry to calculate the coordinates.
»Here is another demonstration of the same point. Clear the screen and type this instruction:
repeat 20 [pendown square 12 penup forward 20 right 18]
You'll see squares drawn in several different orientations. This would not be a one-line program if you tried to do it using the Cartesian metaphor!
From a turtle's-eye point of view, drawing an upright square is the same as drawing a diamond. It's only from the global point of view, taking the borders of the screen into account, that there is a difference.
From the global point of view how can we think about that
difference? How do we describe what makes the same procedure
sometimes draw one thing (an upright square) and sometimes another (a
diamond)? The answer, in the most general terms, is that the result
of the square command depends on the past history of the
turtle--its twists and turns before it got to wherever it may be
now. That is, the turtle has a sort of memory of past events.
But what matters is not actually the turtle's entire past history. All that counts is the turtle's current position and its current heading, no matter how it got there. Those two things, the position and the heading, are called the turtle's state. It's a little like trying to solve a Rubik's Cube; you may have turned part of the cube 100 times already, but all that counts now is the current pattern of colors, not how you got there.
I've mentioned the setpos command, which sets the turtle's
position. There is also a command setheading (abbreviated
seth) to set the
heading. Setheading takes one input, a number. The effect is to turn
the turtle so that it faces toward the compass heading specified by
the number. Zero represents North; the heading is measured in degrees
clockwise from North. (For example, East is 90; West is 270.) The
compass heading is different from the system of angle measurement used
in analytic geometry, in which angles are measured counterclockwise
from East instead of clockwise from North.
In addition to commands that set the turtle's state, Logo provides
operations to find out the state. posPos is an operation
with no inputs. Its output is a list of two numbers, representing the
turtle's current position. headingHeading is also an
operation with no inputs. Its output is a number, representing the turtle's
current heading.
Remember that when you use these state commands and operations, you're
thinking in the global (Cartesian) style, not the local (turtle)
style. Global state is sometimes important, just as global variables
are sometimes useful. If you want to draw a picture containing three
widgets, you might use setpos to get the turtle into position
for each widget. But the widget procedure, which draws each
widget, probably shouldn't use setpos. (You might also use
setpos extensively in a situation in which the Cartesian
metaphor is generally more appropriate than the turtle metaphor, like
graphing a mathematical function.) As in the case of global
variables, you'll be most likely to overuse global graphics style if
you're accustomed to BASIC computer graphics. A good rule of
thumb, if you're doing something turtleish and not graphing a function, is
that you shouldn't use setpos with the pen down.
»Do you see why?
Very young children often begin playing with Logo simply by moving the
turtle around at random. The resulting pictures usually don't look
very interesting. You can recapture the days of your youth by
alternating forward and right commands with arbitrary inputs.
Here is a sample, which I've embodied in a procedure:
to squiggle forward 100 right 135 forward 40 right 120 forward 60 right 15 end | 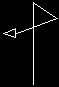
|
This isn't a very beautiful picture. But something interesting happens when you keep squiggling repeatedly:
repeat 20 [squiggle] |  |
Instead of filling up the screen with hash, the turtle draws a symmetrical shape and repeats the same path over and over! Let's try another example:
to squaggle forward 50 right 150 forward 60 right 100 forward 30 right 90 end | 
|
Squiggle turns into a sort of fancy square when you repeat it;
squaggle turns into an 18-pointed pinwheel. Does every possible
squiggle produce a repeating pattern this way? Yes. Sometimes you
have to repeat the procedure many times, but essentially any
combination of forward and right commands will eventually retrace
its steps. (There's one exception, which we'll talk about shortly.)
To see why repetition brings order out of chaos, we have to think about a simpler Logo graphics procedure that is probably very familiar to you:
to poly :size :angle forward :size right :angle poly :size :angle end
Since this is a recursive procedure without a stop rule, it'll keep running forever. You'll have to stop it by pressing the BREAK key, or command-period, or whatever your particular computer requires. The procedure draws regular polygons; here are some examples to try:
poly 100 90 poly 80 60 poly 100 144
A little thought (or some experimentation) will show you that
the size input makes the
picture larger or smaller but doesn't change its shape. The shape is
entirely controlled by the angle input.
»What angle would you pick to draw a triangle? A pentagon? How do you know?
The trick is to think about the turtle's state. When you finish drawing a polygon, the turtle must return to its original position and its original heading in order to be ready to retrace the same path. To return to its original heading, the turtle must turn through a complete circle, 360 degrees. To draw a square, for example, the turtle must turn through 360 degrees in four turns, so each turn must be 360/4 or 90 degrees. To draw a triangle, each turn must be 360/3 or 120 degrees.
»Now explain why an angle input of 144 draws a star!
Okay, back to our squiggles. Earlier, I said that the only thing we
have to remember from the turtle's past history is the change in its
state. It doesn't matter how that change came about. When you draw a
squiggle, the turtle moves through a certain distance and turns
through a certain angle. The fact that it took a
roundabout path doesn't matter. As it happens, squiggle turns
right through 135+120+15 degrees, for a total of 270. This is
equivalent to turning left by 90 degrees. That's why repeating
squiggle draws something shaped like a square.

»What about squaggle? If repeating it draws a figure with
18-fold symmetry, then its total turning should be 360/18 or 20 degrees. Is
it?
»Here's another bizarre shape. See if you can predict what kind of symmetry it will show before you actually repeat it on the computer.
to squoggle forward 50 right 70 forward 10 right 160 forward 35 right 58 end | 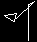
|
Suppose you like the shape of squiggle, but you want to draw a
completed picture that looks triangular (3-fold symmetry) instead of
square (4-fold). Can you do this? Of course; you can simply change
the last instruction of the squiggle procedure so that the total
turning is 120 degrees instead of 90. (Go ahead, try it. Be careful
about left and right.)
But it's rather an ugly process to have to edit squiggle in
order to change not what a squiggle looks like but how the squiggles
fit into a larger picture. For one thing, it violates the idea of
modularity. Squiggle's job should just be drawing a squiggle,
and there should be another procedure, something like poly,
that combines squiggles into a symmetrical pattern. For another,
people shouldn't have to do arithmetic; computers should do the
arithmetic!
To clean up our act, I'm going to start by writing a procedure that
can draw an arbitrary squiggle but without changing the turtle's
heading. It's called protect.heading because it protects the
heading against change by the squiggle procedure.
to protect.heading :squig local "oldheading make "oldheading heading run :squig setheading :oldheading end
This procedure demonstrates the use of heading
and setheading. We remember the turtle's initial heading
in the local variable oldheading. Then we carry out whatever squiggle
procedure you specify as the input to protect.heading. (The
run command takes a Logo instruction list as input and evaluates
it.) Here is how you can use it:
protect.heading [squiggle] protect.heading [squaggle]
Notice that what is drawn on the screen is the same as it
would be if you invoked squiggle or squaggle directly; the
difference is that the turtle's final heading is the same as its
initial heading.

Now we can use protect.heading to write the decorated-poly
procedure that will let us specify the kind of symmetry we want:
to spin :turns :command repeat :turns [protect.heading :command right 360/:turns] end
»Try out spin with instructions like these:
spin 3 [squiggle] spin 5 [squiggle] spin 4 [squaggle] spin 6 [squoggle] spin 6 [fd 40 squoggle] spin 5 [pu fd 50 pd squaggle] | 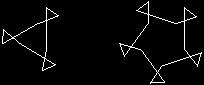
|
Isn't that better?
I mentioned that there is an exception to the rule that every squiggle will eventually retrace its steps if you repeat it. Here it is:
to squirrel forward 40 right 90 forward 10 right 90 forward 15 right 90 forward 20 right 90 end | 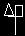
|
»Try repeating squirrel 20 times. You'll find that
instead of turning around to its original position and heading, the
turtle goes straight off into the distance. Why? (Squiggle had
four-fold symmetry because its total turning was 90 degrees. What is
the total turning of squirrel?) Of course, if you use
squirrel in the second input to spin, it will perform like the
others, because spin controls the turtle's heading in that case.
I've been using random squiggles with silly names to make
the point that by paying attention to symmetry, Logo can make
a silk purse from a sow's ear. But of course there is no reason not
to apply spin to more carefully designed pieces. Here's one I
like:
to fingers :size penup forward 10 pendown right 5 repeat 5 [forward :size right 170 forward :size left 170] left 5 penup back 10 pendown end spin 4 [fingers 50] spin 10 [fingers 30] | 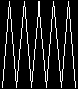
|
I'd like to write a procedure to draw this picture of a tree:
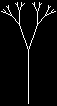
The trick is to identify this as a recursive problem. Do you see the smaller-but-similar subproblems? The tree consists of a trunk with two smaller trees attached.

So a first approximation to the solution might look like this:
to tree :size forward :size left 20 tree :size/2 right 40 tree :size/2 end
If you try running this procedure, you'll see that we still
have some work to do. But let me remind you that an unfinished
procedure like this isn't a mistake; you shouldn't feel that
you have to have every detail worked out before you first touch the
keyboard. The first obvious problem is that there is no stop rule, so
the procedure keeps trying to draw smaller and smaller subtrees. What
should the limiting condition be? In this case there is no obvious
end, like the butfirst of a word becoming empty.
There are two approaches we could take to limiting the number of
branches of the tree. One approach would be to choose explicitly how
deep we want to get in recursive invocations. We could do this by
adding another input, called depth, that will be the number of
levels of recursion to allow:
to tree :depth :size if :depth=0 [stop] forward :size left 20 tree (:depth-1) :size/2 right 40 tree (:depth-1) :size/2 end
The other approach would be to keep letting the branches get smaller until they go below a reasonable minimum:
to tree :size if :size<4 [stop] forward :size left 20 tree :size/2 right 40 tree :size/2 end
Either approach is reasonable. I'll choose the second one just because it seems a little simpler. The cost of that choice is somewhat less control over the final picture; I'm not sure if it'll have exactly the number of branches I originally planned.
The modified procedure does come to a halt now, but it still doesn't
draw the tree I had in mind. The problem is that this version of
tree is not state-invariant: it doesn't leave the turtle with
the same position and heading that it had originally. That's
important because when tree says
tree :size/2 right 40 tree :size/2
the assumption is that at the end of the first smaller tree the turtle will be back at the top of the main trunk, in position to draw the second subtree. We can fix the problem by making the turtle climb back down the trunk (of each subtree):
to tree :size if :size<4 [stop] forward :size left 20 tree :size/2 right 40 tree :size/2 left 20 back :size end
Voila! If you try tree 50 you'll see something like the
picture I had in mind.
You're probably thinking that this "tree" doesn't look very tree-like. There are several things wrong with it: It's too symmetrical; it doesn't have enough branches; the branches should grow partway up the trunk as well as at the top. But all of these problems can be solved by adding a few more steps to the procedure:
to tree :size if :size < 5 [forward :size back :size stop] forward :size/3 left 30 tree :size*2/3 right 30 forward :size/6 right 25 tree :size/2 left 25 forward :size/3 right 25 tree :size/2 left 25 forward :size/6 back :size end | 
|
We can embellish the tree as much as we want. The only requirement is that the procedure be state-invariant: The turtle's final position and heading must be the same as its beginning position and heading.
Because I chose to use a minimum length as the stopping condition, the shape of the tree depends on the size of its trunk. That's slightly unusual in turtle graphics programs, which usually draw the same shape regardless of the size.
A recursively-defined shape (one that contains smaller versions of itself)
is called a fractal. Until the 1970s, hardly anybody explored
fractals except for kids learning Logo and a few recreational mathematicians.
Today, however, fractals have become important becase movie producers are
using computer graphics as an alternative to expensive sets and models for
fancy special effects. It turns out that programs like tree are the
secret of drawing realistic clouds, mountains, and other natural
backgrounds with a computer.
»If you want another challenging fractal project, try writing a program to produce these fractal snowflakes:
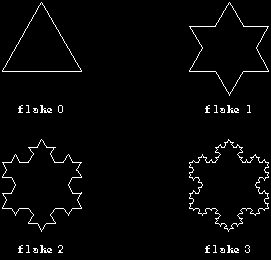
If you're interested in an intellectually rigorous exploration of turtle geometry, continuing along the lines I've started here, read Turtle Geometry, Abelson and diSessa (MIT Press, 1981). I learned many of the things in this chapter from them. It's a hard book but worth the effort.
The standard reference book on fractals is The Fractal Geometry of Nature, by Benoit Mandelbrot (W. H. Freeman, 1982). Dr. Mandelbrot gave fractals their name and was the first to see serious uses for them.
Brian Harvey,
bh@cs.berkeley.edu