μ & σ
Uncertainty Sets for Image Classifiers using Conformal Prediction
@misc{angelopoulos-sets,
title={Uncertainty Sets for Image Classifiers using Conformal Prediction},
author={Angelopoulos, Anastasios Nikolas and Bates, Stephen and Malik, Jitendra and Jordan, Michael I.},
url={https://arxiv.org/abs/2009.14193},
journal={arXiv:2009.14193},
year={2020}
}
Summary
This blog post will teach you an algorithm which quantifies the uncertainty of any classifier on any dataset in finite samples for free.
The algorithm, called RAPS, modifies the classifier to output a predictive set containing the true label with a user-specified probability, such as 90%.
This coverage level is formally guaranteed even when the dataset has a finite number of samples.
Empirically, the sets are also relatively small on Imagenet with a ResNet-152, which suggests they will be effective to quantify uncertainty in high-risk settings such as medical diagnostics.
Our GitHub implementation allows you to use the method on any classifier, and you can try it out in Colab without downloading anything.
tl; dr
You are given a small holdout set of labelled images
Algorithm 1 RAPS
1:procedure RAPS(the calibration dataset, the model, the new image)
2:calibrate: perform Platt scaling on the model using the calibration set.
3:get conformal scores: For each image in the training set, define
4:find the threshold: assign
5:predict: Output the
6:end procedure
Intuitively, a high RAPS method easily wraps around any classifier with our GitHub.
After installing our dependencies, you can conformalize your pretrained model and output a predictive set with, e.g.,
model = ConformalModel(model, calib_loader, alpha=0.1, lamda_criterion='size')
logits, raps_sets = model(x)
The easiest place to start is our Colab, where you can try out RAPS without installing anything:
Motivation
Imagine you are a doctor making a high-stakes medical decision based on diagnostic information from a computer-vision classifier. What would you want the classifier to output in order to make the best decision?
As a doctor, your primary objective is to ensure the health of your patient, which requires ruling in or ruling out harmful diagnoses.
In other words, even if the most likely diagnosis is a stomach ache, it is equally or more important to rule out stomach cancer.
Therefore, you would want the classifier to give you actionable uncertainty quantification, such as a set of predictions that provably covers the true diagnosis with a high probability (e.g. 90%).
This is called a prediction set (see Figure 2), and it is analogous to a confidence interval for black box classifiers like neural networks.
The RAPS paper describes a new way to construct prediction sets from any pre-trained image classifier that have exactly the right confidence and small size.
RAPS is as simple as Platt scaling and computationally trivial.
Objectives
RAPS with a ResNet-152 at the 95% level. Underneath each class is the temperature-scaled softmax score of that class. Notice that they do not sum to 95%. As a scientist looking at these sets, you might flag all predictions that have large sets to take a closer look, since the model's top-1 answer could be unreliable.We are given the following:
- a calibration dataset,
- a pretrained model,
- and a new example,
We would like to predict a set
Subject to the coverage constraint, we would like the sets to be small on average.
Finally, we want them to be adaptive: the sets should be smaller for easy examples than for hard ones.
RAPS learns
RAPS procedure achieves exact coverage and has 5-10x smaller sets than competing methods. All methods use a ResNet-152 as the base classifier, and results are reported for 100 random splits of Imagenet-Val, each of size 20K. See the paper for details.The Naive Algorithm
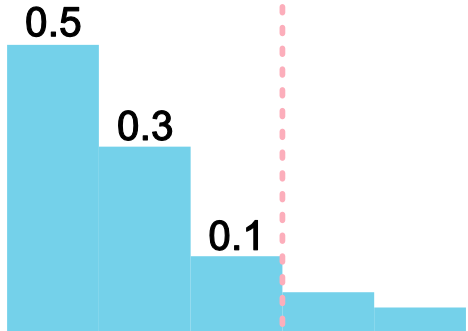
One naive approach is to assemble the set by including classes from highest to lowest probability (e.g. after Platt scaling and a softmax function) until their sum just exceeds
Algorithm 2 naive
1:procedure naive(the calibration dataset, the model, the new image)
2:Perform Platt scaling on the model using the calibration dataset.
3:Compute the softmax scores by running the model on the new image.
4:Chosose classes from highest to lowest score until their total score just exceeds
5:end procedure
There are two problems with the naive method: first, the probabilities output by CNNs are known to be incorrect, so the sets do not achieve coverage. Second, for examples where the model is not confident, the naive strategy must select many classes before it reaches the desired confidence level, leading to a large set size. Temperature scaling cannot solve this problem, since it only calibrates the score of the top class, and it is intractable to calibrate the rest. Perhaps surprisingly, even if all scores were perfectly calibrated, naive still would not achieve coverage.
Regularized adaptive prediction sets
Conformal prediction is a simple idea at heart.
Instead of taking the softmax scores at face value, we learn a new threshold using the calibration dataset.
For example, with APS).
APS is a special case of RAPS with APS provably achieves exact coverage.
However, APS has a problem in practice: the average set size is quite large.
Deep learning classifiers suffer from a permutation problem: the scores of the less confident classes (e.g. classes 10 through 1000) are not reliable probability estimates.
The ordering of these classes is primarily determined by noise, so APS has to take very large sets for some difficult images.
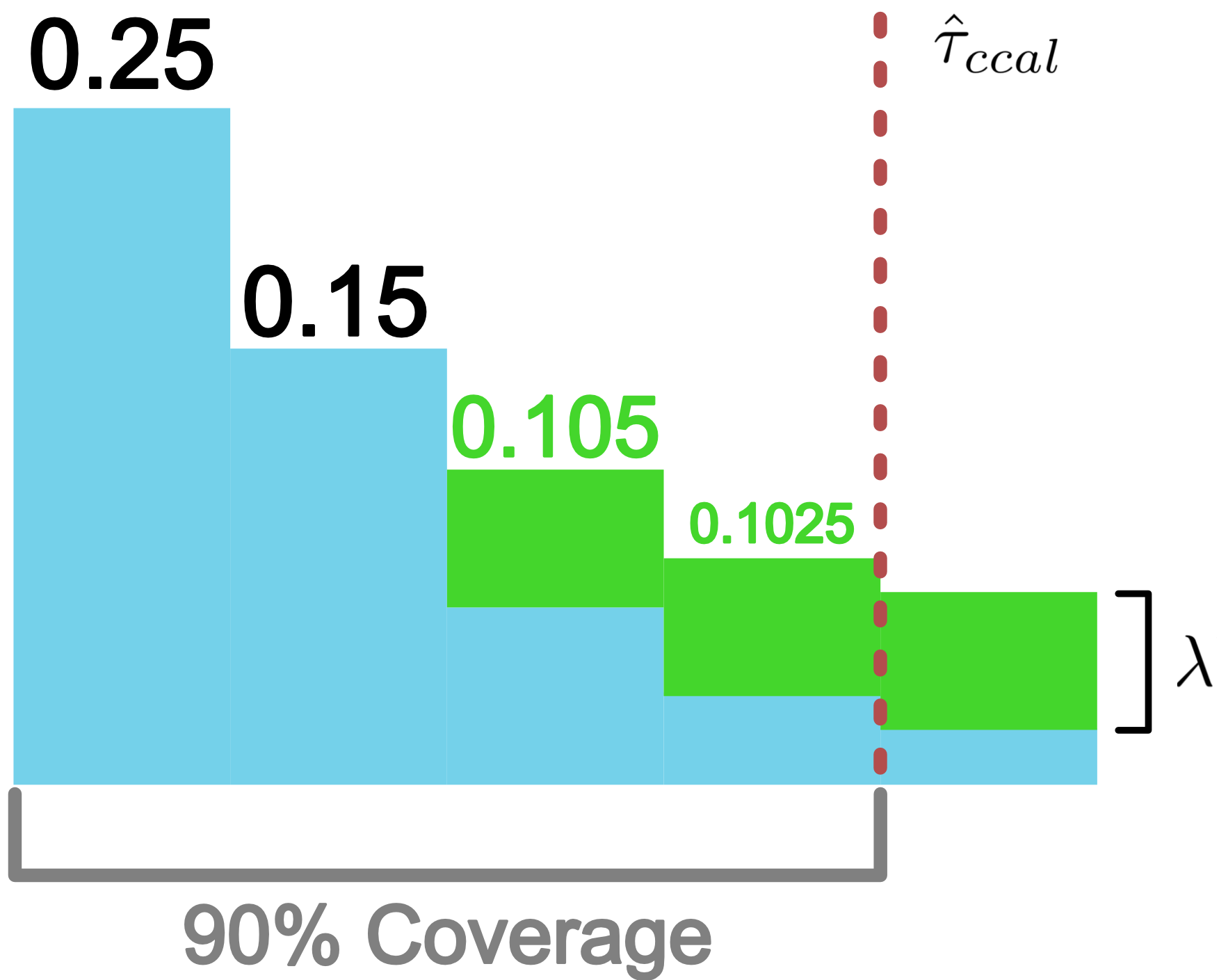
The RAPS procedure (detailed in Algorithm 1) discourages these overly large sets with regularization.
Every class beyond the RAPS achieves the same coverage, as we show below:
APS or RAPS. Then we have the following coverage guarantee:
RAPS paper.
Results
All experiments in our paper can be reproduced exactly using our GitHub.
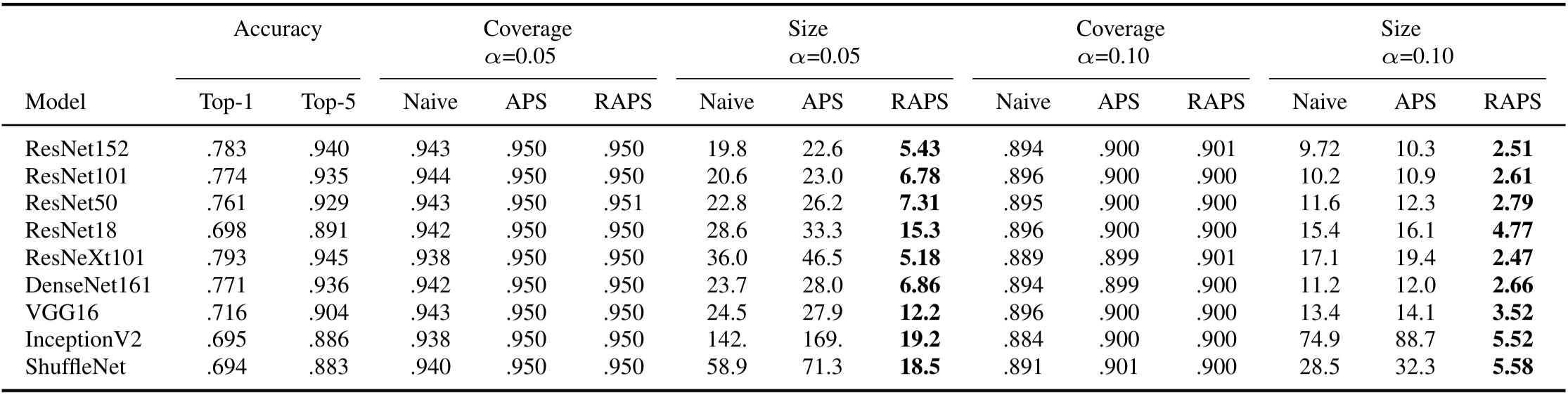
naive, APS, and RAPS sets for nine different Imagenet classifiers.
The median-of-means for each column is reported over 100 different trials. We used parameters
In our experiments, we studied the performance of the predictive sets from naive, APS and RAPS on Imagenet and Imagenet-V2.
In broad strokes, naive does not achieve coverage, and has large sets; APS has exact coverage, but even larger sets.
RAPS achieves coverage with sets 5-10x smaller than APS.
In the table above, we show the numerical results on Imagenet; more experiments probing our method are in the paper.
This method enables a researcher to take any base classifier and return predictive sets guaranteed to achieve a pre-specified error level, such as 90%, while retaining small average size. It is simple to deploy, so it is an attractive, automatic way to quantify the uncertainty of image classifiers, an essential task in settings like medical diagnostics, self-driving vehicles, and flagging dangerous internet content. Predictive sets in computer vision have many further uses, since they systematically identify hard test-time examples. In active learning, finding such examples reduces the number of points that must be labelled. In a different direction, one can improve efficiency of a classifier by using a cheap classifier to output a prediction set first, and an expensive one only when the cheap classifier outputs a large set (a cascade). Finally, one can use predictive sets during model development to identify failure cases and outliers. This helps probe the model's weaknesses, suggesting strategies for improving its performance.
Congratulations for reaching the end of the blog post; now go try out our model on Colab!