CS 184: COMPUTER GRAPHICS

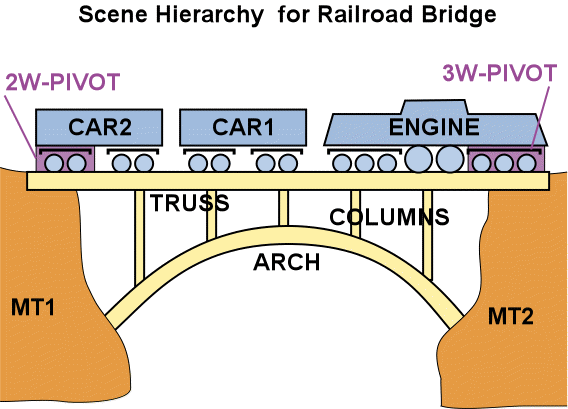
PROBLEM # 1:

Draw a reasonable scene hierarchy for the scene on the left, using all the named entities.

PROBLEM # 2:

Assume a scene has a bright red triangle in it.

Try to list all the reasons why the display of that scene might NOT show any bright red pixels.

PREVIOUS < - - - - > CS 184 HOME < - - - - > CURRENT < - - - - > NEXT

Answer to Problem # 1

A reasonable scene hierarchy that takes into account the construction and the coupling of the engine and the various cars.

Answer to Problem # 2: Reasons why there may be no red pixels:

Triangle is not visible because: -- outside view window (2D), -- too close or too far (3D clipping), -- behind something, -- seen from backside.
Triangle is not rendered because: -- it is too small (missed by all sampling points), -- is below LOD cutoff.
Triangle is not illuminated because: -- no lights, -- in shadow.
Color of the triangle is changed because: -- it is illuminated with colored lights, -- it is seen through a colored filter, -- or through colored fog.
Color of the triangle is changed because: -- it is transparent itself and affected what is behind it, -- it is so out-of-focus and blurred that it becomes "transparent".
The display is Black+White only.

Lecture #8 -- Wed 2/18/2009.

Crucial Concepts from Last Lecture:

Complex scenes are described using hierarchically nested groups of objects (and of other groups) with relative transformations.
Entities that transform together should be grouped together.
An object or group of objects can be instantiated multiple times -- in different places, with different orientations, and different scales.
Different properties get inherited differently down the hierarchy.
The conceptual scene structure is expressed in a corresponding scene graph, which can also be captured in a scene description file:
(G group_A
(I inst_1 geom   (Xform A)   (Xform B)   (Xform C) )       ## should result in:   [Xform C] * [Xform B] * [Xform A] * [geom]
    (I   inst_2 bird (S 1.1 1.6 )   (T 5 3.4 )   (color 1 0.8 0.2 )   )     ## stretched, orange bird;
    (I   inst_3 flock (S 0.8 0.8 )   (T {t*0.2} {4+t*0.1}) )     ## shrunk, uncolored flock of birds, moving to the right and up;
    (I inst_4 UFO (R {t*20} )   (T 8 9 ) (color {sin(t*45*dgr)} {cos(t*66*dgr)} 0.2 ) ) ## UFO, rotating 20 degrees per frame around its center, and changing color.
)
In a classical rendering pipeline this scene graph will be traversed and expanded (flattened) into a full scene tree,
   and every leaf will be properly transformed and projected onto the image plane.
Here is another example of a hierarchical ccene: 18-Wheeler
Discuss what needs to be done and how hierarchy needs to get modified when there is a flat tire.

Rendering by Ray-Casting

Rendering Principles: Comparison of Physical Camera, Clasical Rendering Set-up, and Ray-Casting

Ray-casting: For each pixel on the display screen, shoot a ray from the eye into the scene and determine what it hits, and what color we should put there.
The apparant color of a particular spot in the scene depends on its surface properties, on what light illuminates it, and how the re-emitted light is transformed on the way to the eye/camera.
That is what we focus on in Assignment#4. Schematic of the ray-tracer program.
We will use just a few spheres, so it is easy to determine what any ray hits; -- but spheres can look quite different depending on surface properties and lighting conditions.

Color, Lighting, Shading

CLARIFICATION OF TERMS:

Color is represented with 3 components: RED, GREEN, BLUE, or (RGB) for short. Almost all CG systems work with a 3-vector color basis.
This works because the human visual system has three types of color receptors (more later in the semester).
A surface color, is characterized by the mixture of RGB colors that get reflected when the surface is illuminated with white light ( R=1; G=1; B=1 ).

Illumination (lighting) models: tell us what brightness and what color to expect (physically) on each surface.

Shading / rendering: concerns (efficient) techniques to produce the apparent brightness values on the display.
For instance: To give the appearance of smooth and smoothly colored objects, we may calculate each pixel color as a weighted blend of the colors of nearby vertices.
For simplicity (and assuming that the color differences are not too large), we interpolate the three RGB components separately.
In the context of scan-line based rasterization,
we simply do a linear interpolation along the polyhedron edges, and a linear interpolation across a face from the left edge to right edge along the current scan line.
This bi-linear interpolation of color (and brightness) differs somewhat from the interpolation of z-depth -- which we assumed to be a planar function.
The shading/illumination function is NOT typically planar !
Extra Notes on Scan-Line Algorithms

But first we need to determine the intensities (color) at all the vertices of the object. For that we need an illumination / lighting model.

Lights and Illumination

Definition of important directions and unit vectors: L, V, N, R, H.
Preview of all the coefficients that you will see shortly: C's and K's

Types of Light Sources: Light source models and their key parameters (SLIDE notation)

Ambient Light (e.g., sky): I_amb,C_{light (r,g,b).}

Directional Light (e.g., sun): I_dir,Clight (r,g,b). -- Calculate: L.

Point Light (e.g., candle): I_point,Clight (r,g,b), d0, n1. -- Calculate: L, d.

Spot Light (e.g., stage light): I_spot,Clight (r,g,b), d0, n1, n2. -- Calculate: L, D, d.

Superposition Law: Calculate the effects of each light individually and sum all the resulting effects. (I.e., there is no interaction between photons).

Lighting /(Surface) Models

Illumination (Lighting / Surface) models: They tell us what brightness and what color to expect (physically) at a surface point.

1. Lambert Surfaces

This is an idealization of diffusely reflecting (chalky) surfaces.
Their main advantage is that the apparent brightness of any spot on the surface is viewer-independent.

LAMBERT SURFACES -- what we see: Formula that shows view-angle independence.

LAMBERT PHYSICS -- why that is so: Show where the cosine factors are coming from and why they cancel:

Light absorption falls off with the cosine of the angle between light and face normal. This is because a surface at a non-perpendicular angle in a flux of photons captures fewer photons (by a cos- factor), since it exposes a smaller cross sectional area to the photon stream. This effect is viewer independent and can be pre-calculated once at scene construction time.

All the lighting energy that hits the surface gets absorbed temporarily, then some percentage gets reemitted.
The percentage of light re-emitted in a particular direction depends on the properties of the surface, e.g., K_d, C_d {R,G,B};
For Lambertian (chalky) surfaces the re-emission probability has broad distribution which has a maximum perpendicular to surface; it falls off with the cos of the angle away from the normal. The reason is that grazing photons have a hard time escaping the "rugged" chalky surface, i.e., they get trapped again by protrusions.

Emission probability: cos-factor-emit

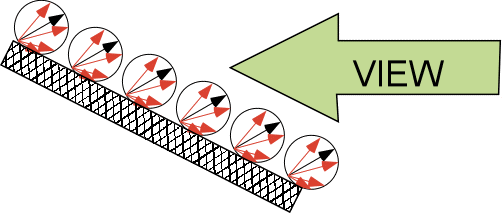
and Slanted viewing situation: cos-factor-view

When viewing a surface from an arbitrary angle, this fall-off is compensated by the fact that, as we see the surface more foreshortened, we also crowd more emission centers into the apparent solid angle of our viewing field by 1/cos . ( DEMO with black page with white dots.)
Thus a chalky Lambert surface has an apparent brightness that does not vary with view direction.
Flat polygons will appear of uniform brightness when uniformly lit, and they all keep a constant brightness from all view points!
Thus the output spans for a flat polygon can be of uniform brightness from left to right edge (even under close-up, wide-angle viewing!).
Note: Our sun is also a "Lambert type emitter" -- Thus its apparent intensity is constant across the whole perceived "flat disk".

When do chalky spheres appear as uniformly shaded (apparently flat) disks ?
When do they appear as depth modulated 3D objects with varying brightness ?

2. Perfect Mirrors

Shiny surface with complete specular reflection.
Reflection laws: L, N, R in same plane; incident angle = reflection angle (against normal), but R is on the other side of the normal vector.
The result is, that we see a bright reflection spot where the camera lies in the R direction; everywhere else the surface is dark !

3. Phong Approximation of Real Surfaces

Real surfaces are a mixture of chalky properties and of a dull, dusty mirror. They have some diffuse as well as some specular reflection.
==> The reflected beam is spread out in a small angle around the unit vector R.
Phong model: Models the reflective component on a real surface as a "fuzzy club" shape around R
Its intensity falls of with a user definable power of the cosine of the deviation angle from the ideal R direction.

Phong Illumination/Lighting/Surface Model: Show effect of exponent of cosine function.

Phong Highlight on flat glossy surface:
Even uniform directional light falling on a flat surface can produce non-uniform brightness, if surface is partially reflective and we use a Phong illumination model.

4. Advanced Approximations of Real Surfaces:

Real materials are more complicated: Spreading of light (Phong exponent) may depend on:
   -- the incident angle {Torrence Sparrow model }.
   -- the color of the light {spectral behavior; different wavelenghts get absorbed/reflected differently.
   -- the surface material:
        -> in metal, reflected light penetrates deeper into substrate, picks up color of metal ==> metalness factor m varies from 0 to 1, applies to color of highlight.
        -> on plastics, the light bounces off a surface layer, and keeps more of its own color composition (metalness factor m=0).

Surface Characterization.

NOTE: The notations and conventions used in different books vary. What we use in this course is slightly richer than what Shirley describes in Chapter 9.

Brightness Normalization.

Normally one tries to carefully choose lights so that the produced brightnesses fall into the range 0 to 1.0,
which is then mapped onto the, say, 256 discrete beam intensities in the CRT.
In spite of best intentions the sum of all calculated brightnesses may exceed unity; this may produce strange effects if left unchecked !
--> at the very least: clip to unity
--> better: detect this, and scale down all brightness values on object or in whole scene.

Now that we know what the brightness is that we would like to represent,
the question arises, how can we efficiently generate all the pixels of the right brightness ?

For Ray-Tracing we just need to know the above surface properties, the normal direction of the surface, and the direction to the various light sources.

Reading Assignments:

Skim: ( to get a first idea of what will be discussed in the future, try to remember the grand ideas, but no need to worry about the details):
Shirley, 2nd Ed: Chapters 9-10.

Study: ( i.e., try to understand fully, so that you can answer questions on an exam):
Shirley, 2nd Ed: Ch 9.1-9.2; Ch 10.1-10.4.

Programming Assignment 2:

Assignments are typically worth 12 points + a max of 2 extra credits. ==> Accounting swill be done separately!
Assignment #3 is due (electronically submitted) before Thursday 2/19, 11:00pm. <== THIS ASSIGNMENT CAN BE DONE IN PAIRS !
Assignment #4: will be done individually again; is due (electronically submitted) before Thursday 2/26, 11:00pm.

PREVIOUS < - - - - > CS 184 HOME < - - - - > CURRENT < - - - - > NEXT

Page Editor: Carlo H. Séquin