Subsections

• Memory-based Reinforcement Learning of Hidden-state Control Policies
• Variable-K Nearest Neighbor Algorithm

Finding optimal action- selection policies

Given a POMDP problem, one wishes to construct a policy, $\pi$which maps a function on observations to actions, and whose execution leads to maximizing the criterion function in Equation (1). Methods for constructing a policy based on a POMDP model can be divided into two approaches: indirect and direct. Indirect methods attempt to estimate the actual state of the world, and then treat the problem as a conventional Markov Decision problem (MDP) with full state access. Direct methods forgo recovery of the actual state and attempt to characterize optimal behavior given only actions and observations. We will discuss examples of each of these, and then a hybrid approach using memory-based approaches to model world state.

Indirect methods combine a predictive forward model that recovers an estimate of absolute state with a conventional MDP learning method. Given absolute state, recovering an optimal policy for a MDP is a well-studied problem. Q-Learning is one widely used reinforcement learning method for finding an optimal MDP policy. The Q function maps state and action pairs to a utility value, which is the expected discounted future reward given that state and action. Optimal utility values can be computed on-line using a Temporal Differences method [25], which is an incremental form of a full Dynamic Programming approach [5]. In the case of deterministic state transitions, to maximize Eq. (1) the optimal Q function must satisfy 

$$Q(s,a) = r + \gamma\max_{a\in{\cal A}}Q(s',a)$$ (2)

where s' is the next state after executing action a in state s. To find an optimal Q, the difference between the two sides of Eq. (2) is minimized, using the well known update rule: 

$$Q(s,a) \leftarrow (1-\beta)Q(s,a) + \beta(r + \gamma\max_{a\in{\cal A}}Q(s',a)) ,$$ (3)

where $\beta$ is the learning rate parameter. This has been shown to converge to optimal policies when the environment is Markovian and the Q-function is represented literally as a lookup table [26].

Several approaches have been proposed which combine a predictive model to transform a POMDP to a MDP and then use Q-learning to construct a policy function. The Perceptual Distinctions Approach (PDA) developed by Chrisman [8] uses a state-splitting approach to construct a model of the domain. A modified Expectation-Minimization algorithm was used to alternate between maximizing the model probability given a fixed number of internal states, and splitting perceptually aliased states into new states. A similar method was developed by McCallum, the Utile Distinction Memory approach (UDM), which split states based on the predicted reward [19]. Given a state estimator learned via PDA or UDM, or simply computed from T and O, an optimal policy can be constructed [7]. However these indirect methods have been criticized as being computationally intractable in realistic environments [14]. Indeed, the empirical results suggest that a prohibitive amount of training time is required with these algorithms [20].

Rather than convert a POMDP to a MDP through state estimation, direct methods update a value function over observations without recovering absolute state. Jaakkola et. al. present a Monte-Carlo algorithm for policy evaluation and improvement using Q-values defined over actions and observations [14]. They provide a recursive formulation of the Monte-Carlo algorithm, and prove the policy improvement method will converge to at least a local maximum.

A hybrid approach sharing both direct and indirect qualities has been explored by Lin [16] and McCallum [20]. These methods use a memory-based approach to identifying state. Lin's window-Q algorithm supplies a history of the N most recent observations and actions to a conventional Q-learning algorithm. The intuition is that perceptually aliased states can be discriminated by indexing utility over a vector of recent experience. A significant drawback to this approach is the use of fixed window size. McCallum's Instance-Based state identification method extends this approach to use windows of varying length, using a sequence matching criterion with a K-nearest neighbor utility representation.

The memory-based approach to hidden-state reinforcement learning can be successfully applied to our AGR task, once we generalize the the nearest-neighbor algorithm. As described in Section 3.2, we modify the nearest neighbor computation to pool all experience whose similarity (e.g., sequence match length) is approximately equal to the K'-th percentile rank, rather than simply using the K largest similarity scores. This is important in domains where the world is non-stationary, such as with rapidly changing target and distractor patterns; in this case we need to average all experiences with a particular sequence of observations when computing utility. We first describe the basic memory-based, hidden-state reinforcement learning algorithm, and then present our extensions.

Memory-based Reinforcement Learning of Hidden-state Control Policies

Instance-based Q-learning replaces the state-action table with a distributed utility representation [20]. Given a history of action, reward, and observation tuples, (a[t],r[t],o[t]), $0\leqt\leq T$, a Q-value is also stored with each time-step, q[t]. Utility is computed by averaging Q-values of the most similar previous experiences, defined using a sequence match criterion. Q-values are computed, and the Q-learning update rule applied, maintaining this distributed, memory-based representation.

If full access to the state were available and a table were used to represent Q values, this would simply be a table look-up  operation, but we do not have full access to the state, nor are we using a table representation.  Instead, utility is associated with the implicit state that the system was in at the previous time point.  Using McCallum's Nearest Sequence Memory (NSM) algorithm, we find the $K$ nearest neighbors in the history list for a given action, and compute their average Q value.

Nearest neighbors are computed using a sequence match criterion; we look to prior experiences that are most similar to the current time point, in terms of having had the same preceding sequence of actions and observations. For each element on the history list, we compute the sequence match criterion with the current time point, M(i,T), where M(i,j) indicates the number of action and observations that overlap between the sequence ending at time i and the sequence ending at time j: 

$$M(i,j) = S(i,j) + M(i-1,j-1) ~~{\rm if}~ S(i,j)\gt$$ (4)

$$~~~~~ 0 \quad {\rm otherwise} ~.$$ We modify McCallum's algorithm slightly and ignore reward in computing matches: we define S(i,j) to be 1 if o[i]=o[j] or a[i]=a[j], 2 if both are equal, and otherwise; we also define S(i,j)=0 if the low-resolution component of o[i] and o[j] both indicate an empty field.

For each candidate action, we compute the K most similar previous experiences that were then followed by the candidate action. Using a superscript in parentheses to denote the action index of a Q-value, we then compute 

$$Q^{(a^*)}[T] = (1/K)\sum_{i=0}^T v^{(a^*)}[i]q[i] ~,$$ (5)

where v^(a*)[i] indicates whether the history tuple at time-step i votes when computing the Q-value of a new action a^*: v^(a*)[i] is set to 1 when a[i]=a^* and M(i-1,T) is among the K largest match values for all k which have a[k] = a^*, otherwise it is set to .

Given Q values for each action the optimal policy is simply 

$$\pi[T] = \arg \max_{a^* \in \cal A} Q^{(a^*)}[T] ~.$$ (6)

The new action a[T+1] is chosen either according to this policy or based on an exploration strategy; a random action is taken whenever maximum utility is zero. In either case, the action is executed yielding an observation and reward, and a new tuple added to the history. The new Q-value is set to be the Q value of the chosen action, q[T+1]=Q^(a[T+1])[T]. The update step of Q learning is then computed, evaluating 

$$U[T+1] = \max_{a^* \in \cal A} Q^{(a^*)}[T+1] ~,$$ (7)

$$q[i] \leftarrow (1-\beta )q[i] + \beta (r[i] + \gamma U[T+1]) ~,$$ (8)

for each i such that v^(a[T+1])[i] = 1.

Variable-K Nearest Neighbor Algorithm

  The key to successful application of instance-based Q-learning algorithm is the identification of the appropriate instances (e.g. memories) on which to base estimates of the utility of a particular new action. In our AGR task, it is especially important that the utility of a particular action given a particular observation history be estimated from previous experience on both target and distractor trials. Estimates of utility which are based only trials with the target present will greatly overestimate the utility of all actions, since with the target present by definition any action chain followed by accept will yield positive reward. Conversely, estimates of utility based only on trials with distractors will grossly underestimate the true utility. Effective learning occurs in our system only when the utility of a particular action is considered over trials with both target and distractor.

This poses a problem for the instance-based algorithm defined above, which finds voting instances using a strict K-nearest neighbor method, since it depends critically on choosing the correct value of K. A value which is too small will miss some relevant experience, and yield an unreliable utility estimate; a value which is too large will merge together instances which are actually different states, returning us to the problem of perceptual aliasing. Since the number of instances (memories) which are relevant to a particular utility estimate may vary greatly depending on the distribution of target and distractor trials, no fixed value of K will suffice.

A simple example illustrates the problem: consider the estimation of the utility of accept when the previous observation/action sequence was to foveate the face and observe a neutral expression. Assume that the target and all distractors all have a face with neutral expression, so this should be of no use in discriminating target from distractor. During the training phase the system will likely have explored this sequence several times, some with the target and some with the distractor. When match similarities are computed, the memories with maximum match value will indeed all correspond to the relevant previous experience. There may be 20 such previous experiences, but a strict K-nearest neighbor algorithm with K=4 will ignore 16 of them. If these 4 memories happen to miss experiences with the target, which is not unlikely, then the computed utility will be incorrect.

Rather than set K very large and risk merging truly different states, we instead propose a new algorithm, which we call Variable-K Nearest Neighbors. Variable-K differs from Strict-K in that all memories with a given match length are included in the voting set, e.g., are pooled together when estimating utility.

In the Variable-K algorithm, we assert a minimum percentage kp of experience to be included. (If there is no noise in the match function, this can be effectively set to zero; in our experiments we used $kp=5\%$) We histogram the match lengths of all memories, and sort them from largest to smallest. We then find the match length value m' such that the $kp\%$ of memories have larger match lengths than m'. We then subtract a fixed amount kt to this match length value, and include all memories with match value greater than m'-kt into the voting set.

The effect of this algorithm is to find a percentage of nearest neighbors with largest match values, as does strict-K, but then to include all other memories with roughly the same match length. In the above example, all 20 experiences would be included in the voting set, and utility accurately estimated. In practice we have used kt=1, and found this algorithm greatly improved the performance of instance based Q-learning given the multiple trial (e.g. non-stationary world) structure of our AGR task.
 
 

Figure 2: AGR results for simple imagery targets: (a) set of four target patterns, where the first and last pair are indistinguishable at low-resolution (b) recognition performance (percentage of correct trials) for varying amounts of observation noise. 

(a)

(b)

With the Variable-K enhancement, instance-based Q-learning can find optimal policies to solve AGR tasks. Figure 2 shows the results using this hidden-state Q-learning algorithm on an AGR task using image-based world state. In this example four different world states were used for the target and distractors; varying amounts of noise were added to the actual observations at run-time. We ran the system by randomly selecting one of the patterns as target, and using the other three as distractors. This Q-learning system easily learns the correct foveation policies to actively recognize these targets; e.g., to foveate down to recognize one of the square targets, and to foveate up to recognize one of the circle targets. For moderate levels of noise, each pattern can be easily discriminated from all the others, however, as $\sigma$ exceeds 20.0, the high-resolution information in the signal becomes insufficient to discriminate the two square targets and the two circle target, so performance drops by half. As $\sigma$ approaches 60.0, the low-resolution information becomes indistinguishable, and all the targets are confused, leading to a recognition rate of zero.

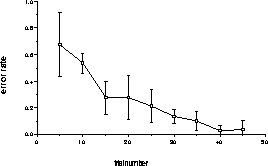
Successful policies were also found for the interactive interface domain. Figure 3 shows the recognition performance on the set of gestures shown in Figure 1(c,d). These patterns were quite simple; and convergence to an accurate recognition policy is straightforward. For more complicated targets, it is possible for the random policy search to converge prematurely to a local maxima of Equation (1), which can correspond to good performance but still have errors. While there are many strategies for focusing search in a structured manner and overcoming local minima, we have implemented a simple strategy: we detect local minima and restart the learning process with a new random seed when premature convergence is found. We detect convergence by examining average recognition error over a window of (N_c=100) recent of trials: if during the entire window average the error rate has remained fixed, was above an upper threshold ($99\%$) or below a lower threshold ($1\%$), we declare the algorithm converged. We then test N_c subsequent trials; if an error is detected we determine that this was a local minima, and restart the learning process, clearing experience memory and beginning again with a new random seed (which affects both the sequence of target/distractor patterns and the exploration actions chosen.) Additionally if we exceed a fixed maximum memory length (M_l=10000), we restart learning. This algorithm is suboptimal in terms of learning time, but does find correct recognition policy solutions. In the following section we address the issue of how to extract a more efficient run-time representation from these learned policies.
 
 

Figure 3:  Performance with random exploration on AGR task with targets shown in Figure 1(c,d). For each run, one gesture was randomly chosen as target, and the other three used as distractors. Results were averaged over 100 runs; average error rate is plotted as a function of trial number during each run. Recognition converges to correct performance on average after approximately 40 trials.

9/14/1998