Inverse Kinematics, Formal Approach

Let's assume we have an articulated skelton arm with several links.
The arm is fixed in space at its root end.
The task is to get the end effector in a predescribed place

A More Formal Approach:

Define an error metric E that tells us how much the current state falls short of the goal state.
(Example:  Euclidean distance between end effector and target location).

Compute the  Jacobian  of this error with respect to all "inputs" (parameter values at joints).

Apply Newton's method or some other procedure to coax the error towards zero.

ITERATE !  (This requires re-computing the Jacobian after every step).

The Jacobian is the multidimensional extension to differentiation of a single variable.

In this context it tells us how points of interest in our system (typically some end effectors)
move as a function of some small changes to all the variables that define the state of the system.

Given the function:    E = f(q), 
where E is of dimension n (e.g., the dimension of space), and q is of dimension m (e.g., the DoF's of the linkage),
the Jacobian  J  is then the  n by m  matrix  of partial derivatives,
where the (i,j)th element of  J  is given by:   J_ij =df_i /dq_j
It computes differential changes in E, expressed as dE,  in terms of differential changes of q, expressed as dq : 

dE = J(q) dq.

The Jacobian can be calculated in closed form if the function f is simple enough.
In intractable cases we can use finite differences.

So now to find the state vector  that makes the error E go to zero,
we "just need to invert the last equation" that we started from:       q= f^-1(E).

But for all but the simplest articulated structures, the function f(q) is highly non-linear
and becomes rather complex as the number of links and DoFs increases;
and the inversion of this function becomes quickly impossible to perform analytically.

However, the problem can still be linearized, if we take small steps from the current state.
This requires inversion of the Jacobian:      dq= J^-1(dE);      
dq  now is the vector of the (small) changes that need to be made to the state vector to reduce the error by dE.

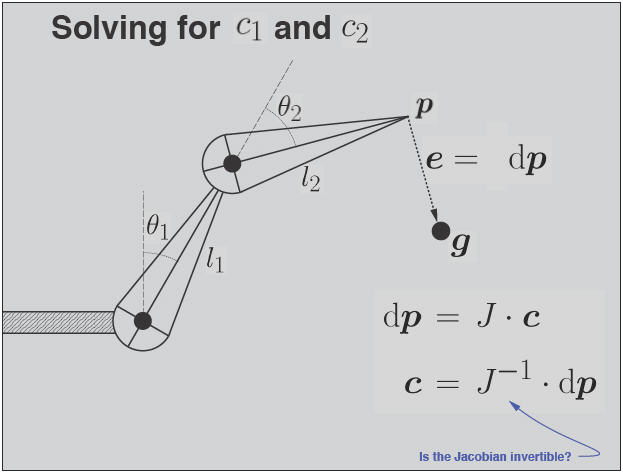
But the Jacobian itself may not invertible (e.g., if it is not square).  The problem may be over- or under-constrained.

==> Take a pseudo-inverse:
Using SVD:  J = Q S P^T   ==> inverse ==>  J^-1 = P S^-1 Q^T     but some diagonal values = 0 !    Just set   1/0  to  0.0

We still need to be careful about choosing a proper step size! 
Watch the errors; if they get too big, cut step size in half.

For more details, study:
Numerical Methods for Inverse Kinematics, by Niels Joubert, UC Berkeley, written for CS184.