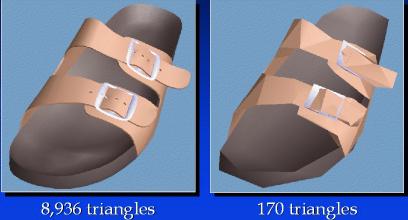
Noteworthy Papers on Meshing and Triangulation
(Your presentation is 10% of your final grade)

|
CS 294-74: Meshes and Geometry (Spring 2012)
Noteworthy Papers on Meshing and Triangulation (Your presentation is 10% of your final grade) |
Please have a date assigned to you no later than February 27. You are welcome to choose only a date now, and put off choosing the paper (or change your choice) until two weeks before your date. However, papers are assigned first-come first-served. You are also welcome to choose a relevant paper not on this list (and you are encouraged to do so if it is helpful to your own research), but please provide me with a copy two weeks before your presentation.
There is time for two student presentations on each available date. When a student chooses a date and paper, I'll put their name next to each below, so that you'll know which dates and papers were already taken last time I updated this page.
You must make an appointment with me to give a practice talk at least one week before your in-class talk, so that I have an opportunity to suggest improvements. (Note that I usually don't come to campus on Tuesdays.) Also see my advice on Giving an Academic Talk.
Your presentation should take 25 to 40 minutes. Don't feel you must present everything in a paper; rather, concentrate on presenting the most interesting or important parts. Give theoretical proofs only if you think you can present them well in the time allotted.
You may use a laptop or, if you dare, the whiteboard. Many of the authors have posted their own talk slides to the web, or will send them to you if you ask them. You are encouraged to use them as a source of figures, but you should make your own slides—don't try to give someone else's talk.
Wednesday, April 4 —
Anand Kulkarni, Brian Van Straalen.
Wednesday, April 11 —
Ethan Van Andel, Pardeep Kumar.
Wednesday, April 18 —
Allen Xiao, Ricardo Garcia.
Monday, April 23 —
Sushrut Pavanaskar.
Wednesday, April 25 —
Eric Turner, Laura Devendorf.
Wednesday, May 2 —
Peter Cottle, Youngwook Kwon.
 Marshall Bern, Scott Mitchell, and Jim Ruppert,
Linear-Size Nonobtuse Triangulation of Polygons,
Discrete & Computational Geometry 14:411–428, 1995.
Gnuzipped PostScript (93k) or
PDF (280k).
How to triangulate a polygon so that no angle is larger than 90o.
(There is no bound on the smallest angle.)
For a brief description of this result,
see Bern and Eppstein, pages 29–30.
There is also a version of this algorithm that creates quadrilateral meshes
(further down this page).
Marshall Bern, Scott Mitchell, and Jim Ruppert,
Linear-Size Nonobtuse Triangulation of Polygons,
Discrete & Computational Geometry 14:411–428, 1995.
Gnuzipped PostScript (93k) or
PDF (280k).
How to triangulate a polygon so that no angle is larger than 90o.
(There is no bound on the smallest angle.)
For a brief description of this result,
see Bern and Eppstein, pages 29–30.
There is also a version of this algorithm that creates quadrilateral meshes
(further down this page).
 Matthew T. Dickerson, J. Mark Keil, and Mark H. Montague,
A Large Subgraph of the Minimum Weight Triangulation,
Discrete & Computational Geometry 18(3):289–304, October 1997.
PDF (214k).
The minimum weight triangulation (MWT) is the triangulation of a point set
whose total edge length is shortest.
For many years, it was not known whether there is a polynomial algorithm for
the MWT. Recently, the problem was proven to be NP-hard;
but for most point sets of modest size,
the MWT can be computed by techniques discussed here.
Incidentally, the cubic-time algorithm this paper mentions for finding the MWT
of a polygon (rather than a point set, which is NP-complete)
is Klincsek's algorithm (see Bern and Eppstein, pages 17–18).
Matthew T. Dickerson, J. Mark Keil, and Mark H. Montague,
A Large Subgraph of the Minimum Weight Triangulation,
Discrete & Computational Geometry 18(3):289–304, October 1997.
PDF (214k).
The minimum weight triangulation (MWT) is the triangulation of a point set
whose total edge length is shortest.
For many years, it was not known whether there is a polynomial algorithm for
the MWT. Recently, the problem was proven to be NP-hard;
but for most point sets of modest size,
the MWT can be computed by techniques discussed here.
Incidentally, the cubic-time algorithm this paper mentions for finding the MWT
of a polygon (rather than a point set, which is NP-complete)
is Klincsek's algorithm (see Bern and Eppstein, pages 17–18).
I have an accompanying video (on videotape):
Patrice Belleville, Mark Keil, Michael McAllister, and Jack Snoeyink,
On Computing Edges That Are In All Minimum-Weight Triangulations,
Fifth Annual Video Review of Computational Geometry, ACM, May 1996.
See also
Proceedings of the Twelfth Annual Symposium on Computation Geometry
(Pittsburgh, Pennsylvania), pages V7–V8, ACM, May 1996.
 Steven Pav and Noel Walkington,
Delaunay Refinement by Corner Lopping,
14th International Meshing Roundtable (San Diego, California),
pages 165–181, September 2005.
PDF (1,373k).
Many real-world domains have curved boundaries.
This paper extends Ruppert's algorithm to deal with curves.
(Unfortunately, the electronic version of this paper is missing two figures.
Ask me for photocopies.)
Steven Pav and Noel Walkington,
Delaunay Refinement by Corner Lopping,
14th International Meshing Roundtable (San Diego, California),
pages 165–181, September 2005.
PDF (1,373k).
Many real-world domains have curved boundaries.
This paper extends Ruppert's algorithm to deal with curves.
(Unfortunately, the electronic version of this paper is missing two figures.
Ask me for photocopies.)
 Hale Erten and Alper Üngör,
Triangulations with Locally Optimal Steiner Points,
Symposium on Geometry Processing 2007 (Barcelona, Spain),
pages 143–152, July 2007.
PDF (615k).
This paper modifies Ruppert's algorithm by inserting new vertices
not just at triangle circumcircles, but at locations that are less likely
to create new bad triangles.
The meshes Erten and Üngör generate have fewer triangles
than Ruppert's meshes (for a fixed bound on the minimum angle),
or can be refined until their worst angles are about 42o
(in practice—there's no guarantee).
Allen Xiao.
Hale Erten and Alper Üngör,
Triangulations with Locally Optimal Steiner Points,
Symposium on Geometry Processing 2007 (Barcelona, Spain),
pages 143–152, July 2007.
PDF (615k).
This paper modifies Ruppert's algorithm by inserting new vertices
not just at triangle circumcircles, but at locations that are less likely
to create new bad triangles.
The meshes Erten and Üngör generate have fewer triangles
than Ruppert's meshes (for a fixed bound on the minimum angle),
or can be refined until their worst angles are about 42o
(in practice—there's no guarantee).
Allen Xiao.
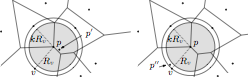 Benoît Hudson, Gary Miller, and Todd Phillips,
Sparse Voronoi Refinement,
15th International Meshing Roundtable (Birmingham, Alabama),
pages 339–356, September 2006.
PDF (226k).
In three dimensions, the Delaunay triangulation of n points may
have Θ(n2) tetrahedra.
If you run Delaunay refinement on such a domain, the new vertices will
eventually bring the complexity down to something reasonable;
but meanwhile you will suffer a quadratic hit in your running time.
Sparse Voronoi refinement guarantees a near-optimal running time by
interleaving refinement with insertion of the input vertices
(rather than constructing a Delaunay triangulation of the input before
beginning to refine).
Benoît Hudson, Gary Miller, and Todd Phillips,
Sparse Voronoi Refinement,
15th International Meshing Roundtable (Birmingham, Alabama),
pages 339–356, September 2006.
PDF (226k).
In three dimensions, the Delaunay triangulation of n points may
have Θ(n2) tetrahedra.
If you run Delaunay refinement on such a domain, the new vertices will
eventually bring the complexity down to something reasonable;
but meanwhile you will suffer a quadratic hit in your running time.
Sparse Voronoi refinement guarantees a near-optimal running time by
interleaving refinement with insertion of the input vertices
(rather than constructing a Delaunay triangulation of the input before
beginning to refine).
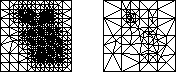 Marshall Bern, David Eppstein, and John R. Gilbert,
Provably Good Mesh Generation,
Journal of Computer and System Sciences
48(3):384–409, June 1994.
Gnuzipped PostScript (151k) or
PDF (341k).
This classic paper gives the first size-optimal guaranteed-quality
meshing algorithm (from before Ruppert invented his algorithm).
It's based on quadtrees.
For a brief description of this result,
see Bern and Eppstein, pages 22–25.
Marshall Bern, David Eppstein, and John R. Gilbert,
Provably Good Mesh Generation,
Journal of Computer and System Sciences
48(3):384–409, June 1994.
Gnuzipped PostScript (151k) or
PDF (341k).
This classic paper gives the first size-optimal guaranteed-quality
meshing algorithm (from before Ruppert invented his algorithm).
It's based on quadtrees.
For a brief description of this result,
see Bern and Eppstein, pages 22–25.
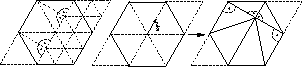 Friedhelm Neugebauer and Ralf Diekmann,
Improved Mesh Generation: Not Simple But Good,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 257–270, October 1996.
Gnuzipped PostScript (84k) or
PDF (251k).
An improvement to the Bern, Eppstein, and Gilbert algorithm
that uses a rhomboidal quadtree.
Friedhelm Neugebauer and Ralf Diekmann,
Improved Mesh Generation: Not Simple But Good,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 257–270, October 1996.
Gnuzipped PostScript (84k) or
PDF (251k).
An improvement to the Bern, Eppstein, and Gilbert algorithm
that uses a rhomboidal quadtree.
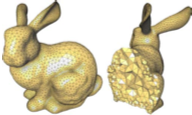 Pierre Alliez, David Cohen-Steiner, Mariette Yvinec, and Mathieu Desbrun,
Variational Tetrahedral Meshing,
ACM Transactions on Graphics 24(3):617–625, 2005.
Special issue on Proceedings of SIGGRAPH 2005.
PDF (778k).
An example of tetrahedral mesh generation from the graphics literature.
Their algorithm iterates between a smoothing operation that
minimizes a function (the volume between the lifted triangulation
on the parabolic lifting map and the paraboloid itself) and recomputing
the Delaunay triangulation (which minimizes the same function).
In other words, it alternates between moving the vertices and
changing their connectivity.
The authors seem to get good meshes in practice, with few slivers
(though they do not report the worst tetrahedra; instead they report
distributions of quality).
Warning: I know two people who have independently implemented this algorithm,
and both report that recovering good sliver-free boundaries is much harder
than the authors indicate.
Pierre Alliez, David Cohen-Steiner, Mariette Yvinec, and Mathieu Desbrun,
Variational Tetrahedral Meshing,
ACM Transactions on Graphics 24(3):617–625, 2005.
Special issue on Proceedings of SIGGRAPH 2005.
PDF (778k).
An example of tetrahedral mesh generation from the graphics literature.
Their algorithm iterates between a smoothing operation that
minimizes a function (the volume between the lifted triangulation
on the parabolic lifting map and the paraboloid itself) and recomputing
the Delaunay triangulation (which minimizes the same function).
In other words, it alternates between moving the vertices and
changing their connectivity.
The authors seem to get good meshes in practice, with few slivers
(though they do not report the worst tetrahedra; instead they report
distributions of quality).
Warning: I know two people who have independently implemented this algorithm,
and both report that recovering good sliver-free boundaries is much harder
than the authors indicate.
 Siu-Wing Cheng, Tamal Krishna Dey, Herbert Edelsbrunner, Michael A. Facello,
and Shang-Hua Teng, Sliver Exudation,
Journal of the ACM 47(5):883–904, September 2000.
Gnuzipped PostScript (120k) or
PDF (294k).
If you present this paper, I suggest you include figures and results from
Herbert Edelsbrunner and Damrong Guoy,
An Experimental Study of Sliver Exudation,
Engineering with Computers 18:229–240, 2002.
PDF (790k).
A provably good mesh improvement algorithm that uses flips
to remove slivers from a Delaunay mesh.
The algorithm keeps the triangulation weighted Delaunay at all times.
Unfortunately, the provable bounds are so weak (probably less than
a millionth of a degree for the dihedral angles) that the authors don't bother
to compute them; but Edelsbrunner and Guoy show that the algorithm is
much better in practice than the theory can guarantee
(though not as good as Freitag and Ollivier-Gooch's heuristic approach).
Anand Kulkarni.
Siu-Wing Cheng, Tamal Krishna Dey, Herbert Edelsbrunner, Michael A. Facello,
and Shang-Hua Teng, Sliver Exudation,
Journal of the ACM 47(5):883–904, September 2000.
Gnuzipped PostScript (120k) or
PDF (294k).
If you present this paper, I suggest you include figures and results from
Herbert Edelsbrunner and Damrong Guoy,
An Experimental Study of Sliver Exudation,
Engineering with Computers 18:229–240, 2002.
PDF (790k).
A provably good mesh improvement algorithm that uses flips
to remove slivers from a Delaunay mesh.
The algorithm keeps the triangulation weighted Delaunay at all times.
Unfortunately, the provable bounds are so weak (probably less than
a millionth of a degree for the dihedral angles) that the authors don't bother
to compute them; but Edelsbrunner and Guoy show that the algorithm is
much better in practice than the theory can guarantee
(though not as good as Freitag and Ollivier-Gooch's heuristic approach).
Anand Kulkarni.
 Marshall Bern and David Eppstein,
Quadrilateral Meshing by Circle Packing,
Sixth International Meshing Roundtable (Park City, Utah),
pages 7–19, October 1997.
Gnuzipped PostScript (267k) or
PDF (139k).
An elegant algorithm for creating quadrilateral meshes with no angles larger
than 120o.
(There is no bound on the smallest angle.)
Marshall Bern and David Eppstein,
Quadrilateral Meshing by Circle Packing,
Sixth International Meshing Roundtable (Park City, Utah),
pages 7–19, October 1997.
Gnuzipped PostScript (267k) or
PDF (139k).
An elegant algorithm for creating quadrilateral meshes with no angles larger
than 120o.
(There is no bound on the smallest angle.)
 Paul Kinney,
CleanUp: Improving Quadrilateral Finite Element Meshes,
Sixth International Meshing Roundtable (Park City, Utah),
pages 449–461, October 1997.
Gnuzipped PostScript (40k) or
PDF (36k).
How to apply topological transformations to improve an existing
quadrilateral mesh.
Paul Kinney,
CleanUp: Improving Quadrilateral Finite Element Meshes,
Sixth International Meshing Roundtable (Park City, Utah),
pages 449–461, October 1997.
Gnuzipped PostScript (40k) or
PDF (36k).
How to apply topological transformations to improve an existing
quadrilateral mesh.
 Kenji Shimada, Jia-Huei Liao, and Takayuki Itoh,
Quadrilateral Meshing with Directionality Control through the
Packing of Square Cells,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 61–75, October 1998.
Gnuzipped PostScript (627k) or
PDF (723k).
Bubble meshing for quadrilateral meshes.
Whereas the iterative nature of bubble meshing makes it uncompetitively slow
for (isotropic) triangular meshing, it's much more attractive for
the tougher problem of quadrilateral meshing.
Kenji Shimada, Jia-Huei Liao, and Takayuki Itoh,
Quadrilateral Meshing with Directionality Control through the
Packing of Square Cells,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 61–75, October 1998.
Gnuzipped PostScript (627k) or
PDF (723k).
Bubble meshing for quadrilateral meshes.
Whereas the iterative nature of bubble meshing makes it uncompetitively slow
for (isotropic) triangular meshing, it's much more attractive for
the tougher problem of quadrilateral meshing.
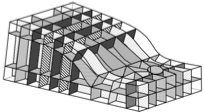 Matthew L. Staten, Steven J. Owen, and Ted D. Blacker,
Unconstrained Paving & Plastering: Progress Update,
15th International Meshing Roundtable (Birmingham, Alabama),
pages 469–486, September 2006.
PDF (3,647k).
For additional details and pictures, you might also want to look at their
earlier installment,
Matthew L. Staten, Steven J. Owen, and Ted D. Blacker,
Unconstrained Paving & Plastering: A New Idea for All Hexahedral
Mesh Generation,
14th International Meshing Roundtable (San Diego, California),
pages 399–416, September 2005.
PDF (2,176k).
Plastering is an advancing-front method for hexahedral mesh generation,
and the three-dimensional equivalent of paving.
Unstructured hexahedral mesh generation is an extremely hard problem.
Although it is far from completely solved, this paper will give you a sense
of the state of the art and why the problem is so hard.
Matthew L. Staten, Steven J. Owen, and Ted D. Blacker,
Unconstrained Paving & Plastering: Progress Update,
15th International Meshing Roundtable (Birmingham, Alabama),
pages 469–486, September 2006.
PDF (3,647k).
For additional details and pictures, you might also want to look at their
earlier installment,
Matthew L. Staten, Steven J. Owen, and Ted D. Blacker,
Unconstrained Paving & Plastering: A New Idea for All Hexahedral
Mesh Generation,
14th International Meshing Roundtable (San Diego, California),
pages 399–416, September 2005.
PDF (2,176k).
Plastering is an advancing-front method for hexahedral mesh generation,
and the three-dimensional equivalent of paving.
Unstructured hexahedral mesh generation is an extremely hard problem.
Although it is far from completely solved, this paper will give you a sense
of the state of the art and why the problem is so hard.
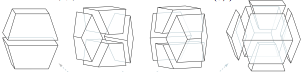 Marshall Bern, David Eppstein, and Jeff Erickson,
Flipping Cubical Meshes,
Engineering with Computers 18(3):173–187, October 2002.
PDF (218k).
This paper describes flips that replace one set of hexahedral elements
with another set, and likewise for quadrilateral flips.
It also has a discussion (mainly of theoretical interest) of the circumstances
under which you can guarantee that a flip will create hexahedra with planar
faces.
Marshall Bern, David Eppstein, and Jeff Erickson,
Flipping Cubical Meshes,
Engineering with Computers 18(3):173–187, October 2002.
PDF (218k).
This paper describes flips that replace one set of hexahedral elements
with another set, and likewise for quadrilateral flips.
It also has a discussion (mainly of theoretical interest) of the circumstances
under which you can guarantee that a flip will create hexahedra with planar
faces.
 Ted Blacker,
The Cooper Tool,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 13–29, October 1996.
Gnuzipped PostScript (1,236k) or
PDF (1,895k).
The most common technique for generating a hexahedral mesh is sweeping
a quadrilateral mesh along the third axis.
This technique only works well if the object being meshed is nicely structured.
Here's a relatively sophisticated discussion of how to make sweeping work
on complicated shapes.
Ted Blacker,
The Cooper Tool,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 13–29, October 1996.
Gnuzipped PostScript (1,236k) or
PDF (1,895k).
The most common technique for generating a hexahedral mesh is sweeping
a quadrilateral mesh along the third axis.
This technique only works well if the object being meshed is nicely structured.
Here's a relatively sophisticated discussion of how to make sweeping work
on complicated shapes.
 Robert W. Leland, Darryl J. Melander, Ray W. Meyers, Scott A. Mitchell,
and Timothy J. Tautges,
The Geode Algorithm: Combining Hex/Tet Plastering,
Dicing and Transition Elements
for Automatic, All-Hex Mesh Generation,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 515–521, October 1998.
Gnuzipped PostScript (206k) or
PDF (203k).
An interesting real-world paper that gives you an idea what kinds of
clever tricks and compromises people make
when they write industrial meshing software.
Robert W. Leland, Darryl J. Melander, Ray W. Meyers, Scott A. Mitchell,
and Timothy J. Tautges,
The Geode Algorithm: Combining Hex/Tet Plastering,
Dicing and Transition Elements
for Automatic, All-Hex Mesh Generation,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 515–521, October 1998.
Gnuzipped PostScript (206k) or
PDF (203k).
An interesting real-world paper that gives you an idea what kinds of
clever tricks and compromises people make
when they write industrial meshing software.
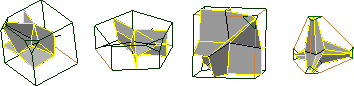 Alla Sheffer, Michal Etzion, Ari Rappoport, and Michel Bercovier,
Hexahedral Mesh Generation using the Embedded Voronoi Graph,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 347–364, October 1998.
Gnuzipped PostScript (2,155k) or
PDF (2,972k).
The authors use a structure similar to the medial axis to decompose
a domain into polyhedra for which simple sweep algorithms can create
a hexahedral mesh.
Alla Sheffer, Michal Etzion, Ari Rappoport, and Michel Bercovier,
Hexahedral Mesh Generation using the Embedded Voronoi Graph,
Seventh International Meshing Roundtable (Dearborn, Michigan),
pages 347–364, October 1998.
Gnuzipped PostScript (2,155k) or
PDF (2,972k).
The authors use a structure similar to the medial axis to decompose
a domain into polyhedra for which simple sweep algorithms can create
a hexahedral mesh.
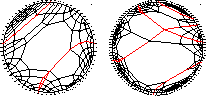 Timothy J. Tautges, Ted Blacker, and Scott Mitchell,
The Whisker Weaving Algorithm: A Connectivity-Based Method for Constructing
All-Hexahedral Finite Element Meshes.
Gnuzipped PostScript (155k) or
PDF (155k).
You might also find it useful to consult the more detailed description
of the spatial twist continuum in
Peter Murdoch, Steven Benzley, Ted Blacker, and Scott A. Mitchell,
The Spatial Twist Continuum Captures the Global Connectivity of an
All-Hexahedral Finite Element Mesh
Gnuzipped PostScript (33k) or
PDF (38k).
Whisker weaving is a topological approach to
unstructured hexahedral mesh generation of general shapes.
Although it has not yielded a practical mesh generation algorithm
(because it neglects geometry too much), these papers are still
a great introduction to the topological difficulties of hexahedral meshing,
and remain a must-read for anyone trying to understand the problem.
Ask me for a companion paper that describes the Spatial Twist Continuum (STC)
in greater detail; it has some helpful figures.
(In fact, you might wind up mostly just presenting the STC paper.)
Timothy J. Tautges, Ted Blacker, and Scott Mitchell,
The Whisker Weaving Algorithm: A Connectivity-Based Method for Constructing
All-Hexahedral Finite Element Meshes.
Gnuzipped PostScript (155k) or
PDF (155k).
You might also find it useful to consult the more detailed description
of the spatial twist continuum in
Peter Murdoch, Steven Benzley, Ted Blacker, and Scott A. Mitchell,
The Spatial Twist Continuum Captures the Global Connectivity of an
All-Hexahedral Finite Element Mesh
Gnuzipped PostScript (33k) or
PDF (38k).
Whisker weaving is a topological approach to
unstructured hexahedral mesh generation of general shapes.
Although it has not yielded a practical mesh generation algorithm
(because it neglects geometry too much), these papers are still
a great introduction to the topological difficulties of hexahedral meshing,
and remain a must-read for anyone trying to understand the problem.
Ask me for a companion paper that describes the Spatial Twist Continuum (STC)
in greater detail; it has some helpful figures.
(In fact, you might wind up mostly just presenting the STC paper.)
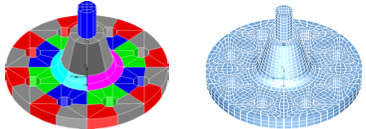 Matthias Müller-Hannemann,
Shelling Hexahedral Complexes for Mesh Generation,
Journal of Graph Algorithms and Applications 5(5):59–91, 2001.
PDF (736k).
Another topological approach to hexahedral mesh generation.
Müller-Hannemann avoids some of the problems that whisker weaving has
by first repairing the surface mesh to remove self-intersecting cycles in
the dual.
The volume mesh generation step works by performing transformations
that remove the remaining cycles from the surface mesh dual.
The hexahedra are determined by running this cycle-removal process in reverse.
Matthias Müller-Hannemann,
Shelling Hexahedral Complexes for Mesh Generation,
Journal of Graph Algorithms and Applications 5(5):59–91, 2001.
PDF (736k).
Another topological approach to hexahedral mesh generation.
Müller-Hannemann avoids some of the problems that whisker weaving has
by first repairing the surface mesh to remove self-intersecting cycles in
the dual.
The volume mesh generation step works by performing transformations
that remove the remaining cycles from the surface mesh dual.
The hexahedra are determined by running this cycle-removal process in reverse.
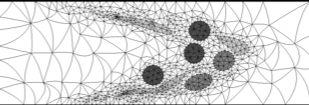 David Cardoze, Alexandre Cunha, Gary L. Miller, Todd Phillips, and
Noel Walkington,
A Bézier-Based Approach to Unstructured Moving Meshes,
Twentieth Annual Symposium on Computational Geometry (Brooklyn, New York),
pages 310–319, June 2004.
PDF (691k).
This paper uses Bézier triangular elements—elements
with curved edges, modeled by B-splines—and flips
to maintain a mesh that dynamically changes through time to model blood flow
(while maintaining the boundaries of the red blood cells).
The challenge is to keep the quality of the triangles good as they deform.
Ethan Van Andel.
David Cardoze, Alexandre Cunha, Gary L. Miller, Todd Phillips, and
Noel Walkington,
A Bézier-Based Approach to Unstructured Moving Meshes,
Twentieth Annual Symposium on Computational Geometry (Brooklyn, New York),
pages 310–319, June 2004.
PDF (691k).
This paper uses Bézier triangular elements—elements
with curved edges, modeled by B-splines—and flips
to maintain a mesh that dynamically changes through time to model blood flow
(while maintaining the boundaries of the red blood cells).
The challenge is to keep the quality of the triangles good as they deform.
Ethan Van Andel.
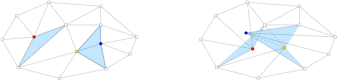 Pankaj K. Agarwal, Bardia Sadri, Hai Yu,
Untangling Triangulations through Local Explorations,
to appear in
Twenty-Fourth Annual Symposium on Computational Geometry
(College Park, Maryland), June 2008.
Draft PDF (242k).
When the vertices of a triangular mesh move during a Lagrangian finite element
simulation, some of the triangles may become inverted,
meaning that their orientations are reversed,
because there are folds in the fabric of the mesh.
In this circumstance, you cannot count on the flip algorithm to correct
the tangled mesh, so the authors instead locally retriangulate small portions
of the mesh.
Starting with one inverted seed triangle, this paper shows how
to find a minimal set of triangles (including the seed) that
can be removed and replaced solely by triangles that are not inverted.
Note that this is the submitted version (taken from Bardia Sadri's web page);
the final conference version is not available yet.
Pankaj K. Agarwal, Bardia Sadri, Hai Yu,
Untangling Triangulations through Local Explorations,
to appear in
Twenty-Fourth Annual Symposium on Computational Geometry
(College Park, Maryland), June 2008.
Draft PDF (242k).
When the vertices of a triangular mesh move during a Lagrangian finite element
simulation, some of the triangles may become inverted,
meaning that their orientations are reversed,
because there are folds in the fabric of the mesh.
In this circumstance, you cannot count on the flip algorithm to correct
the tangled mesh, so the authors instead locally retriangulate small portions
of the mesh.
Starting with one inverted seed triangle, this paper shows how
to find a minimal set of triangles (including the seed) that
can be removed and replaced solely by triangles that are not inverted.
Note that this is the submitted version (taken from Bardia Sadri's web page);
the final conference version is not available yet.
 Frank Bossen and Paul Heckbert,
A Pliant Method for Anisotropic Mesh Generation,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 63–74, October 1996.
Gnuzipped PostScript (572k) or
PDF (450k).
Slides from a related talk by Paul are also available in
Gnuzipped PostScript (313k) or
PDF (353k).
Some applications require meshes in which the elements are anisotropic,
meaning that they are deliberately skinny, because you can interpolate
a function with anisotropic curvature more accurately by using properly
aligned skinny triangles.
This paper uses an iterative particle-based method to distribute vertices
to create an anisotropic triangular mesh.
Although iterative methods are relatively slow (compared to Delaunay
or advancing front methods), their flexibility makes them easy to apply
to problems like anisotropy.
If you present this paper, consider reading the paper below as well.
Laura Devendorf.
Frank Bossen and Paul Heckbert,
A Pliant Method for Anisotropic Mesh Generation,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 63–74, October 1996.
Gnuzipped PostScript (572k) or
PDF (450k).
Slides from a related talk by Paul are also available in
Gnuzipped PostScript (313k) or
PDF (353k).
Some applications require meshes in which the elements are anisotropic,
meaning that they are deliberately skinny, because you can interpolate
a function with anisotropic curvature more accurately by using properly
aligned skinny triangles.
This paper uses an iterative particle-based method to distribute vertices
to create an anisotropic triangular mesh.
Although iterative methods are relatively slow (compared to Delaunay
or advancing front methods), their flexibility makes them easy to apply
to problems like anisotropy.
If you present this paper, consider reading the paper below as well.
Laura Devendorf.
 Kenji Shimada,
Anisotropic Triangular Meshing of Parametric Surfaces via
Close Packing of Ellipsoidal Bubbles,
Sixth International Meshing Roundtable (Park City, Utah),
pages 375–390, October 1997.
Gnuzipped PostScript (521k) or
PDF (629k).
Bubble meshing uses an iterative particle-based method to
distribute vertices.
See the comments for the paper above; they all apply here too.
If you present this paper, consider reading the paper above as well.
Kenji Shimada,
Anisotropic Triangular Meshing of Parametric Surfaces via
Close Packing of Ellipsoidal Bubbles,
Sixth International Meshing Roundtable (Park City, Utah),
pages 375–390, October 1997.
Gnuzipped PostScript (521k) or
PDF (629k).
Bubble meshing uses an iterative particle-based method to
distribute vertices.
See the comments for the paper above; they all apply here too.
If you present this paper, consider reading the paper above as well.
 François Labelle and Jonathan Richard Shewchuk,
Anisotropic Voronoi Diagrams and
Guaranteed-Quality Anisotropic Mesh Generation,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 191–200,
Association for Computing Machinery, June 2003.
PostScript (910k) or
PDF (284k).
Slides from a related
talk (PDF, 1,301k) are also available.
This paper puts anisotropic mesh generation on firm theoretical ground.
The skewed elements are generated by a provably good
Voronoi refinement algorithm
that incrementally updates an anisotropic Voronoi diagram,
wherein each site has its own distorted distance metric.
François Labelle and Jonathan Richard Shewchuk,
Anisotropic Voronoi Diagrams and
Guaranteed-Quality Anisotropic Mesh Generation,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 191–200,
Association for Computing Machinery, June 2003.
PostScript (910k) or
PDF (284k).
Slides from a related
talk (PDF, 1,301k) are also available.
This paper puts anisotropic mesh generation on firm theoretical ground.
The skewed elements are generated by a provably good
Voronoi refinement algorithm
that incrementally updates an anisotropic Voronoi diagram,
wherein each site has its own distorted distance metric.
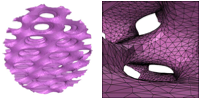 Jean-Daniel Boissonnat and Steve Oudot,
Provably Good Surface Sampling and Approximation,
Symposium on Geometry Processing (Aachen, Germany),
pages 9–18, June 2003.
PDF (technical report version, 1,728k).
This paper and
an earlier paper
by Paul Chew
created the foundations for provably good Delaunay mesh generation on surfaces.
If you present this paper, don't get lost in the details of the theorems;
focus on the high-level ideas.
Jean-Daniel Boissonnat and Steve Oudot,
Provably Good Surface Sampling and Approximation,
Symposium on Geometry Processing (Aachen, Germany),
pages 9–18, June 2003.
PDF (technical report version, 1,728k).
This paper and
an earlier paper
by Paul Chew
created the foundations for provably good Delaunay mesh generation on surfaces.
If you present this paper, don't get lost in the details of the theorems;
focus on the high-level ideas.
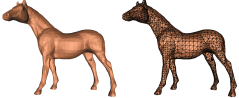 Scott Schaefer and Joe Warren,
Dual Marching Cubes: Primal Contouring of Dual Grids,
Computer Graphics Forum 24(2):195–201, 2005.
PDF (1,037k).
A clever isosurface extraction method that can often extract
thin features without using a fine grid.
It works in two steps.
The first step uses a dual octree method, similar to dual contouring,
to create a second background grid that places corners in
thin features.
The second step uses a primal method, similar to marching cubes,
over the second background grid to triangulate the isosurface.
Youngwook Kwon.
Scott Schaefer and Joe Warren,
Dual Marching Cubes: Primal Contouring of Dual Grids,
Computer Graphics Forum 24(2):195–201, 2005.
PDF (1,037k).
A clever isosurface extraction method that can often extract
thin features without using a fine grid.
It works in two steps.
The first step uses a dual octree method, similar to dual contouring,
to create a second background grid that places corners in
thin features.
The second step uses a primal method, similar to marching cubes,
over the second background grid to triangulate the isosurface.
Youngwook Kwon.
 Brian Curless and Marc Levoy,
A Volumetric Method for Building Complex Models from Range Images,
Computer Graphics (SIGGRAPH '96 Proceedings), pages 303–312, 1996.
Gnuzipped PostScript (766k) or
PDF (270k).
Slides from their talk are also available in
Gnuzipped PostScript (4,024k) or
PDF (581k).
One of the earliest and best-known papers on
building surfaces to fit point data.
Takes advantage of the properties of laser range finders,
such as your knowledge of the direction from which each point was scanned.
It has no guaranteed bounds,
but it's extremely fast and works well in practice.
Ricardo Garcia.
Brian Curless and Marc Levoy,
A Volumetric Method for Building Complex Models from Range Images,
Computer Graphics (SIGGRAPH '96 Proceedings), pages 303–312, 1996.
Gnuzipped PostScript (766k) or
PDF (270k).
Slides from their talk are also available in
Gnuzipped PostScript (4,024k) or
PDF (581k).
One of the earliest and best-known papers on
building surfaces to fit point data.
Takes advantage of the properties of laser range finders,
such as your knowledge of the direction from which each point was scanned.
It has no guaranteed bounds,
but it's extremely fast and works well in practice.
Ricardo Garcia.
 Christian Früh, Siddharth Jain, and Avideh Zakhor,
Data Processing Algorithms for Generating Textured 3D Building Facade
Meshes from Laser Scans and Camera Images,
International Journal of Computer Vision 61(2):159–184,
February 2005.
PDF (5,778k).
These folks drove a truck around Berkeley with a couple of lasers and a camera
attached, then created a real-time walk-through of the storefronts!
And you thought Britney Spears defined cool.
Peter Cottle.
Christian Früh, Siddharth Jain, and Avideh Zakhor,
Data Processing Algorithms for Generating Textured 3D Building Facade
Meshes from Laser Scans and Camera Images,
International Journal of Computer Vision 61(2):159–184,
February 2005.
PDF (5,778k).
These folks drove a truck around Berkeley with a couple of lasers and a camera
attached, then created a real-time walk-through of the storefronts!
And you thought Britney Spears defined cool.
Peter Cottle.
 Yutaka Ohtake, Alexander Belyaev, Marc Alexa, Greg Turk, and Hans-Peter Seidel,
Multi-Level Partition of Unity Implicits,
ACM Transactions on Graphics 22(3):463–470, July 2003.
Special issue on Proceedings of SIGGRAPH 2003.
The input is a cloud of points where each point has a normal vector attached,
understood to be normal to the true surface.
The output is an isosurface that approximates the original surface from which
the points were sampled.
A triangulated surface can then be extracted from the isosurface by methods
like marching cubes or dual contouring—or the isosurface can be
rendered directly.
The idea is elegant, but I suspect this method does not deal with noisy data
as well as the other papers here.
Yutaka Ohtake, Alexander Belyaev, Marc Alexa, Greg Turk, and Hans-Peter Seidel,
Multi-Level Partition of Unity Implicits,
ACM Transactions on Graphics 22(3):463–470, July 2003.
Special issue on Proceedings of SIGGRAPH 2003.
The input is a cloud of points where each point has a normal vector attached,
understood to be normal to the true surface.
The output is an isosurface that approximates the original surface from which
the points were sampled.
A triangulated surface can then be extracted from the isosurface by methods
like marching cubes or dual contouring—or the isosurface can be
rendered directly.
The idea is elegant, but I suspect this method does not deal with noisy data
as well as the other papers here.
 Michael M. Kazhdan, Matthew Bolitho, and Hugues Hoppe,
Poisson Surface Reconstruction,
Symposium on Geometry Processing 2006 (Cagliari, Italy), pages 61–70,
June 2006.
PDF (12,654k).
Like the paper above, this paper presents a method for computing an isosurface
from a cloud of points with attached normals.
This method is much more resistant to noise (which laser scans usually
have lots of), but is correspondingly more complicated.
Michael M. Kazhdan, Matthew Bolitho, and Hugues Hoppe,
Poisson Surface Reconstruction,
Symposium on Geometry Processing 2006 (Cagliari, Italy), pages 61–70,
June 2006.
PDF (12,654k).
Like the paper above, this paper presents a method for computing an isosurface
from a cloud of points with attached normals.
This method is much more resistant to noise (which laser scans usually
have lots of), but is correspondingly more complicated.
 Z. Kaufman, M. Engelberg, and M. Zager,
Fecal
Fistula: A Late Complication of Marlex Mesh Repair,
Diseases of the Colon & Rectum 24(7):543–544, October 1981.
A mesh repair paper that advocates
the use of extraperitoneal meshes to close burst abdominal manifolds.
Although both extraperitoneal and intraperitoneal meshes offer
guarantees of watertightness and high quality, intraperitoneal meshes may
become incorporated into the splenic flexure and cause a fistula,
a condition wherein the digestive manifold has a genus one greater than
it should have. The authors depict an example in which this caused the
“discharge of fecal content from the left subcostal region.”
Z. Kaufman, M. Engelberg, and M. Zager,
Fecal
Fistula: A Late Complication of Marlex Mesh Repair,
Diseases of the Colon & Rectum 24(7):543–544, October 1981.
A mesh repair paper that advocates
the use of extraperitoneal meshes to close burst abdominal manifolds.
Although both extraperitoneal and intraperitoneal meshes offer
guarantees of watertightness and high quality, intraperitoneal meshes may
become incorporated into the splenic flexure and cause a fistula,
a condition wherein the digestive manifold has a genus one greater than
it should have. The authors depict an example in which this caused the
“discharge of fecal content from the left subcostal region.”
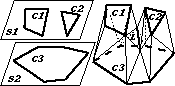 Chandrajit L. Bajaj, Edward J. Coyle, and Kwun-Nan Lin,
Surface and 3D Triangular Meshes from Planar Cross Sections,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 169–178, October 1996.
Gnuzipped PostScript (123k) or
PDF (223k).
How to reconstruct the surface or volume of a solid, given only
planar cross sections of it.
Chandrajit L. Bajaj, Edward J. Coyle, and Kwun-Nan Lin,
Surface and 3D Triangular Meshes from Planar Cross Sections,
Fifth International Meshing Roundtable (Pittsburgh, Pennsylvania),
pages 169–178, October 1996.
Gnuzipped PostScript (123k) or
PDF (223k).
How to reconstruct the surface or volume of a solid, given only
planar cross sections of it.
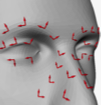 Mark Meyer, Mathieu Desbrun, Peter Schröder, and Alan H. Barr,
Discrete Differential-Geometry Operators for Triangulated 2-Manifolds,
pages 35–58 of Visualization and Mathematics III,
Hans-Christian Hege and Konrad Polthier (editors),
Springer-Verlag, Berlin, 2003.
PDF (5,660k).
A central theme of the CalTech graphics group is the development and use
of discrete versions of the ideas that form differential geometry.
This survey describes how continuous ideas like normal vectors, curvature,
and differential operators can be discretized for use with
surface triangulations.
Mark Meyer, Mathieu Desbrun, Peter Schröder, and Alan H. Barr,
Discrete Differential-Geometry Operators for Triangulated 2-Manifolds,
pages 35–58 of Visualization and Mathematics III,
Hans-Christian Hege and Konrad Polthier (editors),
Springer-Verlag, Berlin, 2003.
PDF (5,660k).
A central theme of the CalTech graphics group is the development and use
of discrete versions of the ideas that form differential geometry.
This survey describes how continuous ideas like normal vectors, curvature,
and differential operators can be discretized for use with
surface triangulations.
 Timothy D. Gatzke and Cindy M. Grimm,
Estimating Curvature on Triangular Meshes,
International Journal of Shape Modeling 12(1):1–29, June 2006.
PDF (400k).
A survey and empirical comparison of discrete curvature operators and
the circumstances under which they fail.
Pardeep Kumar.
Timothy D. Gatzke and Cindy M. Grimm,
Estimating Curvature on Triangular Meshes,
International Journal of Shape Modeling 12(1):1–29, June 2006.
PDF (400k).
A survey and empirical comparison of discrete curvature operators and
the circumstances under which they fail.
Pardeep Kumar.
 Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes, Computer Graphics
(SIGGRAPH '97 Proceedings), pages 189–198, August 1997.
Gnuzipped PostScript (3,891k) or
PDF (601k).
Slides from Hugues'
talk (PDF, 5,051k) are also available.
Hoppe's paper Progressive Meshes is the second-most cited SIGGRAPH
paper ever (after the marching cubes paper).
Whereas the first paper focused on sending geometry over slow transmission
lines, this follow-up paper applies the idea for fast rendering.
Progressively simplified triangular surfaces can be rendered at
different levels of detail, trading off resolution for rendering speed.
For example, faraway objects can be rendered with fewer triangles.
Moreover, the resolution can vary within a single mesh—for example,
finer triangles can be used at the silhouettes.
Hugues Hoppe,
View-Dependent Refinement of Progressive Meshes, Computer Graphics
(SIGGRAPH '97 Proceedings), pages 189–198, August 1997.
Gnuzipped PostScript (3,891k) or
PDF (601k).
Slides from Hugues'
talk (PDF, 5,051k) are also available.
Hoppe's paper Progressive Meshes is the second-most cited SIGGRAPH
paper ever (after the marching cubes paper).
Whereas the first paper focused on sending geometry over slow transmission
lines, this follow-up paper applies the idea for fast rendering.
Progressively simplified triangular surfaces can be rendered at
different levels of detail, trading off resolution for rendering speed.
For example, faraway objects can be rendered with fewer triangles.
Moreover, the resolution can vary within a single mesh—for example,
finer triangles can be used at the silhouettes.
 Michael Garland and Paul Heckbert,
Fast Triangular Approximation of Terrains and Height Fields,
manuscript, May 1997.
Gnuzipped PostScript (1,818k) or
PDF (690k).
For applications in Geographical Information Systems and terrain databases,
it is useful to be able to simplify triangulated terrains
for fast rendering.
The most efficient triangulation is not necessarily Delaunay, but rather has
“data-dependent” triangles chosen to best represent the terrain.
Michael Garland and Paul Heckbert,
Fast Triangular Approximation of Terrains and Height Fields,
manuscript, May 1997.
Gnuzipped PostScript (1,818k) or
PDF (690k).
For applications in Geographical Information Systems and terrain databases,
it is useful to be able to simplify triangulated terrains
for fast rendering.
The most efficient triangulation is not necessarily Delaunay, but rather has
“data-dependent” triangles chosen to best represent the terrain.
 Olga Sorkine, Daniel Cohen-Or, Rony Goldenthal, and Dani Lischinski,
Bounded-Distortion Piecewise Mesh Parameterization,
Proceedings of the Conference on Visualization '02 (Boston, Massachusetts),
pages 355–362, 2002.
PDF (3,522k).
An algorithm for mesh parametrization (see above)
that simultaneously cuts the surface mesh and computes how it is distorted.
The authors can guarantee bounds on the distortion, because in any circumstance
where it is not feasible to keep the distortion small, they cut more edges.
Olga Sorkine, Daniel Cohen-Or, Rony Goldenthal, and Dani Lischinski,
Bounded-Distortion Piecewise Mesh Parameterization,
Proceedings of the Conference on Visualization '02 (Boston, Massachusetts),
pages 355–362, 2002.
PDF (3,522k).
An algorithm for mesh parametrization (see above)
that simultaneously cuts the surface mesh and computes how it is distorted.
The authors can guarantee bounds on the distortion, because in any circumstance
where it is not feasible to keep the distortion small, they cut more edges.
 Pierre Alliez, Giuliana Ucelli, Craig Gotsman, and Marco Attene,
Recent Advances in Remeshing of Surfaces,
Chapter 2 of Shape Analysis and Structuring,
Leila de Floriani and Michela Spagnuolo (editors),
Springer, Berlin, November 2007.
PDF (14,644k).
A survey of methods to remesh a surface to improve the spacing of its vertices
and the quality of its triangles for applications like rendering,
texture mapping, editing, and creating control meshes for subdivision surfaces.
Pierre Alliez, Giuliana Ucelli, Craig Gotsman, and Marco Attene,
Recent Advances in Remeshing of Surfaces,
Chapter 2 of Shape Analysis and Structuring,
Leila de Floriani and Michela Spagnuolo (editors),
Springer, Berlin, November 2007.
PDF (14,644k).
A survey of methods to remesh a surface to improve the spacing of its vertices
and the quality of its triangles for applications like rendering,
texture mapping, editing, and creating control meshes for subdivision surfaces.
 Fakir S. Nooruddin and Greg Turk,
Simplification and Repair of Polygonal Meshes Using Volumetric
Techniques,
IEEE Transactions on Visualization and Computer Graphics
9(2):191–205, April–June 2003.
PDF (14,745k).
The geometric models produced for computer graphics are usually
“polygon soup”—full of holes and cracks and
self-intersecting polygons.
This paper describes a way of repairing these messes and producing
clean, watertight manifolds.
Fakir S. Nooruddin and Greg Turk,
Simplification and Repair of Polygonal Meshes Using Volumetric
Techniques,
IEEE Transactions on Visualization and Computer Graphics
9(2):191–205, April–June 2003.
PDF (14,745k).
The geometric models produced for computer graphics are usually
“polygon soup”—full of holes and cracks and
self-intersecting polygons.
This paper describes a way of repairing these messes and producing
clean, watertight manifolds.
 Aaron W. F. Lee, David Dobkin, Wim Sweldens, and Peter Schröder,
Multiresolution Mesh Morphing,
Computer Graphics (SIGGRAPH '99 Proceedings), (Los Angeles, California),
pages 343–350, August 1999.
PDF (42,270k).
How to morph one triangular surface mesh into another.
Aaron W. F. Lee, David Dobkin, Wim Sweldens, and Peter Schröder,
Multiresolution Mesh Morphing,
Computer Graphics (SIGGRAPH '99 Proceedings), (Los Angeles, California),
pages 343–350, August 1999.
PDF (42,270k).
How to morph one triangular surface mesh into another.
 Mathieu Desbrun, Mark Meyer, Peter Schröder, and Alan H. Barr,
Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow,
Computer Graphics (SIGGRAPH '99 Proceedings) (Los Angeles, California),
pages 317–324, August 1999.
PDF (1,735k).
When you generalize the idea of mesh smoothing to a surface triangulation,
things can go wrong—for instance, the surface could shrink inward.
Here's a sophisticated method for smoothing noisy surfaces well.
Mathieu Desbrun, Mark Meyer, Peter Schröder, and Alan H. Barr,
Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow,
Computer Graphics (SIGGRAPH '99 Proceedings) (Los Angeles, California),
pages 317–324, August 1999.
PDF (1,735k).
When you generalize the idea of mesh smoothing to a surface triangulation,
things can go wrong—for instance, the surface could shrink inward.
Here's a sophisticated method for smoothing noisy surfaces well.
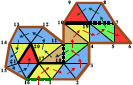 Jarek Rossignac,
Edgebreaker: Connectivity Compression for Triangle Meshes,
Technical Report GIT-GVU-98-35, GVU Center, Georgia Institute of Technology,
October 1998.
Gnuzipped PostScript (125k) or
PDF (173k).
A method for compression of triangular meshes for
rapid transmission over slow communication lines.
Jarek Rossignac,
Edgebreaker: Connectivity Compression for Triangle Meshes,
Technical Report GIT-GVU-98-35, GVU Center, Georgia Institute of Technology,
October 1998.
Gnuzipped PostScript (125k) or
PDF (173k).
A method for compression of triangular meshes for
rapid transmission over slow communication lines.
 Guy E. Blelloch, Gary L. Miller, and Dafna Talmor,
Developing a Practical Projection-Based Parallel Delaunay Algorithm,
Proceedings of the Twelfth Annual Symposium on Computation Geometry
(Philadelphia, Pennsylvania), pages 186–195, ACM, May 1996.
Gnuzipped PostScript (226k) or
PDF (518k).
Slides from Dafna's talk are also available in
Gnuzipped PostScript (303k) or
PDF (637k).
This is the only parallel Delaunay triangulation algorithm I am aware of
that is good in both theory and practice.
Guy E. Blelloch, Gary L. Miller, and Dafna Talmor,
Developing a Practical Projection-Based Parallel Delaunay Algorithm,
Proceedings of the Twelfth Annual Symposium on Computation Geometry
(Philadelphia, Pennsylvania), pages 186–195, ACM, May 1996.
Gnuzipped PostScript (226k) or
PDF (518k).
Slides from Dafna's talk are also available in
Gnuzipped PostScript (303k) or
PDF (637k).
This is the only parallel Delaunay triangulation algorithm I am aware of
that is good in both theory and practice.
 Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Streaming Computation of Delaunay Triangulations,
ACM Transactions on Graphics 25(3):1049–1056, July 2006.
Special issue on Proceedings of SIGGRAPH 2006.
PDF (9,175k).
Streaming is a method for out-of-core computation that makes it possible
to compute Delaunay triangulations of billions of points
on an ordinary laptop computer.
See also the
video
(your choice of iPod, QT/mpeg4, DivX, MW/avi, MW/mpg1, or orig mov) from
the Proceedings of the Fifteenth Video Review of Computational Geometry.
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Streaming Computation of Delaunay Triangulations,
ACM Transactions on Graphics 25(3):1049–1056, July 2006.
Special issue on Proceedings of SIGGRAPH 2006.
PDF (9,175k).
Streaming is a method for out-of-core computation that makes it possible
to compute Delaunay triangulations of billions of points
on an ordinary laptop computer.
See also the
video
(your choice of iPod, QT/mpeg4, DivX, MW/avi, MW/mpg1, or orig mov) from
the Proceedings of the Fifteenth Video Review of Computational Geometry.
 Peter Su and Robert L. Scot Drysdale,
A Comparison of Sequential Delaunay Triangulation Algorithms,
Proceedings of the Eleventh Annual Symposium on Computational Geometry
(Vancouver, British Columbia, Canada), pages 61–70, ACM, June 1995.
Gnuzipped PostScript (93k) or
PDF (229k).
A comparison of the speed of
two-dimensional Delaunay triangulation algorithms.
Unfortunately, they don't have an implementation of the divide-and-conquer
algorithm, which is probably the fastest algorithm in practice.
You might also want to look at Chapter 2 of Peter Su's dissertation
for additional figures and algorithmic details.
Gnuzipped PostScript (383k) or
PDF (892k).
Peter Su and Robert L. Scot Drysdale,
A Comparison of Sequential Delaunay Triangulation Algorithms,
Proceedings of the Eleventh Annual Symposium on Computational Geometry
(Vancouver, British Columbia, Canada), pages 61–70, ACM, June 1995.
Gnuzipped PostScript (93k) or
PDF (229k).
A comparison of the speed of
two-dimensional Delaunay triangulation algorithms.
Unfortunately, they don't have an implementation of the divide-and-conquer
algorithm, which is probably the fastest algorithm in practice.
You might also want to look at Chapter 2 of Peter Su's dissertation
for additional figures and algorithmic details.
Gnuzipped PostScript (383k) or
PDF (892k).
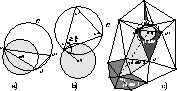 Olivier Devillers,
Improved Incremental Randomized Delaunay Triangulation,
Proceedings of the Fourteenth Annual Symposium on Computation Geometry
(Minneapolis, Minnesota), pages 106–115, ACM, June 1998.
Gnuzipped PostScript (113k) or
PDF (195k).
Also check out the technical report by the same name
which has bigger figures (better for presenting)
and perhaps more useful information.
Gnuzipped PostScript (218k) or
PDF (346k).
This paper describes an interesting randomized dynamic point location method
for incremental Delaunay triangulation.
It works with vertex deletions, as well as insertions.
Good in both theory and practice.
I find the analysis of the running time for point location to be
beautifully elegant.
Olivier Devillers,
Improved Incremental Randomized Delaunay Triangulation,
Proceedings of the Fourteenth Annual Symposium on Computation Geometry
(Minneapolis, Minnesota), pages 106–115, ACM, June 1998.
Gnuzipped PostScript (113k) or
PDF (195k).
Also check out the technical report by the same name
which has bigger figures (better for presenting)
and perhaps more useful information.
Gnuzipped PostScript (218k) or
PDF (346k).
This paper describes an interesting randomized dynamic point location method
for incremental Delaunay triangulation.
It works with vertex deletions, as well as insertions.
Good in both theory and practice.
I find the analysis of the running time for point location to be
beautifully elegant.
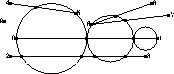 Herbert Edelsbrunner and Tiow Seng Tan,
An Upper Bound for Conforming Delaunay Triangulations,
Discrete & Computational Geometry 10(2):197–213, August 1993.
Gnuzipped PostScript (67k) or
PDF (248k).
The algorithm that achieves the best known bound for the number of
Steiner points needed to create a Delaunay triangulation
that conforms to a specified PSLG.
For a brief description of this result,
see Bern and Eppstein, pages 37–38.
Herbert Edelsbrunner and Tiow Seng Tan,
An Upper Bound for Conforming Delaunay Triangulations,
Discrete & Computational Geometry 10(2):197–213, August 1993.
Gnuzipped PostScript (67k) or
PDF (248k).
The algorithm that achieves the best known bound for the number of
Steiner points needed to create a Delaunay triangulation
that conforms to a specified PSLG.
For a brief description of this result,
see Bern and Eppstein, pages 37–38.