TILT: Transform Invariant Low-rank Textures
One of the fundamental problems in computer vision is to identify feature points or salient regions in images. Since these distinctive points or regions are normally used to establish correspondence or measure similarity across different images, they are desired to have properties that are somewhat stable or invariant under transformations incurred by changes in viewpoint or illumination. Thus, the problem is to extract regions in a 2D image that correspond to a very rich class of regular patterns on a planar surface in 3D.
The basic idea of our approach is to view each image as a matrix and seek a transformation that gives rise to a low-rank matrix subject to sparse errors. We consider a m x n image I0 of a texture to be of low-rank if the rank of the matrix I0 is much smaller than both m and n. Suppose we are given an image I of an object with a window containing a low-rank texture. The scene could be warped and corrupted by errors or occlusions, and therefore, I does not have low rank. We model the warping by a global domain transformation belonging to a finite-dimensional group. Thus, we have a transformation τ such that the transformed image I ο τ has low rank, subject to a sparse error term E that compensates for large, gross errors such as partial occlusions. We can formulate this problem in Lagrangian form as follows:
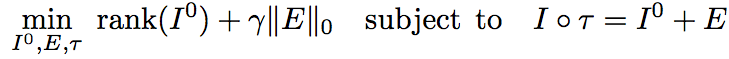
where ||E||0 represents the number of non-zero entries in the matrix E, and γ is an appropriately chosen positive constant. Although the above problem follows naturally from our problem formulation, the cost function is highly non-convex and discontinuous, and the equality constraint is highly non-linear. Thus, it is intractable, and of little practical use.
Recent work in compressed sensing and matrix completion suggests that the above problem can be efficiently solved, under quite general conditions, by replacing the cost function with its convex surrogate, as shown below:
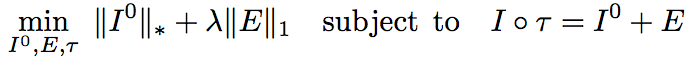
where || ||* represents the matrix nuclear norm (the sum of singular values), || ||1 represents the matrix 1-norm (the sum of absolute values of the entries), and λ is a positive weighting factor. Although the cost function is convex and continuous, the constraint is non-linear. Therefore, we solve the optimization problem by iterative linearization of the constraint. We also add a couple of extra constraints to avoid converging to a local minima. For more details on the algorithm and implementation, please refer to our paper.
The videos below demonstrate the working of the TILT algorithm. The input image is that of a building whose facade is not parallel to the image plane. In the video, each frame corresponds to one iteration of the TILT algorithm. In the input video (left), the input window is shown as a red box, and the output of each iteration is shown by a green box. The transformation is applied to the entire image in the output video (right). The final frame shows the low-rank representation returned by the TILT algorithm. The TILT algorithm computes the correct transformation despite the presence of occlusions such as tree branches in the image.
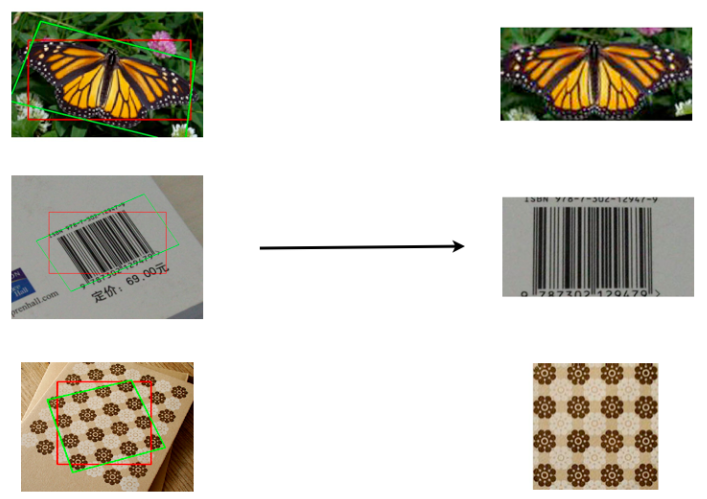
TILT: Transform Invariant Low-rank Textures,| Input images of various objects chosen from the internet. The red box encloses the initial region of interest. The green box represents the recovered transformation that aligns the object to a canonical form exploiting the inherent symmetry in it. | Low-rank representation of the object when considered as a matrix. The low rank is due to the fact that the the object exhibits some form of reflectional symmetry. | |
One of the fundamental problems in computer vision is to identify feature points or salient regions in images. Since these distinctive points or regions are normally used to establish correspondence or measure similarity across different images, they are desired to have properties that are somewhat stable or invariant under transformations incurred by changes in viewpoint or illumination. Thus, the problem is to extract regions in a 2D image that correspond to a very rich class of regular patterns on a planar surface in 3D.
The basic idea of our approach is to view each image as a matrix and seek a transformation that gives rise to a low-rank matrix subject to sparse errors. We consider a m x n image I0 of a texture to be of low-rank if the rank of the matrix I0 is much smaller than both m and n. Suppose we are given an image I of an object with a window containing a low-rank texture. The scene could be warped and corrupted by errors or occlusions, and therefore, I does not have low rank. We model the warping by a global domain transformation belonging to a finite-dimensional group. Thus, we have a transformation τ such that the transformed image I ο τ has low rank, subject to a sparse error term E that compensates for large, gross errors such as partial occlusions. We can formulate this problem in Lagrangian form as follows:
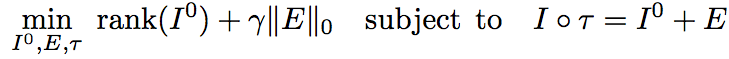
Recent work in compressed sensing and matrix completion suggests that the above problem can be efficiently solved, under quite general conditions, by replacing the cost function with its convex surrogate, as shown below:
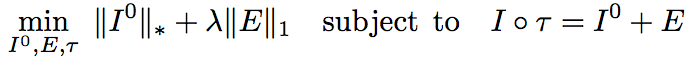
The videos below demonstrate the working of the TILT algorithm. The input image is that of a building whose facade is not parallel to the image plane. In the video, each frame corresponds to one iteration of the TILT algorithm. In the input video (left), the input window is shown as a red box, and the output of each iteration is shown by a green box. The transformation is applied to the entire image in the output video (right). The final frame shows the low-rank representation returned by the TILT algorithm. The TILT algorithm computes the correct transformation despite the presence of occlusions such as tree branches in the image.
Sample Code and Data
A MATLAB implementation of our algorithm, along with some sample data, can be downloaded at the following link:
Transform Invariant Low-rank Textures (last updated on April 21, 2012 )
We have provided a few examples in the package. For more sample images of building facades obtained from the internet, please click here.
If you use the above code or data, please cite our paper.
Transform Invariant Low-rank Textures (last updated on April 21, 2012 )
We have provided a few examples in the package. For more sample images of building facades obtained from the internet, please click here.
If you use the above code or data, please cite our paper.
Publications
Zhengdong Zhang, Arvind Ganesh, Xiao Liang, and Yi Ma. Submitted to International Journal of Computer Vision (IJCV), December 2010.
[Conference version presented at ACCV 2010] [arXiv version]
Please contact the webmaster Arvind Ganesh if you have any questions or comments regarding this work.