Robust Photometric Stereo via Low-Rank Matrix Completion and Recovery
Photometric stereo is a well-studied problem in computer vision. The basic problem is to estimate the normal map of a scene given multiple 2D images taken under the same viewpoint but different lighting conditions. The problem can be further subdivided into calibrated and uncalibrated stereo. In the former, the lighting directions are known while in the latter they are not.
The typical assumption in photometric stereo is that the object of interest obeys a Lambertian reflectance model. This is a simple model that relates the surface normal n, lighting direction l, and pixel intensity I through the following equation:
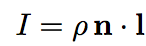
where ρ denotes the diffuse albedo, and the multiplication is a vector inner product. Suppose D denotes the image matrix each of whose columns represents an image (each image is stacked as a vector). Then, using the ideal Lambertian model, it can be shown that the matrix D has rank atmost 3, irrespective of the size of each image and the total number of input images. However, this low rank structure is seldom observed in practice since the images are often corrupted by shadows (both attached and cast), and by specularities. These errors are concentrated on a small number of pixels in each image and can have very large magnitude. Our goal is to recover the low rank structure from the input matrix, despite the presence of large, sparse errors.
Using recent ideas from the theory of sparse and low-rank matrix decomposition, we propose recovering the ideal low rank structure using the following convex optimization problem:
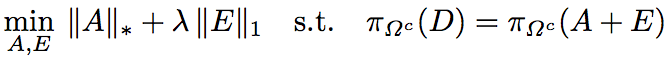
where ||E||1 represents the matrix 1-norm (sum of absolute values of the entries of E), ||A||* represents the matrix nuclear norm (sum of singular values of A), Ω denotes the set of pixels that are occluded by shadows (detected by simple pixel thresholding), π represents the orthogonal projection operator onto a subspace, and λ is a weighting parameter. We solve this optimization problem efficiently using the method of Augmented Lagrange Multipliers. Once the low-rank matrix is recovered, the normal map can be easily computed. For more details on the algorithm and implementation, please refer to our paper.
Convex Optimization Based Low-Rank Matrix Completion and Recovery for Photometric Stereo and Factor Classification, |
| Input images of an object taken under different lighting conditions (top). The images are corrupted by shadows and specularities that violate the Lambertian assumption. The low-rank structure inherent in the geometry of the problem enables us to recover the normal map (bottom) accurately and efficiently. |
Photometric stereo is a well-studied problem in computer vision. The basic problem is to estimate the normal map of a scene given multiple 2D images taken under the same viewpoint but different lighting conditions. The problem can be further subdivided into calibrated and uncalibrated stereo. In the former, the lighting directions are known while in the latter they are not.
The typical assumption in photometric stereo is that the object of interest obeys a Lambertian reflectance model. This is a simple model that relates the surface normal n, lighting direction l, and pixel intensity I through the following equation:
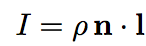
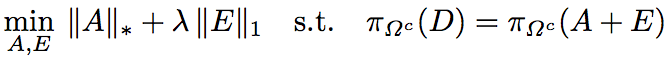
Publications
Lun Wu, Arvind Ganesh, Boxin Shi, Yasuyuki Matsushita, Yongtian Wang, and Yi Ma. Submitted to IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), August 2011.
Robust Photometric Stereo via Low-Rank Matrix Completion and Recovery,
Lun Wu, Arvind Ganesh, Boxin Shi, Yasuyuki Matsushita, Yongtian Wang, and Yi Ma. In Proceedings of Asian Conference on Computer Vision, November 2010.
Please contact the webmaster Arvind Ganesh if you have any questions or comments regarding this work.