INTRODUCTION
Suppose that we have a rank-r matrix A of size m x n, where r << min(m,n). In many engineering problems, the entries of the matrix are often corrupted by errors or noise, some of the entries could even be missing, or only a set of measurements of the matrix is accessible rather than its entries directly. In general, we model the observed matrix D to be a set of linear measurements on the matrix A, subject to noise and gross corruptions i.e., D = L(A) + η, where L is a linear operator, and η represents the matrix of corruptions. We seek to recover the true matrix A from D.
Suppose that L is the identity operator and the entries of η are independent and identically distributed according to a isotropic Gaussian distribution, then classical PCA provides the optimal estimate to A. The solution involves computing the Singular Value Decomposition (SVD) of D, and projecting each column of D onto the linear subspace spanned by the r principal singular vectors of D to get the estimate A.
The possibility of efficient computation along with optimality properties in the presence of Gaussian noise has propelled PCA into becoming one of the most popular algorithms in use in data analysis and compression. However, real-world data is often corrupted by large errors, or can even be incomplete. Therefore, the classical PCA estimate can be far from the underlying true distribution of the data owing to its high sensitivity to large errors, and there is no theoretical framework to deal with incomplete or missing data. Moreover, the rank r of the matrix A needs to be known apriori, which is seldom the case in real problems.
We consider the special scenario where η is zero and L is the matrix subsampling operator i.e., L(A) is a subset of all entries of A. Thus, the problem is to use information from some entries of A to infer its missing entries. A natural approach to solving this problem is to formulate it as a rank-minimization problem:
We now consider the case where L is the identity operator and η is a sparse matrix (i.e., most of its entries are zero) but whose non-zero entries can be practically unbounded. Since the rank r of A is unknown, the problem is to find the matrix of lowest rank that could have generated D when added to an unknown sparse matrix η. Mathematically, for an appropriate choice of parameter γ > 0, we have the following combinatorial optimization problem to solve:
| Problem Description | Classical PCA | Matrix Completion | Robust PCA |
Problem
Description
Suppose that we have a rank-r matrix A of size m x n, where r << min(m,n). In many engineering problems, the entries of the matrix are often corrupted by errors or noise, some of the entries could even be missing, or only a set of measurements of the matrix is accessible rather than its entries directly. In general, we model the observed matrix D to be a set of linear measurements on the matrix A, subject to noise and gross corruptions i.e., D = L(A) + η, where L is a linear operator, and η represents the matrix of corruptions. We seek to recover the true matrix A from D.
Classical
Principal Component Analysis (PCA)
Suppose that L is the identity operator and the entries of η are independent and identically distributed according to a isotropic Gaussian distribution, then classical PCA provides the optimal estimate to A. The solution involves computing the Singular Value Decomposition (SVD) of D, and projecting each column of D onto the linear subspace spanned by the r principal singular vectors of D to get the estimate A.
The possibility of efficient computation along with optimality properties in the presence of Gaussian noise has propelled PCA into becoming one of the most popular algorithms in use in data analysis and compression. However, real-world data is often corrupted by large errors, or can even be incomplete. Therefore, the classical PCA estimate can be far from the underlying true distribution of the data owing to its high sensitivity to large errors, and there is no theoretical framework to deal with incomplete or missing data. Moreover, the rank r of the matrix A needs to be known apriori, which is seldom the case in real problems.
 |
 |
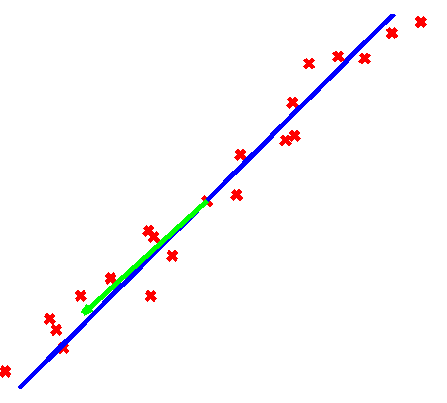
| Samples (red) from a one-dimensional subspace (blue) corrupted by small Gaussian noise. The output of classical PCA (green) is very close to the true subspace despite all samples being noisy. | Samples (red) from a one-dimensional subspace (blue) corrupted by sparse, large errors. The principal component (green) is quite far from the true subspace even when over three-fourths of the samples are uncorrupted. |
Matrix
Completion
We consider the special scenario where η is zero and L is the matrix subsampling operator i.e., L(A) is a subset of all entries of A. Thus, the problem is to use information from some entries of A to infer its missing entries. A natural approach to solving this problem is to formulate it as a rank-minimization problem:
minX
rank(X)
subject to L(X) = D.
However, this
optimization problem is intractable and hence, of little practical use.
Since the matrix nuclear norm (i.e., the sum of its singular values),
represented as ||.||*,
is the best convex approximation to the rank function, we instead solve
minX
||X||*
subject to L(X) = D.It has been shown
that this convex relaxation can exactly recover the true low-rank
matrix A under quite general conditions [Candès
and Recht, 2008]. Furthermore, it has been shown that the
recovery is stable to small, bounded noise [Candès
and Plan, 2009], i.e., when the entries of η are
non-zero and bounded.
Robust
Principal Component Analysis (RPCA)
We now consider the case where L is the identity operator and η is a sparse matrix (i.e., most of its entries are zero) but whose non-zero entries can be practically unbounded. Since the rank r of A is unknown, the problem is to find the matrix of lowest rank that could have generated D when added to an unknown sparse matrix η. Mathematically, for an appropriate choice of parameter γ > 0, we have the following combinatorial optimization problem to solve:
minX,E
rank(X)
+ γ ||E||0
subject to D = X + E,
where ||.||0
is the counting norm (i.e., the number of non-zero entries in the
matrix).
Since this problem
cannot be efficiently solved, we consider its convex relaxation instead:
minX,E
||X||*
+ λ ||E||1
subject to
D = X + E,
where ||.||1
represents the matrix 1-norm (i.e.,
the sum of absolute values of all entries of the matrix), and
λ
is a positive constant that scales
as m-½.We
call the above convex program the Robust
Principal Component Analysis (RPCA). This formulation
performs well in practice, recovering the true low-rank solution even
when upto a third of the observations are grossly corrupted. It also
comes with excellent theoretical guarantees. For example, for generic
matrices A,
it can be shown to successfully correct a constant fraction of errors,
even when the rank of A
is nearly proportional to the ambient dimension: rank(A) = C m / log(m). Please refer to
[Candès et al, 2009] for more details.
The RPCA algorithm is straightforward in that it is essentially a convex optimization problem or more specifically, it can be recast as a semidefinite program (SDP). It is well-known that SDPs are tractable and interior point methods are a popular class of algorithms to solve them. However, while interior point methods offer superior accuracy and convergence rates, they do not scale very well with the size of the matrix - computing the Newton step every iteration has a complexity of O(m6). As a result, off-the-shelf packages to solve SDPs can often handle matrices of sizes only upto about 70 x 70.
We approach the RPCA optimization problem in two different ways. In the first approach, we use a first-order method to solve the primal problem directly. Our algorithm is a special case of a more general class of algorithms called proximal gradient algorithms, and is a direct application of the more general FISTA algorithm. The algorithm has a theoretical iteration complexity of O(k-2), however in practice, we observe a faster convergence rate. The computational bottleneck of each iteration is a Singular Value Decomposition (SVD) computation, while the other steps involve simple matrix operations and are natually amenable to parallelized operations.
The second approach to solving the RPCA optimization problem is to formulate and solve the dual problem, and retrieve the primal solution from the dual optimal solution. The dual problem to the RPCA can be written as
The RPCA algorithm is straightforward in that it is essentially a convex optimization problem or more specifically, it can be recast as a semidefinite program (SDP). It is well-known that SDPs are tractable and interior point methods are a popular class of algorithms to solve them. However, while interior point methods offer superior accuracy and convergence rates, they do not scale very well with the size of the matrix - computing the Newton step every iteration has a complexity of O(m6). As a result, off-the-shelf packages to solve SDPs can often handle matrices of sizes only upto about 70 x 70.
We approach the RPCA optimization problem in two different ways. In the first approach, we use a first-order method to solve the primal problem directly. Our algorithm is a special case of a more general class of algorithms called proximal gradient algorithms, and is a direct application of the more general FISTA algorithm. The algorithm has a theoretical iteration complexity of O(k-2), however in practice, we observe a faster convergence rate. The computational bottleneck of each iteration is a Singular Value Decomposition (SVD) computation, while the other steps involve simple matrix operations and are natually amenable to parallelized operations.
The second approach to solving the RPCA optimization problem is to formulate and solve the dual problem, and retrieve the primal solution from the dual optimal solution. The dual problem to the RPCA can be written as
maxY ⟨D,Y⟩
subject to J(Y) ≤ 1,
where ⟨A,B⟩ = trace(ATB), J(Y) =
max( ||Y||2 , λ-1|Y|∞ ), ||.||2
represents the matrix spectral norm, and |.|∞ represents the matrix
infinite norm (i.e.,
the maximum absolute value of the matrix entries).
The above dual
problem can be
solved by constrained steepest ascent.
The highlight of this method is that it does not require a full SVD computation every iteration. Please refer to our paper for more details on
fast algorithms to solve the RPCA problem.