A Brief Introduction
Our approach to clustering and classification is based on the principle of Lossy Minimum Description Length. We measure the number of bits needed to code the data
 upto distortion
upto distortion 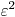 using the following formula (see our PAMI '07 paper for details):
using the following formula (see our PAMI '07 paper for details):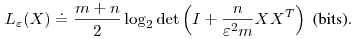
Clustering
Suppose the data are partitioned into disjoint subsets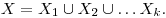 If we encode each subset separately, the total number of bits required is
If we encode each subset separately, the total number of bits required is

The second term in this equation counts then number of bits needed to represent the membership of the m samples in the k subsets (i.e., by Huffman coding).
Globally minimizing is a combinatorial problem. Nevertheless, the following
agglomerative algorithm is quite effective for segmenting data lying on
subspaces of varying dimension. It initially treats each subject as its
own group, iteratively merging pairs of groups so that the resulting
coding length is minimal. The algorithm terminates when it can no
longer reduce the coding length.
is a combinatorial problem. Nevertheless, the following
agglomerative algorithm is quite effective for segmenting data lying on
subspaces of varying dimension. It initially treats each subject as its
own group, iteratively merging pairs of groups so that the resulting
coding length is minimal. The algorithm terminates when it can no
longer reduce the coding length.

Classification
In this setting we are given training data from k classes, and a test sample x. The number of additional bits needed to code x together with the i-th class is
from k classes, and a test sample x. The number of additional bits needed to code x together with the i-th class is
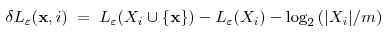
Here, the third term counts the number of bits needed to encode the assignment of x to the i-th class.

The optimal segmentation minimizes number of bits needed to encode the segmented data upto distortion 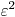 . . |
Suppose the data are partitioned into disjoint subsets
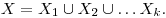 If we encode each subset separately, the total number of bits required is
If we encode each subset separately, the total number of bits required is 
Globally minimizing
 is a combinatorial problem. Nevertheless, the following
agglomerative algorithm is quite effective for segmenting data lying on
subspaces of varying dimension. It initially treats each subject as its
own group, iteratively merging pairs of groups so that the resulting
coding length is minimal. The algorithm terminates when it can no
longer reduce the coding length.
is a combinatorial problem. Nevertheless, the following
agglomerative algorithm is quite effective for segmenting data lying on
subspaces of varying dimension. It initially treats each subject as its
own group, iteratively merging pairs of groups so that the resulting
coding length is minimal. The algorithm terminates when it can no
longer reduce the coding length. 
The algorithm automatically selects the number of groups, and is robust to noise and outliers. To read further, please see our PAMI '07 Paper.
Classification
| Assign the test sample to the class of training data that minimizes the number of bits needed to code it together with the training data |
In this setting we are given training data
 from k classes, and a test sample x. The number of additional bits needed to code x together with the i-th class is
from k classes, and a test sample x. The number of additional bits needed to code x together with the i-th class is 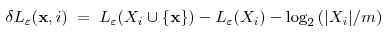

This algorithm produces a family of classifiers, indexed by distortion
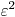 ,
which generalize the classical MAP classifier. The distortion can be
viewed as inducing a regularization effect, improving performance with
finite samples and degenerate distrubtions in high-dimensional spaces,
without sacrificing asymptotic optimality. To read more, see our preprint on MICL.
,
which generalize the classical MAP classifier. The distortion can be
viewed as inducing a regularization effect, improving performance with
finite samples and degenerate distrubtions in high-dimensional spaces,
without sacrificing asymptotic optimality. To read more, see our preprint on MICL. The use of lossy coding distinguishes both approaches from traditional
(lossless) Minimum Description Length (MDL) techniques. Lossy coding is
especially relevant when the data contain degenerate structures
such as low-dimensional subspaces or submanifolds. Classical approaches
become ill-defined in this case, but lossy coding effectively
regularizes the distribution, allowing the same algorithms to handle
both degenerate and generic data.
To read more, please visit our references page.