|
University of California EECS Dept, CS Division |
||
|
TA: Laura Downs TA: Jordan Smith |
CS184: Foundations of Computer Graphics |
Prof. Carlo H. Séquin Spring 1998 |
Scanline algorithms have a variety of applications in computer graphics and related fields. These notes contain some details and hints concerning the programming assignments relating to scan conversion of polygons, hidden feature elimination, and shaded rendering. The most important thing to keep in mind when implementing an algorithm at the pixel level is to have a clear paradigm how geometry specified in floating-point precision is mapped into integer valued pixels - and to stick to that model religiously !
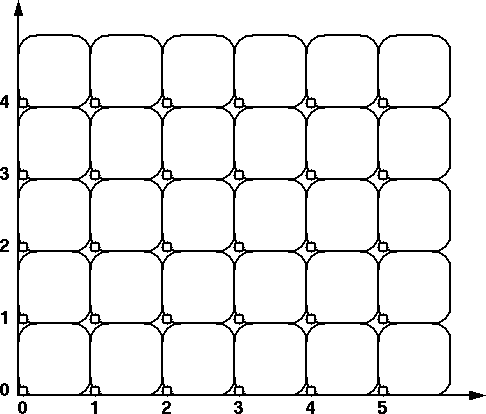
We will assume that each pixel is the square area between integer coordinates;
pixel (x, y) lies between x and x+1 and between
y and y+1.
To render a point, we turn on the pixel that gets hit by that point,
To draw a "thin" line from location (a, b) to
(c, d), we turn on every pixel that gets touched by
that line.
However, in general we will convert every task into an
area rendering task.
Thus to render a line of a particular width, we sweep a brush of the
right size and shape and define a swept area.
To render any area, we use the lower left corner of
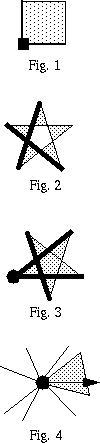
every pixel as a sampling spot (Fig.1) and turn on every
pixel whose sampling spot lies "inside" the specified area.
What is "inside" a polygon is determined by either the
"parity rule" (Fig. 2) or by the "winding number";
for this assignment we use the winding number (Fig. 3).
To make the model consistent, we have to also define that the
left-facing borders and any lower horizontal borders of an area, i.e.,
all contour segments with direction
angles >180o and <=360o, also belong to the "inside" of a polygonal area.
For complete consistency we also define that a polygon only owns those vertices for
which it covers some nonzero span immediately to the right of it (Fig.
4).
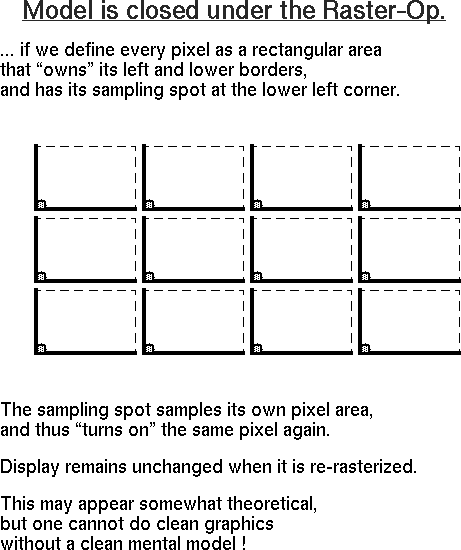
This is different from what you read in the book, but it will simplify your reasoning about what exactly to do in the scanline process. Also, we can develop the area rasterization algorithm directly, without any reference to a special line- drawing algorithm (for which we do not have time). To make the model closed under subsequent rasterization operations, a pixel "owns" its left and lower borders, as well as the lower left corner point. As a result, to render the point at integer location (x, y), we would have to turn on the square pixel (x, y) which lies above and to the right of that location, - which seems to be entirely reasonable.
The key idea is to sample the polygon at all integer y-values on a row-by-row basis, using the lower left corner of each pixel as a sampling spot to check whether the polygon is present. Then we output horizontal spans corresponding to the thus created sections through the polygon.
Transform your polygon from the canonical view half-cube to the pixel-based screen coordinates for the chosen viewport by appropriate scaling and translating in x and y; keep the z-values as they are. Homogenize your points to get their final, projected x, y, and z-values. (In order to keep full accuracy, do not convert x and y to integers.) Now create an edge table (ET) of all the edges in your clipped polygon. These edges should be bucket sorted by their minimal y-values to facilitate bottom-up scanning over all edges. Specifically, bucket i gets all edges that have a lower endpoint with i-1 < y <= i. (Bucket i should contain all edges with ceil(ymin)=i.) Overall, there will be as many y-buckets as there are pixel rows in your screen `window'. Within each bucket, sort these edges by ascending x-values of the minimum-y endpoints.
If the two endpoints of an edge lie in the same y-bucket, it does not by itself contribute to the definition of any output span, since it does not have any intersection with our sampling scan lines. Depending on your algorithm, you may still keep these horizontal edges for topological consistency. It is often desirable that for each edge you can readily find the predecessor and the successor edges in the polygon contour. If you keep horizontal edges, the vertex with the lower x-value is considered the minimal endpoint.
In addition to this static edge table, there is a dynamic active edge list (AEL) that contains all the edges that are crossing the current sampling scan-line. This data structure is updated as the scan-line steps from one y-value to the next. For efficiency, we do not determine from scratch which polygon edges intersect the current scan-line, but use an incremental method. The intersecting edges that we have to deal with are the intersecting edges from the previous scan-line, plus the new edges starting in the upward direction in the current y-bucket, minus the edges that terminate in the current y-bucket. Such updating is necessary only when the scan-line sweeps across one of the polygon vertices. Horizontal edges will be added and removed in the same step; they only help us to track the connectivity of complicated polygon contours.
After updating the AEL through the current y-bucket, we determine the x-values of all edge intersections at value y+1, sort them by their x-values, and mark them as "in" or "out" depending on whether the polygon contour crosses the scan-line in the downward or upward direction. In the direction of increasing x along the scan-line, we maintain a cumulative count of the number of in-crossings minus the number of out-crossings. As long as this number is different from zero, we output a horizontal line segment to the display. Such a contiguous sequence of pixels between two intersections is called a span.
When a vertex is processed that has one edge coming from below the current bucket and the other edge continuing upward to another bucket, the new edge can simply be inserted in place of the old edge. This does not work if the vertex has two upward going edges. In this case, the vertex coordinates themselves may be taken as the initial insert position of the new edge. A simpler, more brute force approach would simply pile up the new edges at the left end of the scan line and let them be moved into place by the bubble sort (see below).
In search of efficiency, we determine the locations of the intersection points by an incremental method. For each edge that gets added to the AEL, we determine the reciprocal slope dx/dy, and calculate the exact x-value of the first intersection with a scan-line. All the intersections with the following scan-lines can then be computed by simply adding dx to the previous x-value (dy=1).
For the more general case of polygons with intersecting edges, we need to maintain the edge intersections with the AEL in x-sorted order. Since the changes from the previous sorted state are likely to be small, this can be done effectively with a bubble sort: From left to right you check adjacent edge intersections for proper x-order. If they are out of line, you swap them. You continue to swap an edge to the left until it has reached its proper place, then you continue with the next pair of neighbors that has not yet been examined.
With all the intersection points known and sorted, we now make a
pass from left to right through the AEL and output a span of pixels
from every intersection point that marks a polygon entry (winding
number != 0) to the next intersection point representing the exit
(W.N. = 0) from the polygon.
Since pixels must have integer x-values, the real
x-values of the intersections have to be converted into integer
pixel addresses. For our choice of lower-left sampling point, the
proper conversion is via the ceiling operation.
Pixels from
ceil(xmin) to
ceil(xmax-1) are activated.
This task is very similar to the scan conversion above, except that there are now many polygons, and that the polygons may overlap or penetrate each other. We will focus here just on the enhancements to the scan-conversion algorithm that are necessary to achieve hidden feature elimination.
For this assignment we will implement a z-buffer algorithm in software. Allocate an array of width by height pixels that can each store 8-bit values for r, g, b, and z. All the polygons in the scene will be individually scan-converted into this discrete raster, but an individual pixel will only be written into this array, if its z-value is larger than the z-value already present at that pixel location. Before we begin rendering, this whole buffer is initialized to the smallest value representable in the bits dedicated to storing z-information. To make the calculation of z at each location efficient, all vertices should be transformed into 3D screen coordinates, and the plane equations for each polygon should be determined for this coordinate system, so that the depth at each pixel can also be determined incrementally.
As we scan each polygon individually, we maintain an Active Edge List (AEL) This is the continually changing dynamic data structure that represents what is happening on the current scanline. It contains an entry for every edge whose projection crosses the current scanline. These entries carry some crucial information to make the geometrical update efficient, such as:
For each polygon, we find the vertex with the minimal y-value and start our scan-conversion with the y-bucket into which this vertex falls. Stepping through all subsequent integer y-values until the active edge list becomes empty again, we do the following for each display scanline:
The determination of all the intersections between the projections of the polygon edges and the current sweep-plane position follows the approach used for scan-converting polygons. By processing all the vertices in the current y-bucket, starting edges can be added to the AEL and ending edges can be removed. After this topological update, we perform a geometrical update and calculate the current x- and z-value for all edges by adding dx/dy and dz/dy, respectively. We then re-sort the AEL by exchanging out-of-order neighbors.
With all the intersection points known and sorted, we now make a pass from left to right through the AEL. For every intersection segment, we go through a tight inner loop and compute its depth for all the integer x-positions covered by this span. We compare the computed values with the contents of the z-buffer, and if the new value is more positive, it is written into the buffer and the corresponding pixel value is set to the color of the current pixel.
If we want to produce continuously varying shading as is appropriate for a curved surface, we add some further information to the above static and dynamic data structures, and also do some additional processing when we process individual spans in the x-traversal. First we need to carry along with each vertex an illumination value that has been calculated in world coordinates where accurate information about normals and angles is still available. For each face sent to the display, we will then interpolate between the light values at the vertices; again, for efficiency's sake, this interpolation is done incrementally. With each active edge we carry the increment values dr/dy, dg/dy, and db/dy that tell by how much the intensities change from one scanline to the next; and for each segment we carry the dr/dx, dg/dx, db/dx-values that indicates how much the color changes from pixel to pixel.
![]()
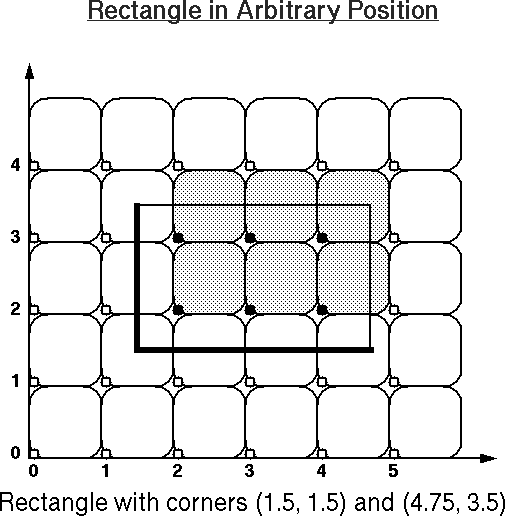
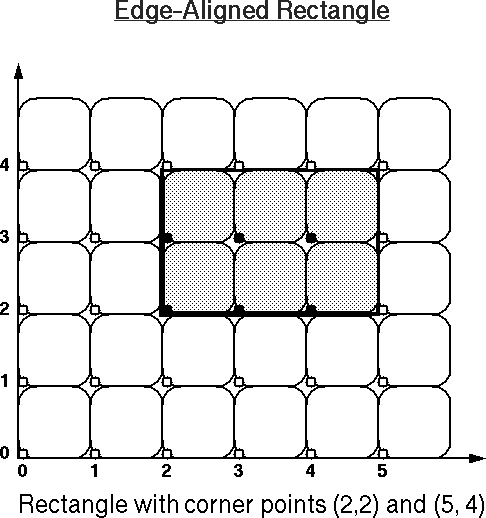
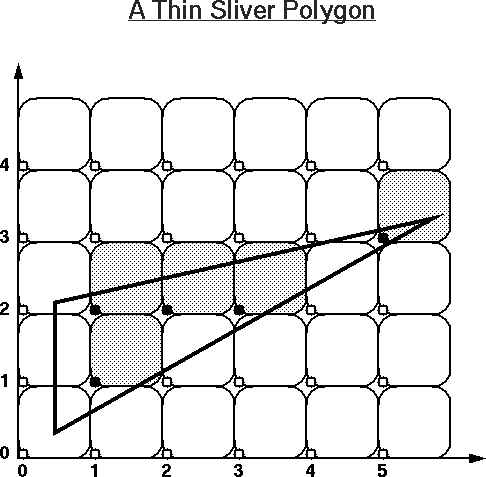
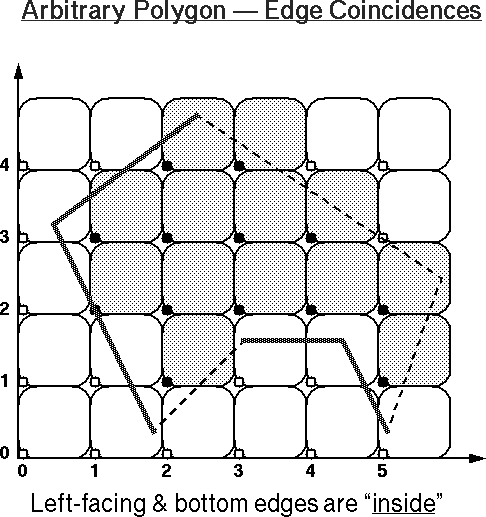
You may want to use these images as your worksheet to study other examples, or use these PostScript files for practice: