 For our purposes, an affine space a vector space offset from the origin.
For our purposes, an affine space a vector space offset from the origin.
|
University of California, Berkeley EECS Dept, CS Division |
||
| Jordan Smith |
SLIDE: Scene Language for Interactive Dynamic Environments |
Prof. Carlo H. Séquin |
| Home | Goals | Publications | People | Gallery | Assignments | Distributions |
A vector space is a set of vectors which have a vector addition (u+v) and a scalar multiplication (cv). The vector spaces we will use most commonly in graphics are R2 and R3, the 2D and 3D real coordinate systems.
 For our purposes, an affine space a vector space offset from the origin.
For our purposes, an affine space a vector space offset from the origin.
We can represent points and vectors in an affine space by adding an extra coordinate. For points, this coordinate will be 1, for vectors it will be 0. So, in 2D the point, p at (1,1) will be written p=(1,1,1), but the vector v at (1,1) will be written v=(1,1,0).
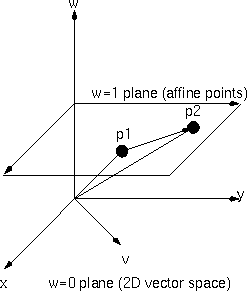
You can visualize the 2D affine space as the w=1 plane in a 3-dimensional (x,y,w) space.
You can subtract points to get vectors (p1-p2=u), and you can add vectors to points to get other points (p1+u=p2), but you cannot add two points together in an affine space. (p1+p2 is outside the affine plane),
| Type | Column Vector Matrix | Row Vector Matrix | Properties | ||||||||||||||||||||||||||||||||
Rotationrotate (0 0 1) (a)
|
|
|
Rigid Body Orthogonal |
||||||||||||||||||||||||||||||||
Scalescale (sx sy 1)
|
|
|
Non-Rigid (does not preserve length/volume) | ||||||||||||||||||||||||||||||||
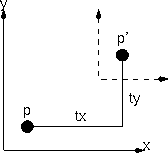
Translationtranslate (tx ty 0)
|
|
|
Rigid Body Orthogonal Submatrix |
|
x' = x + tx y' = y + ty |
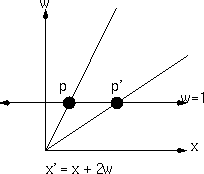
Translation can be written as a shear in an affine space. |
 |
 |

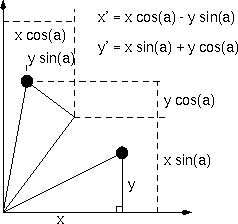
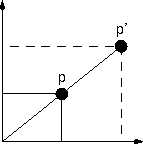
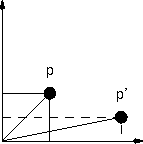
In the figure on the right, the point p is rotated by an angle
a to the point p'.
You could think of the same transformation as rotating the x-axis to x'
and the y-axis to y'.
Then the point p is in the correct rotated place with respect
to x' and y'.
| Uniform scale: p'=sp |
Non-uniform scale: x' = sxx y' = syy |
 |
 |
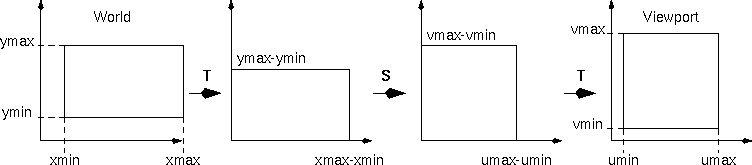
MVP,W = T(umin, vmin) * S( (umax - umin)/(xmax - xmin), (vmax - vmin)/(ymax - ymin) ) * T(-xmin, -ymin)
This page was originally built by Jordan Smith.
Last modified: Sunday, 08-Sep-2002 19:33:33 PDT