A Closed-Form Inverse Kinematics Example
The simplest non-trivial IK problem is two links and two angles, as
shown in the figure below. Say the first angle is Beavis'
shoulder. The next one is his elbow. The end of the second
link is his hand. We are going to guide the hand away from his
butt.
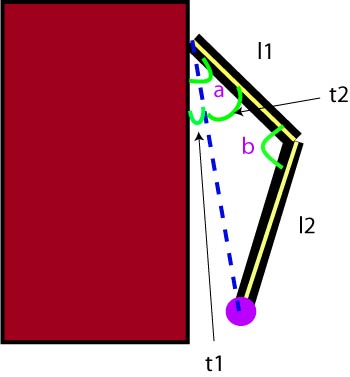
The shoulder will make an angle a with the torso. The elbow will
be bent with angle b. Our goal is to reach the purple dot, which
we say is at position (x,y).
To find the solution angles a and b, we first draw a line segment
(which we will call s) from
the shoulder to the goal (the blue dotted line). This line
segment has length D where D^2 = x^2 + y^2. We also need to "temporary"
angles:
t1 - the angle that s makes
with the body
t2 - the angle that s makes with the first limb
t1 comes from the definition of tan :
t1 = atan(-x/y)
Two Notes : 1) in discussion this figure was rotated so the answer was
t1=atan(y/x).
2) we probably would need atan2 here (when coding) as it gets the sign
correct based on which quadrant our point (x,y) is in.
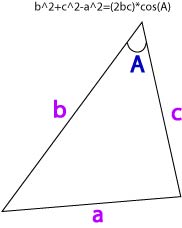Now, l1, l2, and s form a triangle. Using the
law of cosines (see figure), we get that
t2 = acos((l1^2 + D^2 - l2^2)/(2*l1*D))
a = t1+t2 // from the law of duh
b = acos((l1^2 + l2^2 - D^2)/(2*l1*l2)) // law
of cosines again
And
voila. Beavis is no longer scratching his butt.
More information including a 6-bar (not closed form) example can be
found here.
- D.P.