CS 284: CAGD
Lecture #15 -- Thu 10/11, 2012.
PREVIOUS
< - - - - > CS
284 HOME < - - - - > CURRENT
< - - - - > NEXT
Preparation: Read: SB'10: An intuitive explanation of third-order surface behavior.
Warm-up Questions:
What are principal curvatures?
What is the second fundamental form?
What is the curvature tensor?
How would you measure _change_ of curvature?
How do you take the _complete_ derivative of curvature?
How do you like to think about the local geometry around a surface point?
Discussion of:
Subdivision Surfaces (cont.)
Everybody seems to have their subdivision algorithm working nicely: 
The construction of a subdivision surface starts with a simple
polyhedron, which is then iteratively refined and smoothed by subdivision.
The texture coordinates applied to the original polyhedron are simply
subdivided in the proportion of the topological splits executed.
Problems may arise in assigning texture coordinates, if the surface is not a simple cylindical or toroidal domain.
Whenever the genus of a surface is different from 1, then you cannot
regularly tile this surface with quad tile with all valence-4 vertices.
A cube has eight valence-3 vertices, and one geometrical vertex will have to carry different texture
coordinates for different faces,
(thus it might be better to carry the texture coordinates with each face, rather than on a shared vertex).
To model a "spherical" ball we may start with a simple cube; but the "cubist" fish shape will extend beyond a single face and overlap into two adjacent faces.
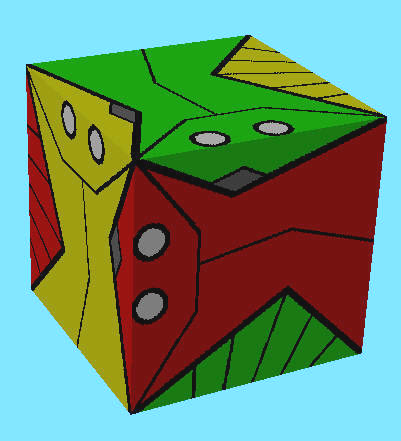
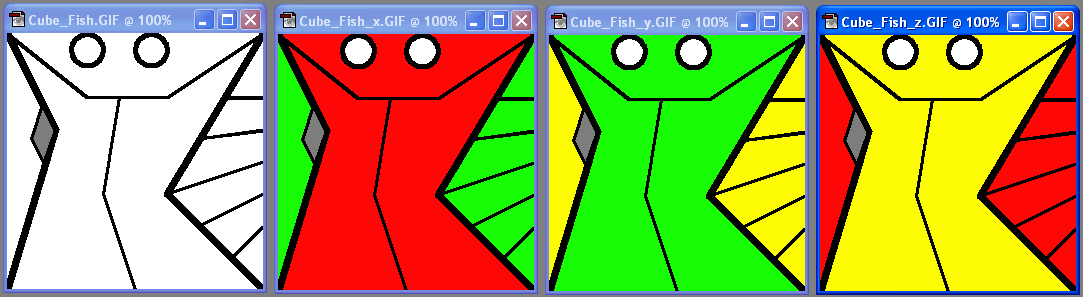

Thus the "fish" texture pattern that get's cut out by any cube face is
missing the nose and the tail, but gets those two pieces stuck in from
the two sides.
Since
these pieces belong to some other fish, they be be of different colors;
different cube faces may have different combinations of colors.
Thus, multiple copies of one B&W texture outline, filled with
different colors, are needed for the different sides of the cube.
On the cube itself, the texture coordinates will then have to be
rotated so that a seemless connection between the different patterns
and colors occurs.
In some cases, some of the tiles may also have to be mirrored! (See the actual texture coordinates used).
Here is another textured example of genus 2. -- And another one of genus 3.
More complex examples of a genus 5 surface are discussed here.
Here are some actual, Escher-tiled objects, fabricated on a Fused-Deposition Modeling (FDM) rapid prototyping machine.

Escher tiling with 12 lizards
(tetrahedral symmetry)
|

Escher tiling with 24 birds
(octahedral symmetry)
|

Tiling with 60 butterflies
(icosahedral symmetry)
|

48 starfish on genus-7 surface
|
Issues Arising with Texture Mapping:
What factors affect the quality of the generated texture?
How do the sizes of the triangles in the original (level 0) mesh affect the outcome of the generated texture pattern?
Can you use the "fish" tiles shown above to texture-map your mug? -- What issues might arise?
How would you have to modify the tiles to be able to texture-map an infinite plane?
Example pictures of triangle tiles with different sides:


Your Project Ideas ...
A Current Modeling Research Problem
How to smoothly undo a Klein bottle mouth of the "Inverted Double-Sock" type into a twisted tube with a figure-8 profile?
Some pictures to explain the problem ...
Keep this problem in mind next week when we discuss surface "optimization" (deformation while minimizing some functional).
Assignments for Tue. Oct. 16, 2012:
Read: Ken Brakke's "Surface Evolver" [ skip Sections 3.4, 3.5, 4.2, 4.8, 5.4, 5.5, 6.2, 6.7, 9, 10.]
Read: Henry Moreton's "Functional Optimization for Fair Surface Design".
Programming: Continue implementing your dyadic triangle subdivision:
1.) Add some rounding/smoothing scheme and demonstrate it on your mug.
Send me pictures by Tuesday, October 16.
2.) Add some "interesting" texture, i.e., the tiles should have some
"directionality" and not fit together with arbitrary rotations or with
every possible pairing of sides. For instance, try to use the square
"fish" tile or the triangular "lizard tile" shown above.
Get this to work by Tuesday, October 23.
COURSE PROJECTS:
By Tue, Oct. 16, e-mail me a couple of proposals (a few sentences) of what you would like to do.
PREVIOUS
< - - - - > CS
284 HOME < - - - - > CURRENT
< - - - - > NEXT
Page Editor: Carlo H. Séquin










