Requirements for Rasterization
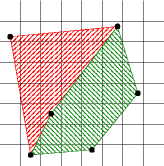 Input:
Input:
-
A set of polygons each of which is designated by a list of vertices. Each
polygon and each vertex may be assigned a color.
-
A pixel grid. The pixel designated (x,y) represents the area [x,x+1]
by [y,y+1].
On the right is an example of the input: the polygon outlines are shown
overlaid on the pixel grid,
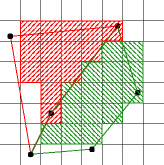 Output:
Output:
An assignment of pixels to polygons (as shown on the right) that satisfies
the following properties:
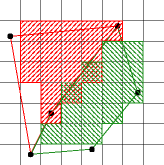 Shared Boundary:
Shared Boundary:
If two polygons do not overlap, no pixel should be assigned to both
polygons.
On the right is an example of an algorithm that violates this rule.
-
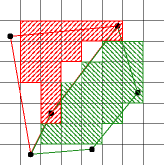 If a set of polygons completely cover a pixel, that pixel should be assigned
to one of the polygons.
If a set of polygons completely cover a pixel, that pixel should be assigned
to one of the polygons.
On the right is an example of an algorithm that violates this rule.
Sample Point Algorithms
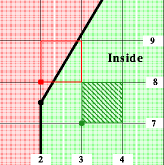
A sample point algorithm determines which polygon should contain a pixel
by sampling the polygon at one point. If that one point is contained in
the polygon, then the pixel is assigned to that polygon.
In this case, the sample point is the lower left corner of the pixel.
The polygon in question lies to the right of the edges pictured The green
pixel, pixel(3,7), which covers the region [3,4]X[7,8]
has sample point
(3.0,7.0). This sample point lies within the
polygon, therefore that pixel is assigned to the polygon.
The sample point (2.0,8.0) for the red pixel,
pixel(2,8),
is not contained by the polygon so that pixel is not assigned to that polygon.
Special cases
When a sample point lies on an edge or vertex of a polygon, we must take
care in choosing whether to assign the pixel to that polygon. Since multiple
polygons can share an edge or vertex without overlapping, it is possible
that we might accidentally assign that pixel to more than one of these
polygons.
An example algorithm
You can check out the results of a sample point algorithm for scan conversion
implemented in java at http://www.cs.berkeley.edu/~laura/cs184/scan/ScanTest.html
The pseudo-code
for that algorithm is also available.

Last modified: Wed Mar 18 12:59:36 1998
 Input:
Input: Input:
Input: Output:
Output: Shared Boundary:
Shared Boundary: If a set of polygons completely cover a pixel, that pixel should be assigned
to one of the polygons.
If a set of polygons completely cover a pixel, that pixel should be assigned
to one of the polygons.
