Procedures for Unimorph Actuator Characterization:

Here, the actuator is modeled as a mass-spring-damper system as shown below.

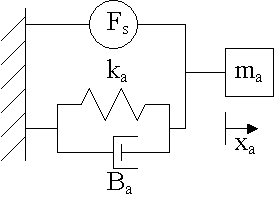
(NB: When steady-state measurements are made, only stiffness parameters appear (dampers in the model can be removed and masses simply become rigid links).

1) Ensure that there is no short circuit across the electrodes. Often, the short can be fixed simply by running a knife blade over the edges where they may occur.

2) Pole the actuator with positive polarity on the piezo side. Poling voltage will depend on piezo material and thickness (e.g., typically pole 0.125mm thick PZT at 300V).

3) Ensure actuator base is rigidly mounted at base before taking measurements. Apply 150V, then measure and record the displacement, x_DC of the actuator distal end. NB: Using the highest magnification on the appropriate lens and observing the motion on the Sony Trinitron monitor, take calibration as 1 mm on monitor=7.23 mm actual.

4) With piezo side facing upwards, note position of actuator distal end for 0V. Apply a known mass, m, to tip of actuator and measure the displacement, Dx. Calculate and record stiffness as k_a=m g/Dx.

5) Slowly increase the voltage to V_a, the point at which the distal end returns to the original position. Calculate and record blocked force as F_b=m g (150V/V_a). Remove the mass.

6) Perform a frequency sweep to determine the resonant frequency keeping in mind the following:

a. To prevent overstraining, start with low voltage amplitude since Q may be high.

b. Apply a positive offset bias to prevent depoling of unimorph.

7) Determine where V_AC is the pk-pk voltage and x_AC is the displacement range.

8) The energy product @150V, effective actuator inertia and effective actuator damping will automatically be calculated:

Procedures for Thorax Characterization:

Here, the dynamics for the actuator coupled to a single 4-bar is modeled as shown below.

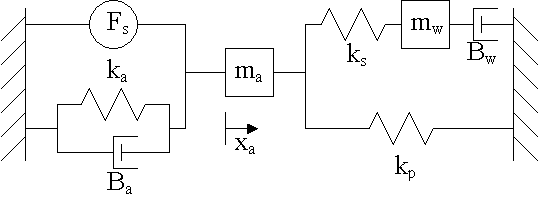
1) Apply 150V DC to both actuators and record the changes in actuator displacements (x’_DC) and output spar angles (q’_DC). (NB: The effect of differential coupling between the two spars is reduced by driving both actuators simultaneously.) The transmission ratio (T) and structure parallel stiffness (both in actuator coordinates and output spar coordinates) are automatically calculated: 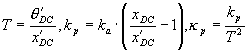. Return the voltage to zero.

2) To determine the serial compliance, move the wing by a known angle (q’’_DC) and measure the resulting change in actuator displacements (x’’_DC). (NB: Move wing in same direction as the actuator would drive it.) The series spring force can be calculated as F_s=(k_a+k_p)x’’_DC. If there were no serial compliance, the actuator should really have been displaced a distance q’’_DC/T so the series spring constant can be calculated as follows: 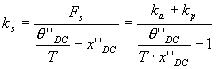. Remove the external load on the wing.

3) To determine the differential parameters, apply a known differential voltage (DV) to the two actuators. Measure the resulting actuator displacements (x’’’_DC) and the wing rotation angle (f’’’_DC). Determine the actuator displacement discrepancies as compared to the case with no rotation, the corresponding series spring force and displacement (e.g., if V₁ is applied to the leading actuator, the discrepancy is ; the spring force is F_s1=(k_a1+k_p1)Dx₁ and the overall series spring displacement is x_s1=Dx₁+F_s1/k_s1). Equating the energy stored in the wing rotation with the sum of these energies: .

CAVEAT: This energy method really only works if the series spring forces are zero when the rotation angle is zero (equivalently, if the differential was removed, the equilibrium spar positions would remain unchanged). Otherwise, the change in energy must take into consideration the pre-stressed state).

4) Drive the actuators in flapping mode (i.e., in phase) and sweep the frequency to determine the resonant frequency (observe the same precautions as in step (6) for the actuator characterization). Measure the output angle amplitudes for each spar.