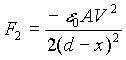 .
.EE290g Homework #5 Solutions
1.Given a parallel plate electrostatic actuator of area A and a linear spring with constant k which holds the two plates apart by a distance at rest (with no applied voltage):
a. Show that the plate can be electrostatically actuated to stable equilibria only between d and 2/3 d.
The force due to the spring is ![]() . The electrostatic force is
. The electrostatic force is 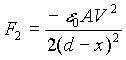 .
.
The total force on the plate is  .
.
In equilibrium, the sum of the forces is 0, so 
In stable equilibrium, a small perturbation in x will lead to a restoring force, so

but 
 , so d-x>2x, therefore
, so d-x>2x, therefore  . Also, the electrostatic force always pulls down, so
. Also, the electrostatic force always pulls down, so ![]() . This means that the gap is always between d and 2/3d.
. This means that the gap is always between d and 2/3d.
b. Calculate the pull-in voltage, VPI, which corresponds to the last stable equilibrium point (at 2/3 d0).
At this point, x=d/3, so the pull in voltage can be calculated from the above equations as

c. If the linear spring is made with a 2x2x100 micron polysilicon beam, and the gap is a 2x100 micron area with an initial separation of 2 microns, graph the plate separation as a function of applied voltage, d(V). (Using matlab is recommended).
The spring constant of the beam is  , and x satisfies the relationship
, and x satisfies the relationship
 . The pull-in voltage calculated from the equation in part b is Vpi = 23.1 Volts. The matlab code used to make this plot is here.
. The pull-in voltage calculated from the equation in part b is Vpi = 23.1 Volts. The matlab code used to make this plot is here.


2.Using what you know about simple beams, calculate a single matrix expression relating the forces and moment applied at the end of the beam to the deflection and rotation of the tip of the beam.
An axial force will cause a displacement  , so
, so 
The moment in the beam at any point x is ![]()
We also know that  , so
, so 

The boundary conditions specify that ![]() , so
, so ![]() . Therefore
. Therefore  , so
, so  and
and 
If the angle is small, then 

3.Calculate the pull-in voltage for a PLY1 gap-closing actuator with a PLY1 spring support, as shown below. Assume that h is large enough to ensure that the W x h plate is rigid, and all bending occurs in the L x a spring.
a. Ignoring the x forces and deflections, write down the simplified matrix describing the support spring.
The matrix describing the support spring is a submatrix of that shown in problem #2:

b. Calculate the electrostatic force and torque on the tip of the spring as a function of the applied potential and position of the tip of the spring.
The differential force for a given differential x is  .
.
If we assume that the wide plate is perfectly rigid (which is a good assumption, since the stiffness goes as the cube of the plate width), then y varies linearly from y0 at the left side of the plate, to ![]() at the right side of the plate. The total downward force is then
at the right side of the plate. The total downward force is then


The differential moment at any point is  . The total moment is the integral, so
. The total moment is the integral, so


c. Assuming L=100 um, a=2 um, d=2 um, W=100 um, t = 2 um, and h=10 um, solve for the pull-in voltage and pull-in position. You may need to use numerical methods.
This problem can be solved iteratively using matlab using the equations derived in parts a and b. One numerical method of solving this problem is using a program that does the following:
[F, M] = [F(y, theta), M(y, theta)] Calculate Fe and Me based on the deflections
[y, theta] = c [F,M] Calculate the deflections using the spring constants
Repeat loop until the results stabilize (i.e. the displacements don’t change any more).
The code I used for this numerical solution is here.
The plots below show the displacement (both y and theta) as a function of the applied voltage – the lines happen to overlap, so it’s difficult to see. The pull-in voltage calculated using this method was 11.73 volts.


d. Compare to the pull-in voltage expected using the model in part 1. Comments?
The simple model significantly overestimates the pull-in voltage, because it does not consider the angular displacement at the tip of the beam, nor does it consider the moment on the spring from the electrostatic force. The simple model gets within a factor of 2, but does not give a very accurate result.
4. Use cfm to calculate the y and theta deflection of the tip of the beam above as a function of applied voltage.
The figure below shows the deflection at the tip of the beam and at the end of the plate as a function of the applied voltage. The matlab script I used to generate this plot is shown
here.


Notice that these plots look quite similar to the plots above for the numerical solution.
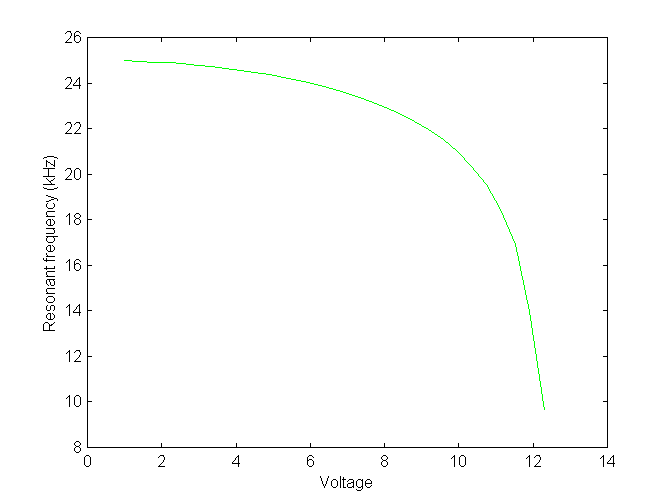
5. Use cfm to calculate the frequency of the first resonance of the system as a function of applied voltage.
The script shown above also calculates the resonant frequencies of the system as a function of the applied voltage. The figure below shows the reduction of resonant frequency as a function of the applied voltage. The resonant frequency decreases with increasing applied voltage, because the electrostatic force provides a positive force with a positive displacement (effectively a negative spring constant), and the electrostatic force increases with applied voltage. At the point of instability, the effective spring constant is zero (as is the resonant frequency).