\(\alpha\)-ReQ : Assessing Representation Quality in SSL

The success of self-supervised learning algorithms has drastically changed the landscape of training deep neural networks. With well-engineered architectures and training objectives, SSL models learn "useful" representations from large datasets without label-dependency Self-supervised learning: The dark matter of intelligence, Lecun & Misra 2021 Advancing Self-Supervised and Semi-Supervised Learning with SimCLR, Chen & Hinton 2020. Notably, when finetuned on an appropriate downstream task, these models can achieve state-of-the-art performance, often with less data than supervised models. However, the success of SSL models has its challenges. In particular, SSL algorithms often require careful model selection to avoid representation collapse Understanding self-supervised Learning Dynamics without Contrastive Pairs, Tian 2021. Further, assessing the goodness of a learned representation is difficult, usually requiring additional computing resources to train linear probes with a labeled dataset.

Task-Agnostic measures for representation quality

⊕Self-Supervised Learning algorithms for representation learning usually train multi-view encoders that embed inductive bias into the feature space via the learning objective (e.g., non-contrastive algorithms). Barlow Twins: Self-Supervised Learning via Redundancy Reduction, Zbontar 2021

The central thesis of this work explores the following

To answer this question, one must formally define the notion of goodness and examine statistical estimators that measure this property without needing downstream evaluation. Beyond theoretical interest, such a metric would be highly desirable for model selection and designing novel SSL algorithms.

In search of such a measure, we focus on one of the more efficient learning machines – the mammalian brain. The hierarchical and distributed organization of neural circuits, especially in the cortex, provides neural representations that support many behaviors across many domains. For example, to support downstream behaviors ranging from object categorization to movement detection and motor control Distributed hierarchical processing in the primate cerebral cortex, Felleman & Essen 1991 .

Recent breakthroughs in systems neuroscience enable large-scale recordings of such neural activity. By recording and analyzing the response to visual stimuli, High-dimensional geometry of population responses in visual cortex, Stringer 2018 Increasing neural network robustness improves match to macaque V1 eigenspectrum, spatial frequency preference and predictivity , Kong 2022, find that activations in the mouse and macaque monkey V1 exhibit a characteristic information geometric structure. In particular, these representations are high-dimensional, yet the amount of information encoded along the different principal directions varies significantly. Notably, this variance (computed by measuring the eigenspectrum of the empirical covariance matrix) is well-approximated by a power-law distribution with decay coefficient \( \approx \) 1, i.e., the \( n^{th} \) eigenvalue of the covariance matrix scales as 1/n.

⊕Linear regression with controlled covariates (i.e. \( \mathrm{Cov}(X) \) such that \( \lambda_i \propto i^{-\alpha} \) ) trained for fixed number of epochs. Empirical evidence suggests a Goldilock's Zone, where linear-probes enjoy better generalization.

Simultaneously, advances in theoretical machine learning provide insights into the generalization error bounds for linear regression models in overparameterized regimes. For instance, recent studies on benign overfitting in linear regression Benign Overfitting in Linear Regression, Bartlett 2019 identify that the minimum norm in the infinite-dimensional regime \( d \to \infty\) with Gaussian features interpolating prediction rule exhibits good generalization for a narrow range of properties of the data distribution. In particular, the effective rank of the covariance operator Cov(X) governs downstream generalization.

Measuring Eigenspectrum Decay & Generalization

Inspired by these results, we dig deeper into the structure of representations learned by well-trained feature encoders. One view of pretrained encoders, is that they learn mapping from high-dimensional input-spaces to a lower-dimensional manifold, say \( f_\theta : \mathbb{R}^d \to \mathbb{R}^k \) (typically \( k << d \)). Our core insight relies on studying geometric properties of the representation manifold, by examining the (centered) feature covariance matrix \( \mathrm{Cov}(f_\theta)=\mathbb{E}_x\Big[ f_\theta(x) f_\theta(x)^\top \Big] \).

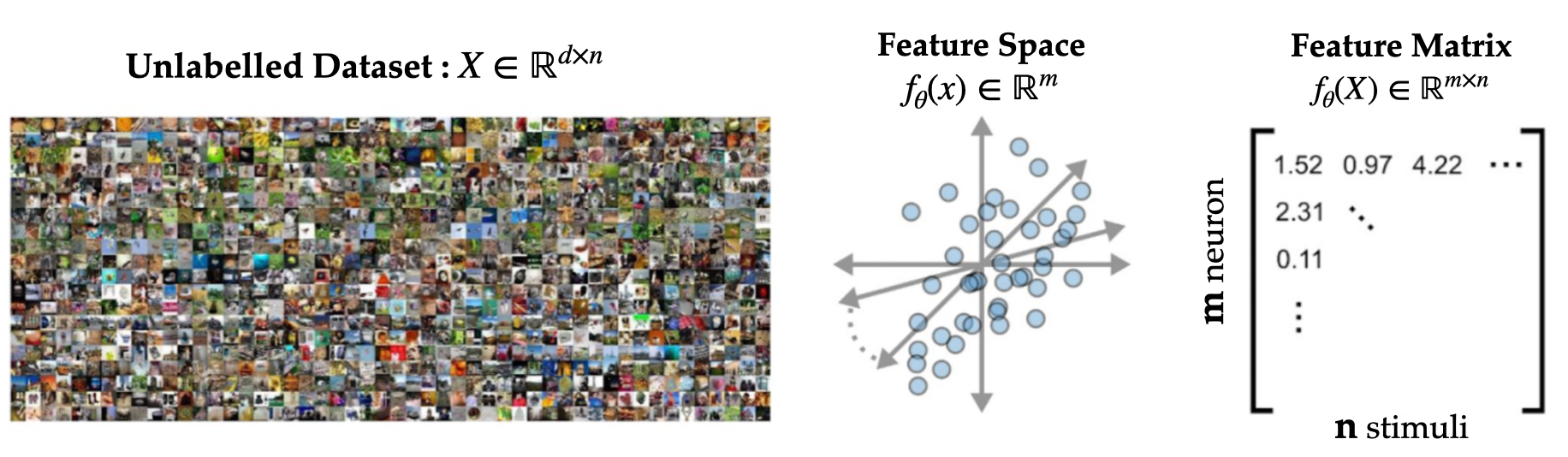
The spectral properties of \(\mathrm{Cov}(f_\theta) \) are crucial, for they inform us about the magnitude of variance in different directions in the feature space. As an illustrative example, consider the following setting: a large unlabelled dataset (say STL10) projected to a feature space with a learned encoder. Specific directions in the feature space encode more variability, often identified as the principal components of the representation. Our analysis relies on examining the eigenvalues for the covariance matrix of \( f_\theta(X) \in \mathbb{R}^{m \times n} \).

⊕Embedding high-dimensional inputs to a feature space..

Building on the intuition from linear-regression, we examine \( \mathrm{Cov}(f_\theta(X)) \) more closely across canonical neural network architectures. In particular, we probe models such as VGG Very Deep Convolutional Networks for Large-Scale Image Recognition, Simonyan 2014, ResNetsDeep Residual Learning for Image Recognition, He 2016 , ViTs (Vision Transformer) An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale, Dosovitsky 2020, pretrained on CIFAR/ImageNet datasets across different learning objectives. In particular, we compute the eigenspectrum, i.e. the distribution of eigenvalues \( \{ \lambda_1, \lambda_2, ... \lambda_n \}\) of the empirical feature covariance matrix, $$ \hat{\mathrm{Cov}}(f_\theta) = \frac{1}{N} \sum_{i=1}^{N} f_\theta(x_i) f_\theta(x_i)^\top - \Big( \frac{1}{N} \sum_{i=1}^{N} f_\theta(x_i) \Big) \Big( \frac{1}{N} \sum_{i=1}^{N} f_\theta(x_i) \Big)^\top $$ Further, to understand the role of the learning objective, we consider models with standard cross-entropy (supervised), BYOLBootstrap your own latent: A new approach to self-supervised Learning, Grill 2020, BarlowTwins Barlow Twins: Self-Supervised Learning via Redundancy Reduction, Zbontar 2021 (non-contrastive), SimCLR A Simple Framework for Contrastive Learning of Visual Representations, Chen 2020 (contrastive) pretraining.

An immediate striking observation of this experiment suggests that intermediate representations in canonical deep models follows a power-law distribution, where $$ \lambda_k \propto k^{-\alpha} $$ where \( \alpha \) is the decay coefficient. Furthermore, for well-trained neural networks \( \alpha \) is significantly correlated with in-distribution, out-of-distribution generalization across benchmark datasets such as STL10/MIT67/CIFAR10.

⊕ \( \alpha \) is predictive of out-of-distribution object recognition performance. \( \alpha \) is strongly correlated to object recognition performance on STL10 across different architectures and pretraining loss functions.

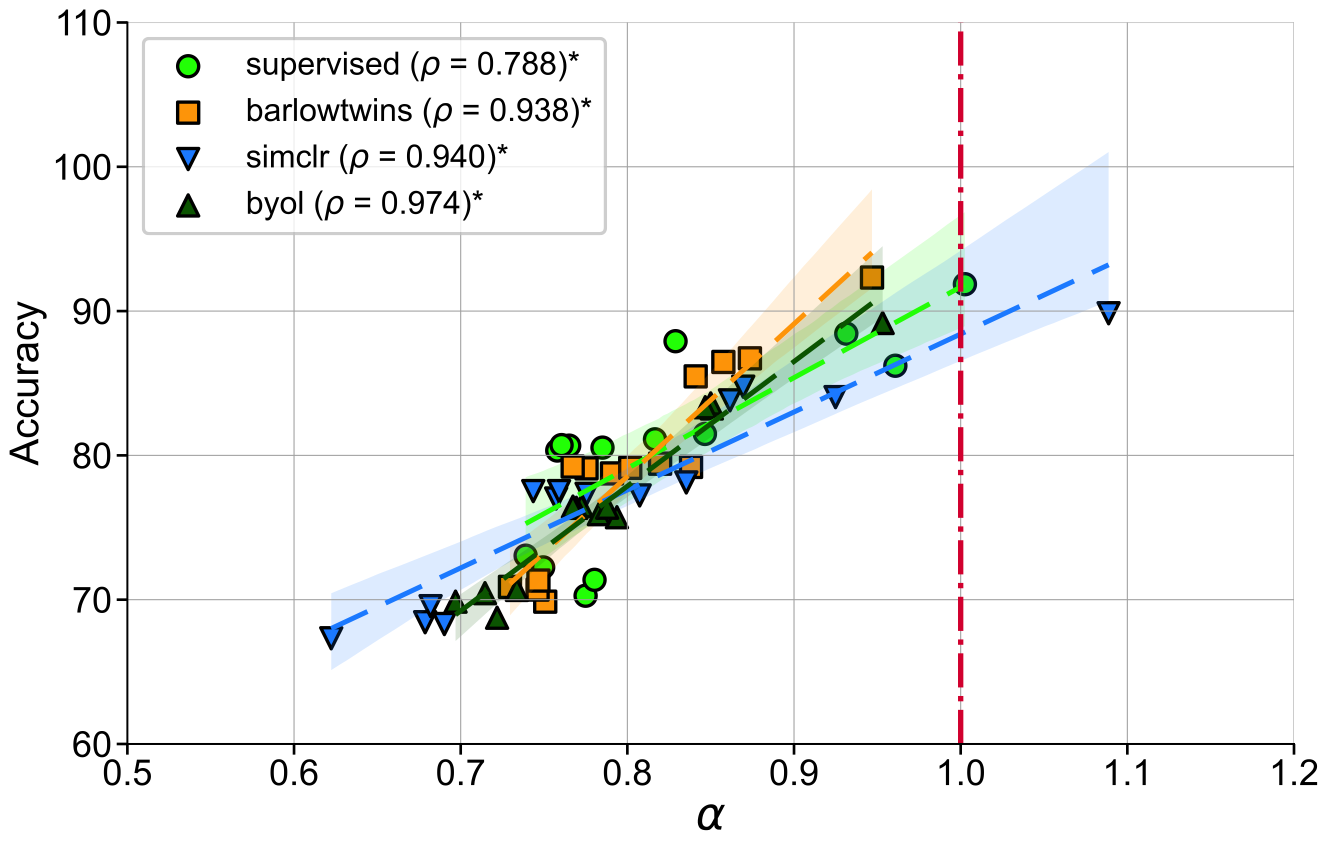
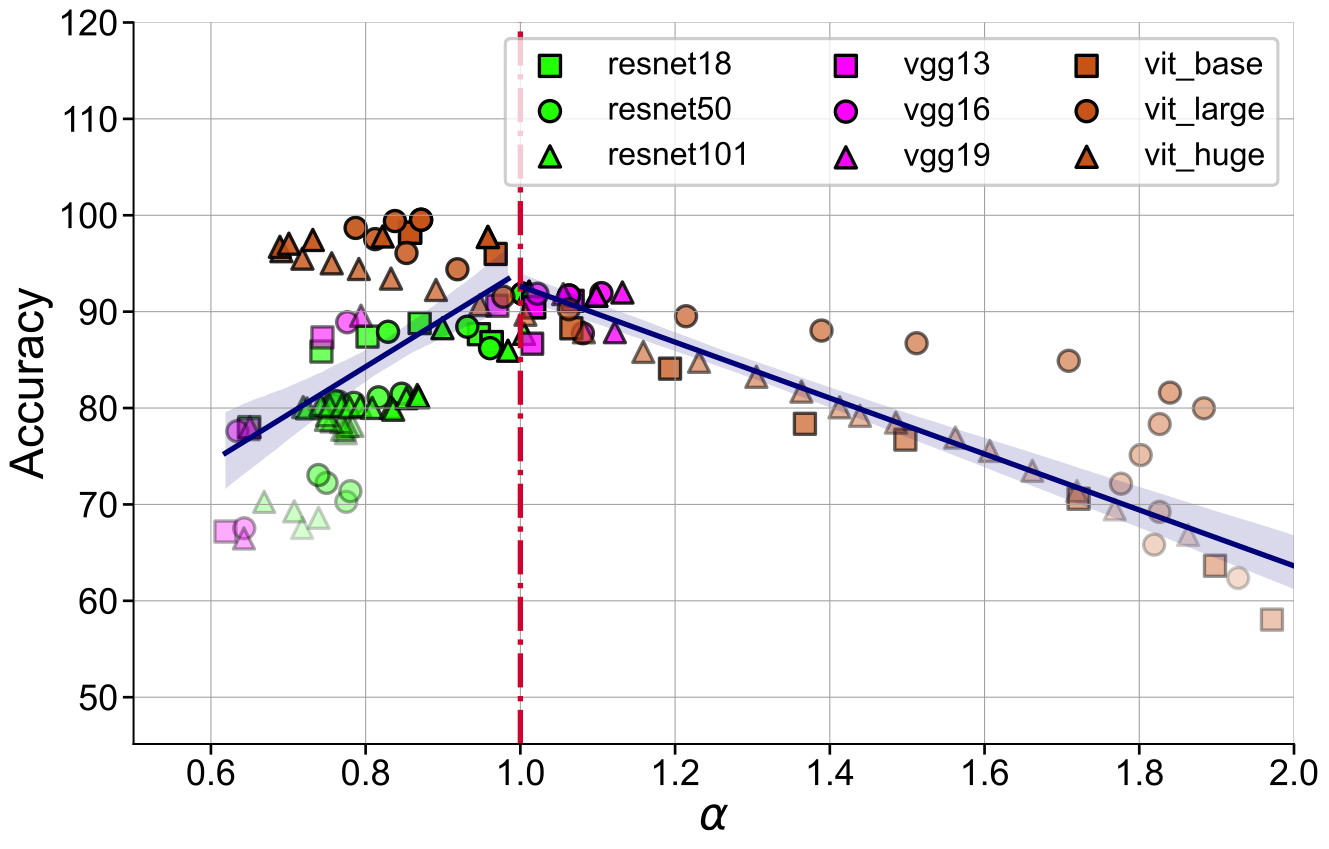
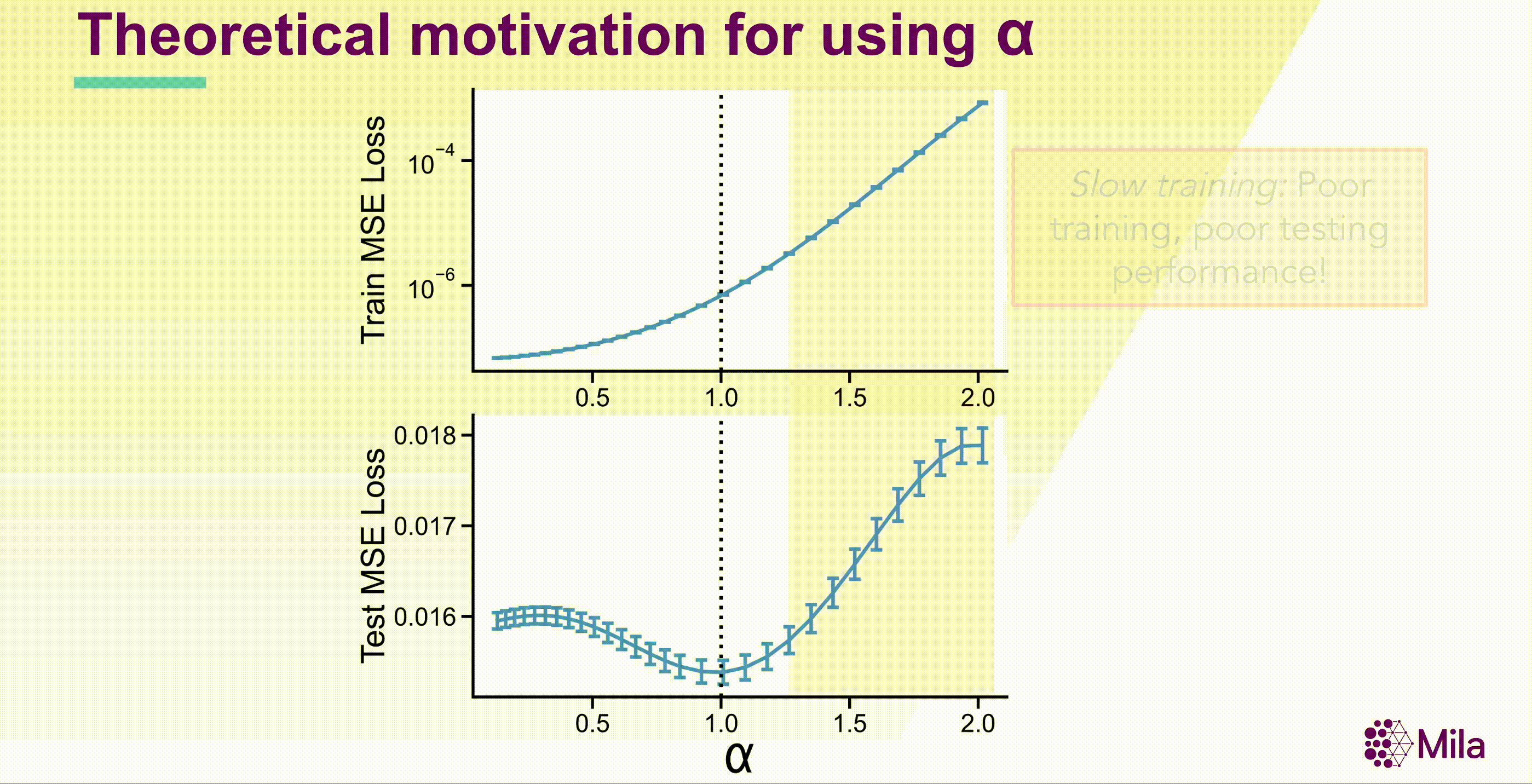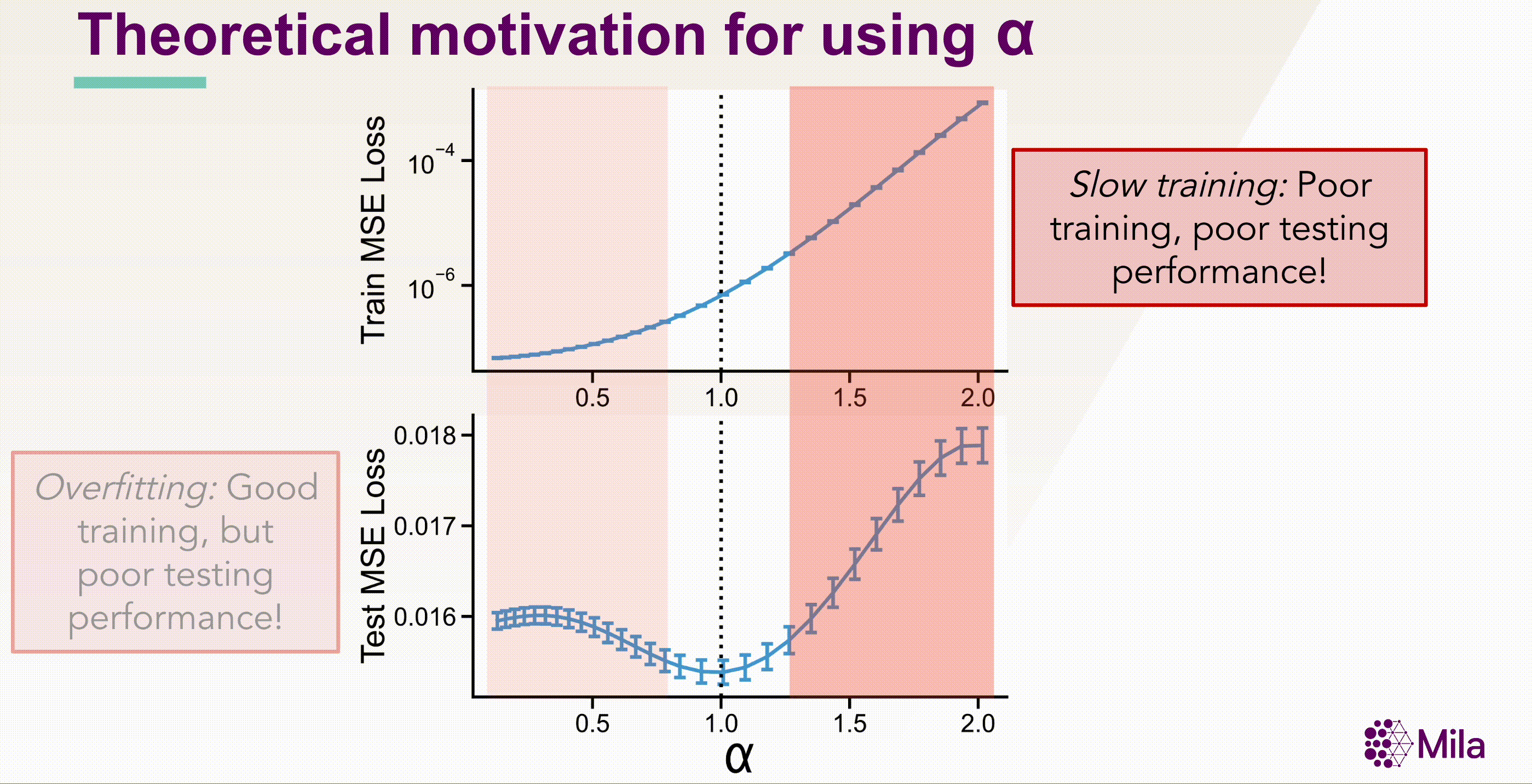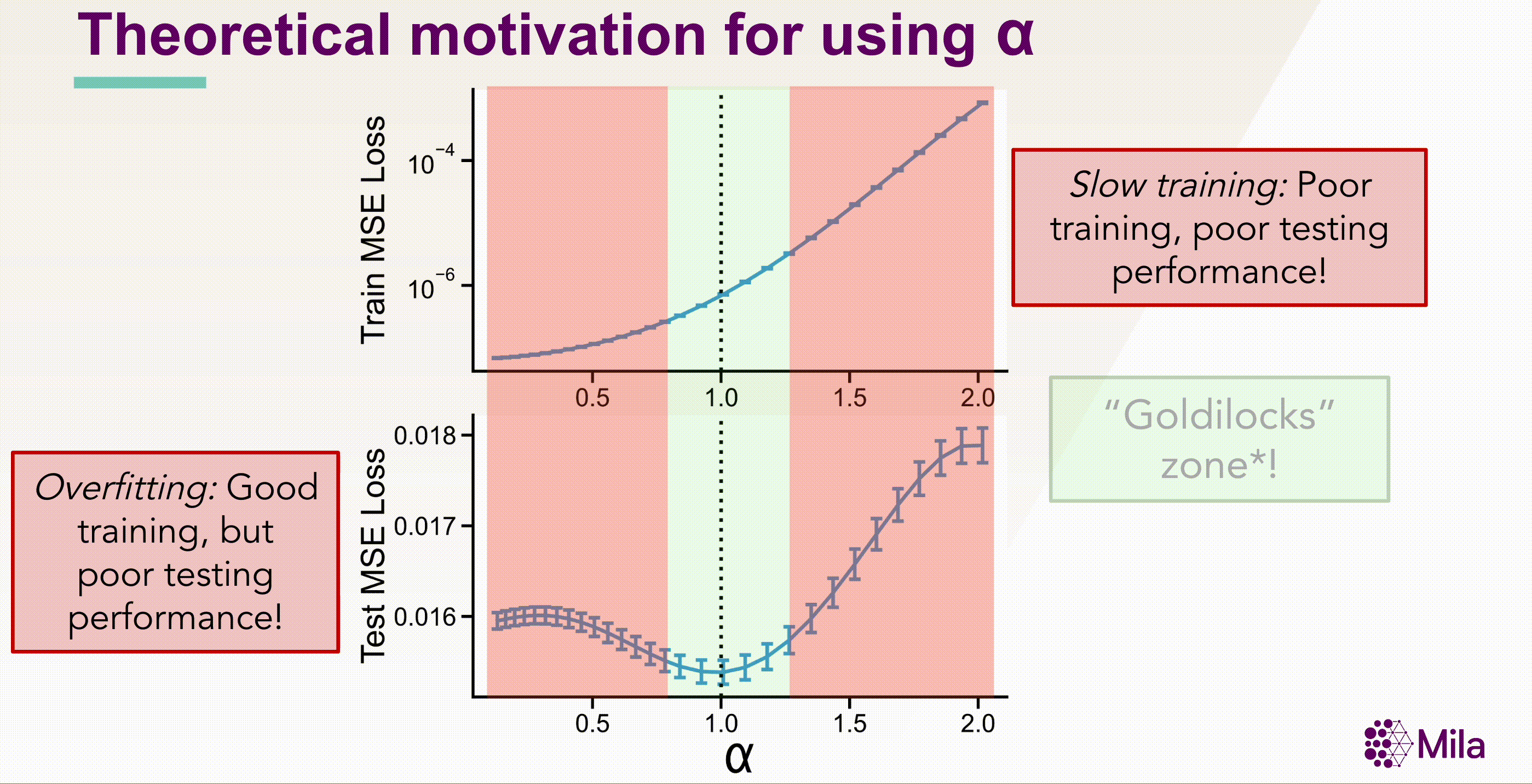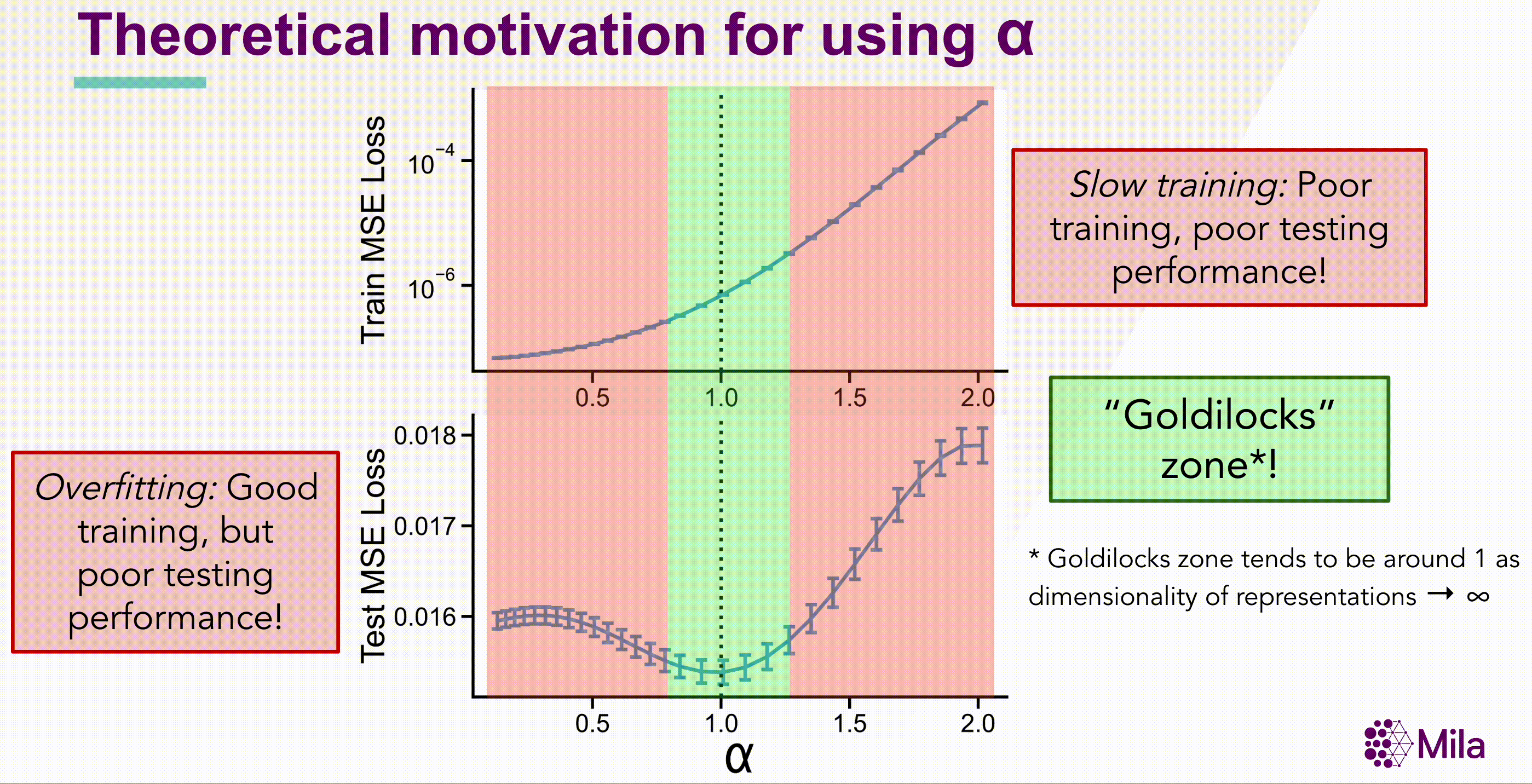
These results suggest that the coefficient of spectral decay \( \alpha \) could more generally be predictive of generalization in well-trained neural networks. Notably, \( \alpha \) is a necessary condition (not sufficient), and independent of the label-distribution and doesn't require training new modules to assess representation quality.

Mapping the Design Landscape of Barlow-Twins

With empirical evidence of \(\alpha\) being a good measure for generalization, we now wish to study its suitability as a metric for identifying the best among models pretrained with SSL algorithms. A label-free metric like \( \alpha \) could be beneficial when we don't have access to the downstream task annotations, and the SSL loss is insufficient to distinguish models with good generalization performance (see below). To investigate this, we ablate the relationship between alpha and model performance across a wide range of hyper-parameters for a representative non-contrastive SSL algorithm.

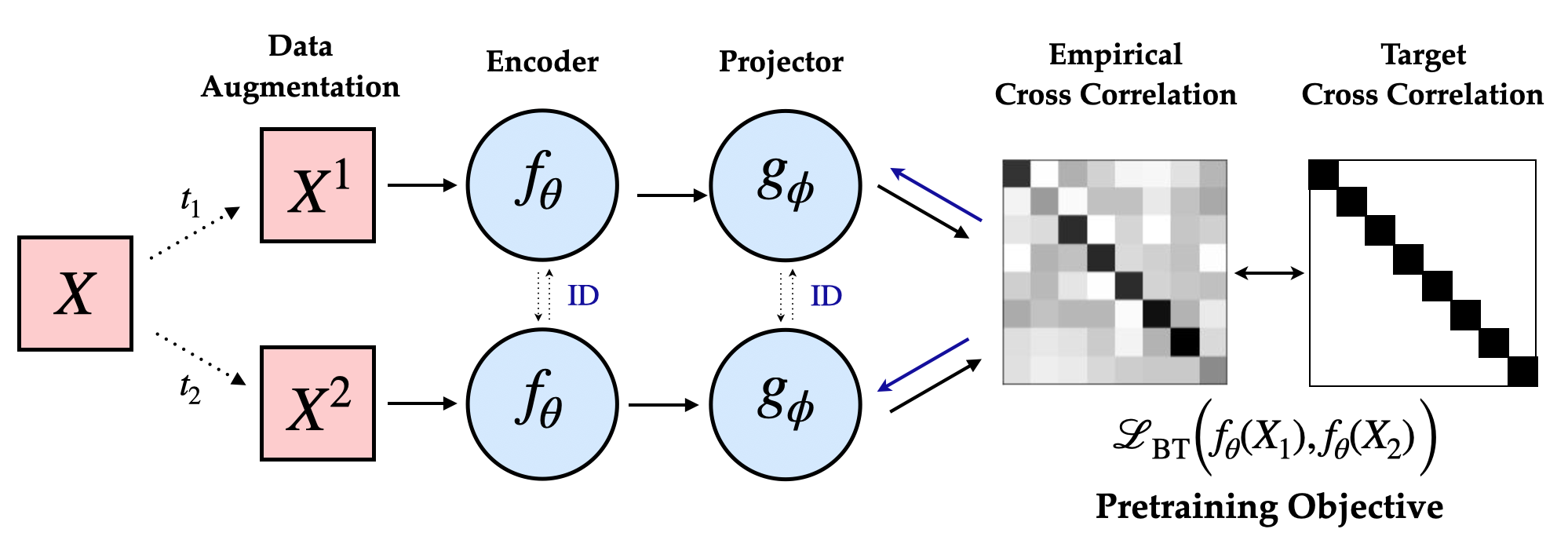
In particular, consider the Barlow Twins learning objective (\(\mathcal{L}_{\mathrm{BT}}\)) proposes imposing a \(\textit{soft-whitening}\) constraint on the cross-correlation matrix: $$ \begin{align} \mathcal{L}_{\mathrm{BT}} &= \underset{\text{invariance}}{\underbrace{\sum_{i=1}^d (1-\mathcal{C}(\mathbf{f_\theta})_{ii})^2}} + \lambda \underset{\text{redundancy-reduction}}{\underbrace{\sum_{i=1}^d \sum_{j \neq i}^d \mathcal{C}(\mathbf{f_\theta})_{ij}^2}} \\ \text{s.t. } & \mathcal{ C}(\mathbf{f_\theta})_{ij} = \frac{\sum_{n} \mathbf{f_\theta}(x^A)_i \mathbf{f_\theta}(x^B)_j }{ \sqrt{\sum_{n} \mathbf{f_\theta}(x^A)_i^2 \sum_{n} \mathbf{f_\theta}(x^B)_j^2} } \end{align} $$ where \(d\) (dimensionality of the projector head), and \(\lambda\) (coefficient of redundancy reduction) are key design hyperparameters. Furthermore, our results suggest that, unlike SSL loss, the decay coefficient (\(\alpha\)) e strongly correlates with downstream generalization across a wide range of \((d, \lambda)\).

⊕ \(\alpha \textbf{ measures representation quality.}\)
The SSL loss (fixing #gradient-steps) is no longer useful to distinguish models with superior downstream performance. However, decay coefficient \(\alpha\) strongly correlates to downstream test accuracy over an extensive hyperparameter range. Measuring in-distribution generalization for (A-C) BarlowTwins trained and evaluated on CIFAR10. (D-F) BarlowTwins trained and assessed on STL10.

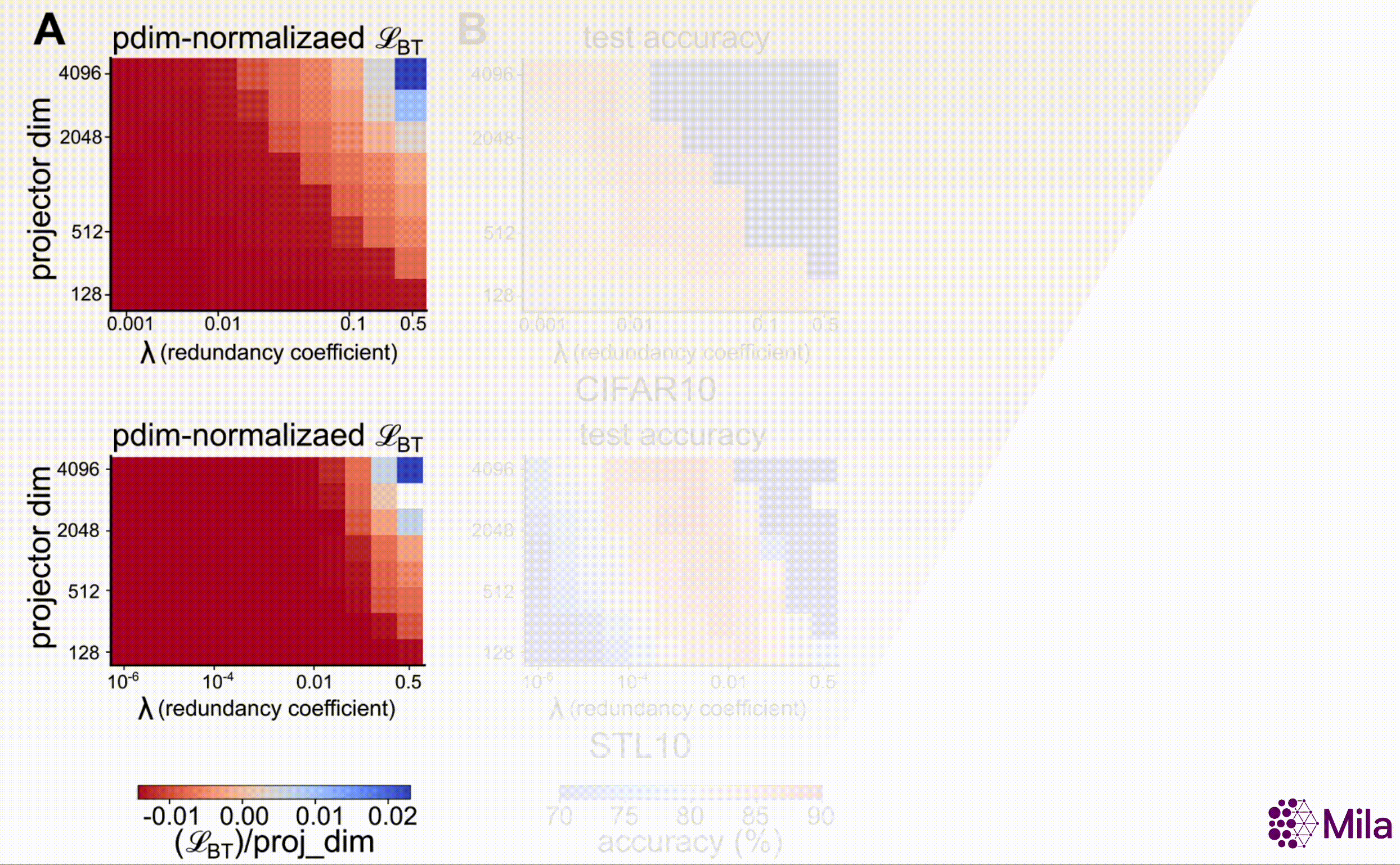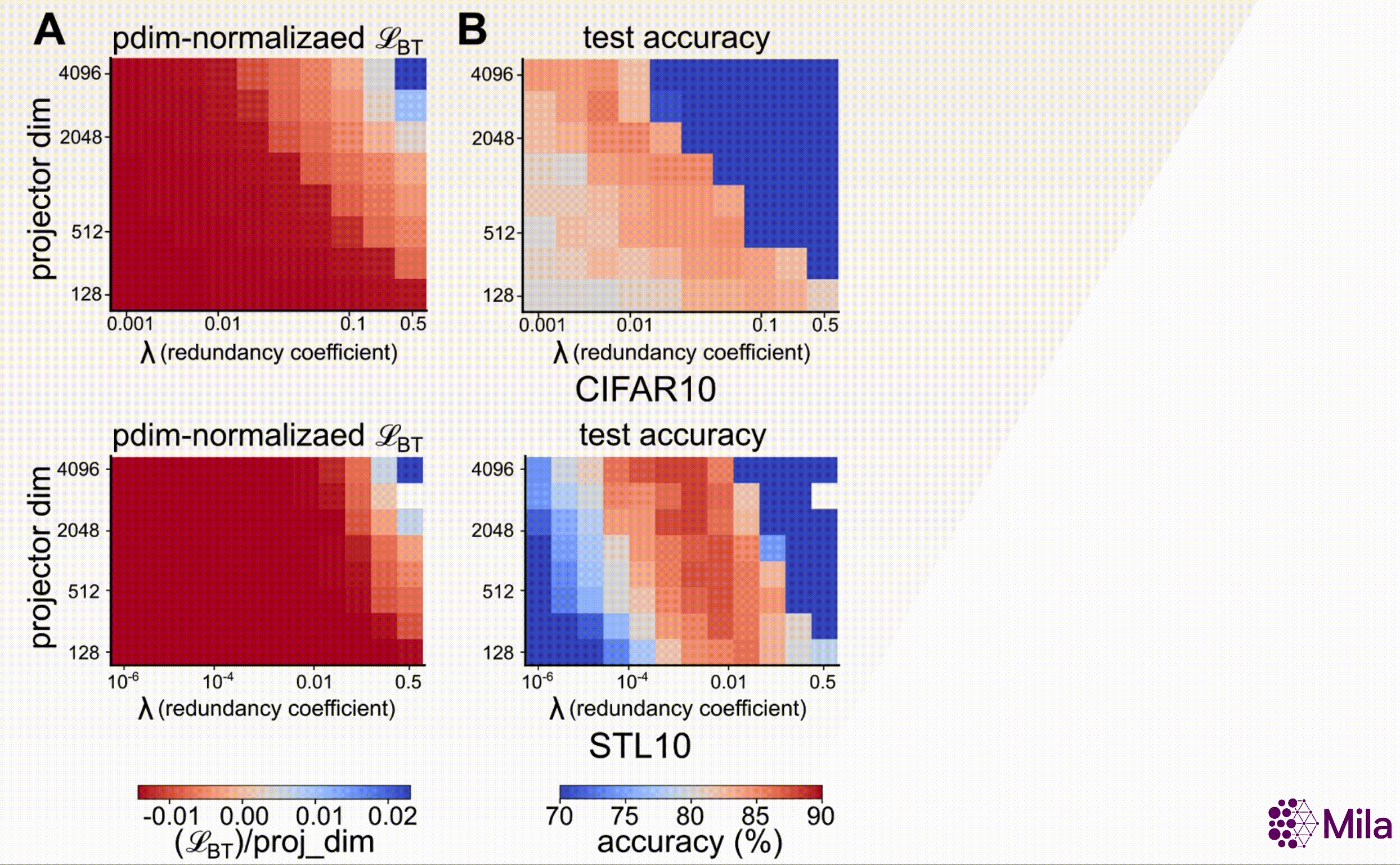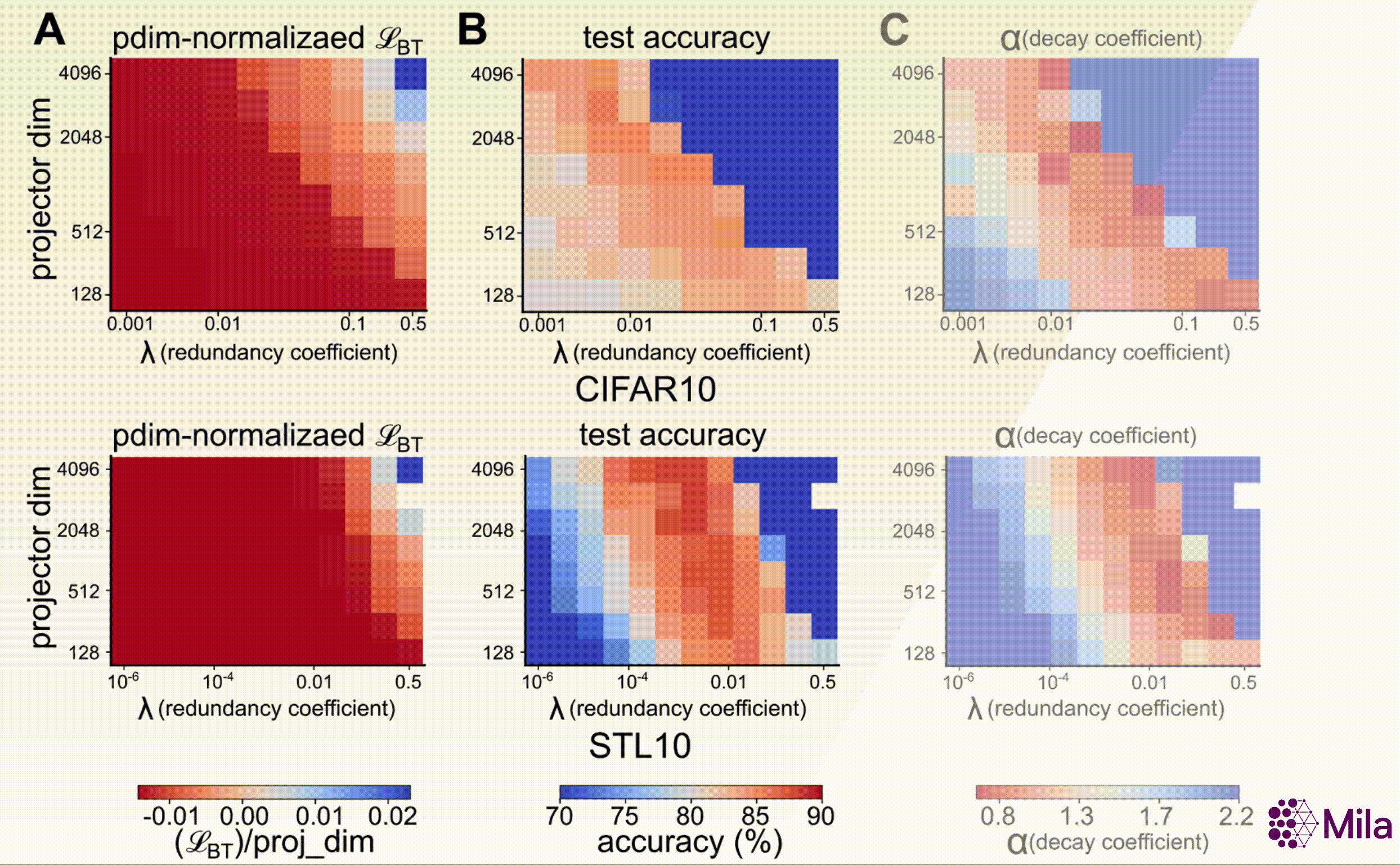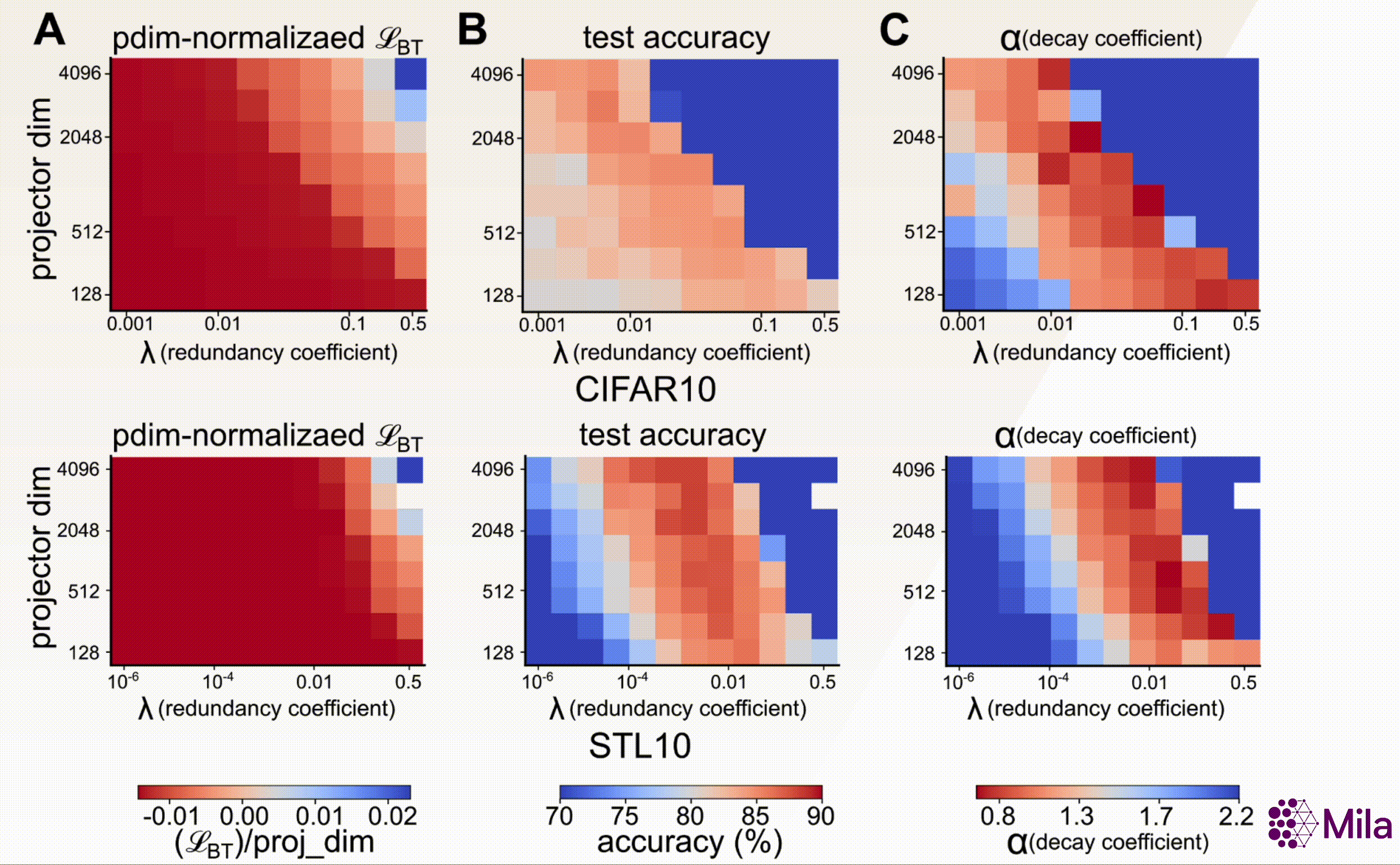
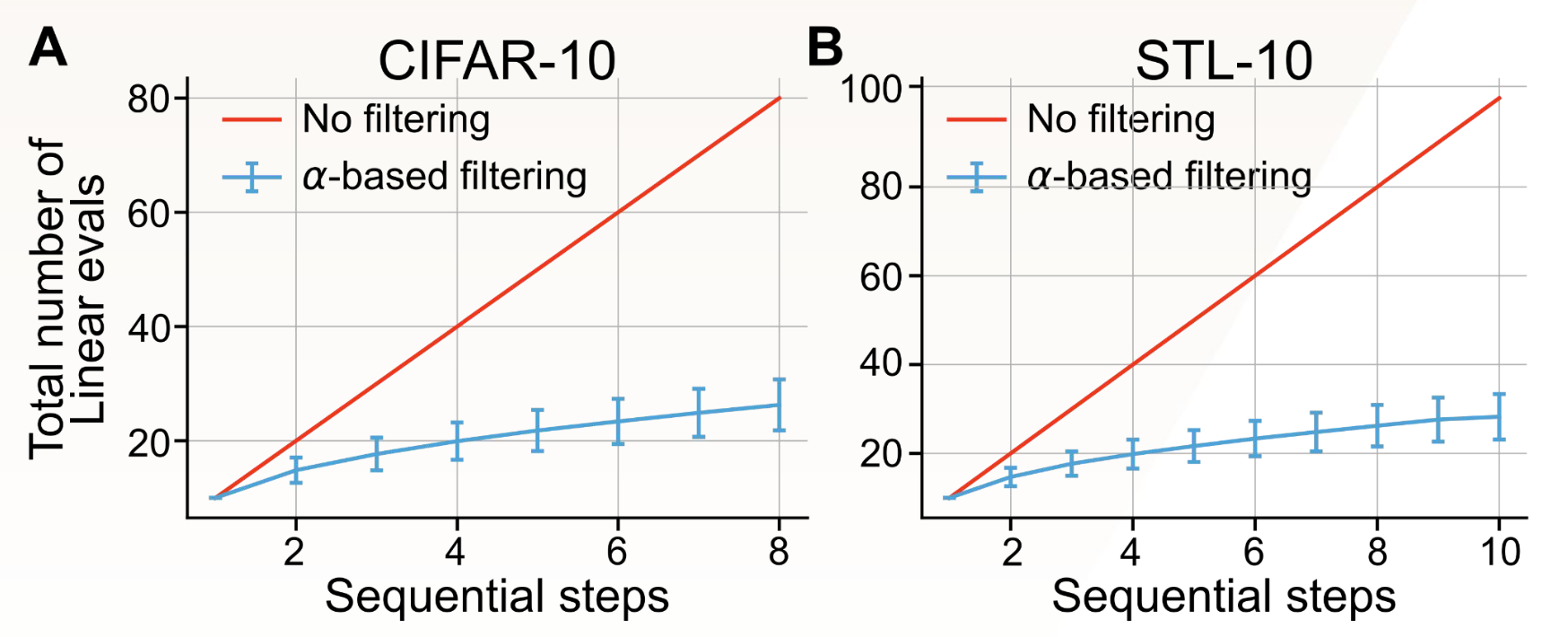
Model Selection on a Compute Budget

Learning robust representations under resource constraints has the potential to democratize and accelerate the development of AI systems. To study this, we consider the task of model selection on a compute budget. Consider a scenario where we have fixed computing to select the most generalizable model from a set of pretrained models with different hyper-parameters. In particular, we consider the setting where we can train M models in parallel and require H sequential steps to evaluate \( M \times H \) models.

The standar linear evaluation protocol would require us to train \( M \times H \) models. However, using \( \alpha \) as a necessary but not sufficient condition for generalization, we can reduce the number of models to evaluate to \( M \times \log(H) \). Summarily, the critical insight entails using α to identify the Goldilocks zone, where the model is neither redundant nor collapsed, and performing linear evaluation only for this subset of models.

⊕ \(\alpha \textbf{ as a metric to inform model selection.}\) Instead of training linear probes for each probably hyperparam, estimating the range \( [\alpha_{min}, \alpha_{max}] \) (aka the Goldilock's zone) requires logarithmic rounds of standard linear evaluation protocol.

Open Problems

Efficient measures of representation quality learned with SSL, that generalize well across a suite of downstream tasks, are still in their infancy. In this work, we identify the eigenspectrum decay coefficient \( \alpha \) as a simple statistic to approximately rank models for good out-of-distribution generalization.
Such metrics could also serve as proxies for neural architecture searchEvolving neural networks through augmenting topologies, Stanley 2002 Neural Architecture Search with Reinforcement Learning , Zoph & Le 2016. For instance, estimating \( \alpha \) on the feature embeddings for transformer architectures reveals a lower effective rank. However, a rigorous understanding of this characteristic deviation from the convolutional counterparts poses a challenging open problem.
Further natural questions include: How do we design learning objectives that implicitly or explicitly optimize these metrics during training? These are exciting research directions, we hope our preliminary investigation sparks community efforts in pursuing a principled approach to designing self-supervised neural networks.