Solutions

Problem 1. (6 points) A Miscellany.

a. AException is a superclass of BException.

b. Θ(n²).

c. We divide the proof into two separate cases: either x ≥ y, or x < y.

In the first case, we have

log (x + y) ≤ log (2x) = log 2 + log x ≤ log x + log y

The second case, where x < y, is symmetric.

log (x + y) < log (2y) = log 2 + log y ≤ log x + log y

Therefore, log (x + y) ≤ log x + log y for all x ≥ 2 and y ≥ 2, so log (x + y) ∈ O(log x + log y).

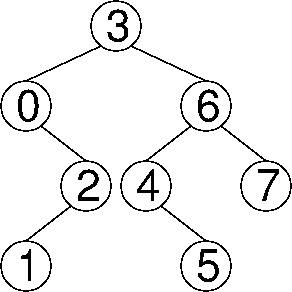
Problem 2. (10 points) Trees.

a.

b.

c. A binary heap of height h contains at least 2^h keys. A binary search tree of height h contains at least h + 1 keys. A 2-3-4 tree of height h contains at least 2^{h + 1} – 1 keys.

d.

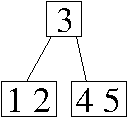
e. Write a loop that iterates through k, keeps track of the minimum key so far, and counts the number of keys in k (except k[0]) that are smaller than every previous key.

int min = k[0];
int depth = 0;
for (int i = 1; i < k.length; i++) {
  if (k[i] < min) {
    min = k[i];
    depth++;
  }
}

Problem 3. (9 points) Graphs.

a.

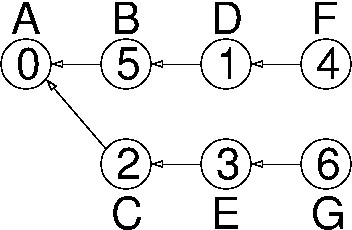
b. (6, 0)

c.

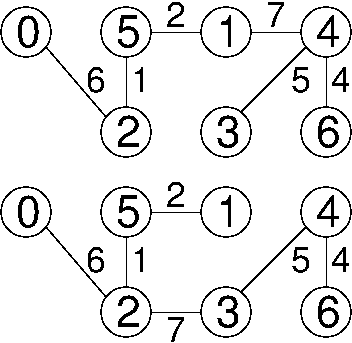
d. Do you think that T must include the edge of G with the least weight? Yes. What about the edge with the second-least weight? Yes. What about the edge with the third-least weight? No.

Kruskal's algorithm must choose the first two edges, because it is impossible that the endpoints of those edges are already connected by a path. However, the third edge is rejected if the first three edges form a triangle.

e. Θ(n² + e log e) = Θ(n² + e log n); either expression is correct.

f. Asymptotic notation is meaningful only as the number of edges e approaches infinity. In a 100-vertex undirected graph, the number of edges cannot exceed 5,050.