
Most of this collection will be "over-kill" for the majority of situations. Indeed, an 18-point cell can support a 2-inch thick f/5 Pyrex mirror that is up to 30 inches in diameter, so more than that is rarely required. However whether you have made or bought a large-diameter or ultra-thin mirror, or just dream of doing so, I hope this collection will prove to be useful, informative and entertaining.
These designs were selected based on simple (if subjective) criteria: each is "better" than a good cell with fewer support points for some particular quality. That is either it typically has less RMS error, or is simpler to construct than some reasonably good smaller cell, or is just unique in design and not outrageously bad for RMS values. In some cases, one or more alternative constructions are given if they have a certain appeal (to me) or some unique quality.
Designs that have a "v" in the name have varying angles. Designs without the "v" use default angles only (i.e. all points in each ring are evenly spaced starting from the "zero" angle). Any other appended characters indicate an alternative design. I've tried not to include too many alternatives, but simply to stick with what I feel are the "best" at each level. Other than that, the number in the name is the number of points of support.
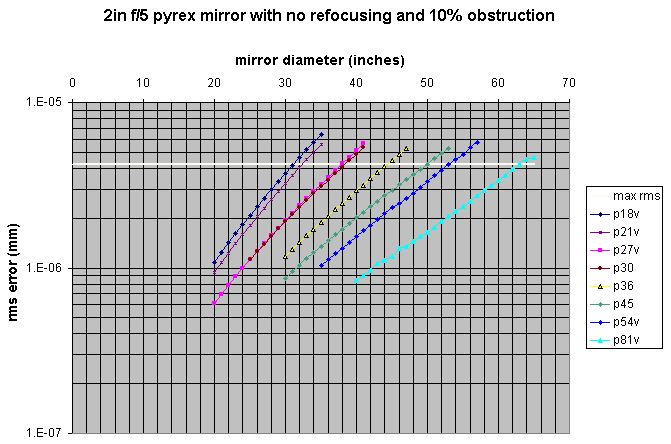
Most of these designs were selected based on a comparison of RMS error performance in two situations: a one-inch f/6 plate glass mirror, and/or a two-inch f/5 Pyrex mirror. The choice of these is somewhat arbitrary, but if I were to try and justify it, I would say that most plate glass mirrors tend to be thin, while larger Pyrex mirrors are often two or more inches thick. In any case, these situations serve as a "benchmark" for the designs that has at least some basis of reality. [Of course, these benchmarks indicate that you could support a 30x1 inch f/6 mirror on 36 points, a 36x1 inch f/6 mirror on 54 points, and a 43x1 inch f/6 mirror on 81 points, to name but a few extreme cases. If anyone builds any of these, please let me know!!]
I've also included a few "unusual" designs, with 21, 30, 45, 63, and 72 points. [Be the first on your block with a 21 point cell!] Of course, in order to be included it had to be at least as good as the next smaller design with fewer points. [For instance, I have a 42-point design that didn't make the cut, because the 36-point design was much better.] And I've also included two extra-large cell designs with 81 and 108 points that pushed the limits of my computer and GuiPlop!
In general, I tend to use varying angles, because they are typically not that much harder to construct than non-varying angle designs but also typically have much less RMS error than using only fixed angles. However in some cases the non-varying angle design is "elegant enough" to include as an alternative, or even as the only design if the gain from adding varying angles looks to be small enough not to bother. (But I could be wrong!)
I generally design with the 80:20 rule: 80% of the benefit comes from 20% of the optimization. Thus no doubt most of these designs could have a few more percent (or inches of diameter) squeezed out by various strategies. If you try it and gain more than 10-20% RMS, let me know. I will credit you in any future releases. On the other hand, at the boundary-case cell sizes of 27 and 81, where adding more points means adding more layers, you might want to try harder if a design almost but doesn't quite fits your needs. However there are more than enough designs to choose from here, that you could probably just pick one with a few more points of support. Note that the more optimization parameters there are, the longer it takes for Plop to run. In some cases, such as the 108-point cell, the design is hard to optimize and there could be better solutions than those I have benchmarked by tweaking the parameters.
Along that vein, I tend to design by "tweaking": coming up with a new starting cell of somewhat regular design and then slowly adding varying angles and radii until the gains from each new change start to diminish. That means there may be some other designs that are radically different than what I have here, either starting from a different point or taking a different approach. Also, I often start designing with a smaller number of FEM (finite element model) rings such as 12 or 20 and then slowly increase that as the design progresses. This helps the early stages to optimize faster. By no means do I claim to have the definitive result, so please be creative.
None of these designs require varying forces. I've played around with that and in many cases, adding varying forces to these designs can seemingly improve the RMS error of the design. However, I have seen in a case study of 18-point cells that varying forces need to be used with care as they can reduce the tolerance for error within the design, such that an *implementation* of the design might not be any better than that of the unoptimized design. In general, I would restrict varying forces to less than a 50% range at the most, preferably 33% or less, and even then only in a larger bar or in the large dimension of a triangle. [A 1mm positioning error in the middle of a 100mm bar is only 1% in position, but causes a 4% change in relative forces, but 10mm from the edge of a narrow triangle it is a 3.33% relative positioning error and could have a 16% or larger effect on the relative forces.] In fact, I try to avoid using very small or narrow triangles for this same reason. With all that said, a controlled use of varying forces may sometimes be useful. When I do use it and Plop tries to make the force very small on a point, I either try to relocate the point to where it will do more good, or peg the force at some fixed value greater than or equal to 0.5. It's mostly left as an exercise for the reader. On the other hand, if you have a varying force design that significantly improves performance, I'd be interested to hear.
I also tend to optimize with "Refocus Error Calculation" turned off. Refocus error compensation can generate a cell that yields a different effective focal length when pointed at the zenith and at the horizon. Thus you might need to refocus as you slew across the sky. Not good for long time exposures or extended sky-hopping observing with a single eyepiece. Furthermore, refocus error compensation often brings the support points inwards (as in the 3-point cell) and uses refocusing to compensate for the change in curvature that results. However the outer 10% of the mirror reflects 19% of the light while the inner 10% reflects only 1% of the light (assuming it is not completely shadowed by the secondary!). My case study of 18-point cells also showed that designs optimized for varying forces with refocusing on had poorer average implementation performances than cells optimized with refocusing off. Thus, on several accounts, I'd rather optimize for the support of the outer edges of mirror in all orientations. Also, I've had some occasions when "refocusing" caused erratic behavior of the optimizer when dramatically changing parameters. My hunch [there's that gut feeling again] is that if it makes a big difference then the mirror isn't being well supported, and if it doesn't make large difference, why bother. [My wife tells me I tend to over-build, but its a safe strategy to play.] "Refocus?" "Thanks, but I'll pass -- though go ahead if you like." You are welcome to try refocusing any of these designs, but I won't count it as a gain for my comparison.
Relating to secondary shadow, I adopt a more conservative 0.1 relative obstruction value (or use a more exact calculation) when I choose to use it. When computing the secondary shadow on a Newtonian, subtract the diameter of the field of view or the field stop of the largest eyepiece (e.g. 2 inches or 51 mm) from the secondary's diameter to allow for the cone of light necessary to reach the edges of the field of view. Remember, the outer 10% of a circle is 19% of the area, and the outer 30% is over half the area, so make sure that your views will stay crisp to the edge! I use the reciprocal of twice the f-ratio (1/(2*f)) as a proxy for the shadowed portion of the mirror with a Newtonian telescope having a long focal length and a full-sized secondary. For an f/5 telescope, that works out to...1/10, or 0.1. However for smaller mirrors, such as an 8-inch f/6 with 1.83-inch secondary and 2-inch focuser, there is often no unused portion of the mirror! [In general, I only use secondary obstruction for larger mirrors, such as those needing cells with 18 points or over!] For the final design run before building, I would probably compute the true shadow as well as I could, but for comparing cells, 10% works for me.
I could say more, but much of that relates to specific designs, so I will add that to the comments at the top of the files. In most cases, I've included notes there relating to my "benchmark cases" as well as some sample values in case your optimizing goes awry and you need to reset to a reasonable starting value to try again. I've sometimes included notes on the "pattern" on which the cell is based. For the numerically inclined: I've included an Excel spreadsheet with the results of the benchmark examples for most of the cells. For the visually inclined: it has graphs!
I hope you enjoy working/playing with these designs as much as I did in creating them! Please feel free to use any or all of these designs, as is, or with your own changes. NO WARRANTIES ARE EXPRESSED OR IMPLIED! However if you do build a cell based on one of these, or if you find a better cell or better parts layout for one of these sizes or within this size range, or if you just have feedback, questions, or comments, I'd love to hear from you.

To get the full package with the color gifs and the html files, upload 18pluspkg.zip [700KB] (which also contains 18plus.zip) and unzip it into the same directory that holds the zip file.
My report "A Study of 18-point Mirror Cell Optimization Using Varying Forces", is available in html and as a Microsoft Word document.
The original copy of this collection is maintained here.