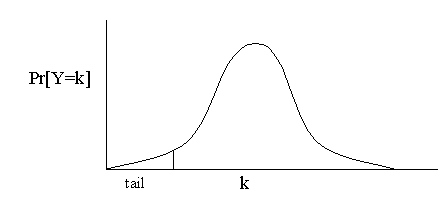
Chernoff bounds are another kind of tail bound. Like Markoff and Chebyshev, they bound the total amount of probability of some random variable Y that is in the "tail", i.e. far from the mean.

Recall that Markov bounds apply to any non-negative random variable Y and have the form
![]()
Markov bounds don’t depend on any knowledge of the distribution of Y. Chebyshev bounds use knowledge of the standard deviation to give a tighter bound. The Chebyshev bound for a random variable X with standard deviation s is:
![]()
But we already saw that some random variables (e.g. the number of balls in a bin) fall off exponentially with distance from the mean. So Markov and Chebyshev are very poor bounds for those kinds of random variables. The Chebyshev bound applies to a class of random variables and does give exponential fall-off of probability with distance from the mean. The critical condition that’s needed for a Chernoff bound is that the random variable be a sum of independent indicator random variables. Since that’s true for balls in bins, Chernoff bounds apply.
The first kind of random variable that Chernoff bounds work for is a random variable that is a sum of indicator variables with the same distribution. That is, if Xi is a random variable with Pr[Xi = 1] = p, Pr[Xi = 0] = (1-p), and the Xi are all independent, then Xi is called a Bernoulli trial. So tossing a coin is a Bernoulli trial. So is the event that a randomly tossed ball falls into one of n bins (p=1/n). If
![]()
Then X has a Binomial distribution. We derived this already for coins and balls into bins. It is
![]()
The name binomial distribution comes because of the binomial coefficients that appear in the expression for the probability.
There is a slightly more general distribution that we can derive Chernoff bounds for. If instead of a fixed probability we allow every Xi to have a different probability, Pr[Xi = 1] = pi, and Pr[Xi = 0] = (1-pi), then these event are called Poisson trial. A Poisson trial by itself is really just a Bernoulli trial. But when you have a lot of them together with different probabilities, they are called Poisson trials. But it is very important that the Xi must still be independent.
That leads us to one statement of the Chernoff bound. Let X1, X2,…,Xn be independent Poisson trials with Pr[Xi = 1] = pi. Then if X is the sum of the Xi and if m is E[X], for any d ,
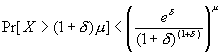
The right-hand side of this inequality looks very strange. At first its not clear that the probability is even less than one. But it is because ed < (1+d )(1+d ) for any positive d . By proving that, we will get the bound into a more comfortable (but not quite as strong) form. First, write the RHS as
![]()
Lets concentrate on the exponent inside the parenthesis, that is:
d
- (1 + d )ln(1 + d )After Taylor expanding ln(1+d ), we get
d
- (1 + d )(d - d 2/2 + d 3/3 - d 4/4 + …)which becomes
d - (d + d 2/2 - d 3/6 + d 4/3.4 - …) = -(d 2/2 - d 3/6 + d 4/3.4 - …) » -d 2/2 for small d
To give a concrete bound, if d <2e-1, this series is less than -d 2/4, so we can write
![]()
For d in that range. Normally, delta should be small, because Chernoff is about getting good bounds near the mean. If d is outside that range, we can use another simplification:
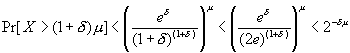
So we still get exponential decrease in probability away from the mean.
A slightly different version of the Chernoff bound applies to values less than the mean. Let X1, X2,…,Xn be independent Poisson trials with Pr[Xi = 1] = pi. Then if X is the sum of the Xi and if m is E[X], for any d in (0,1]
![]()
Once again the bound is exponential in the square of d .
Note: this proof only applies to the lower tail result. The upper tail proof is different.
First write the inequality as an inequality in exponents, multiplied by t>0.
![]()
And notice that exp(-tX) is a product of independent random variables exp(-tXi). So its expected value is the product of the expected values E[exp(-tXi)]. Now we can apply the Markov inequality to the RHS above:
![]()
Now E[exp(-tXi)] is given by
![]()
Because 1-x < exp(-x), therefore
![]()
(because the sum of the pi is m ) And the overall bound becomes
![]()
This is close to what we want, but it has an arbitrary factor of t in it. By choosing a good value of t, we can make the bound as tight as possible. It turns out that t = ln(1/(1-d )) works well. After that substitution, we get
![]()
To get the final bound, we notice that for d in (0,1]: (1-d )(1-d )>exp(-d +d 2/2)
Making that substitution gives:
![]()
Which is the Chernoff bound for the lower tail.