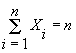
Occupancy problems deal with pairings of objects. The normal occupancy problem is about placing m balls into n bins. This seemingly uninteresting problem has a huge number of applications.
Let Xi be the random variable which counts the number of balls in bin i (so Xi is not a {0,1}-valued indicator variable. Clearly
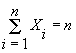
so E[å Xi] = n and by linearity of expectation, E[Xi] = 1. So we expect to see one ball in each bin, but how many bins actually have a ball in them? How many have more than one? These questions are more interesting and harder to answer. Lets define
Yj(k) = 1 if and only if bin j has k or more balls in it.
Recall that for an indicator variable E[Yj(k)] = Pr[Yj(k)=1]
Before we can compute that probability, lets compute the simpler probability that bin 1 (all bins are the same so k doesn’t matter) contains exactly i balls. That probability is
![]()
This is computed using the usual binomial formula for probability. i.e. there are n choose i ways to pick a subset of i balls that go into the first bin and the other two terms give the probability that a particular set of i balls goes there. From Stirlings formula (see page 434 of Motwani and Raghavan) there is an inequality
![]()
And when this is substituted into the last formula we get an inequality
![]()
The last term is a pretty simple bound for the probability we are looking for. But we want the probability that bin 1 contains at least k balls (i.e. that Y1(k) = 1), which is bounded by

Since the terms in brackets form a geometric series the above simplifies to
![]()
Now look carefully at the bound. Unless k>e, the geometric series we just bounded doesn’t converge, so the bound won’t work.
But for k > e, the probability of having k or more balls in a bin decreases sharply. E.g. for k=4, the probability is less than 0.66 (but this is an upper bound and the probability is not equal to 0.66). For k=6, the probability drops to less than 0.016. For k=10, it is very small indeed, less than 3x10-6. Notice that none of these bounds depend on n.
Next consider Zi = 1 if bin i contains zero balls, and zero otherwise. Now
![]()
By doing a binomial expansion of that last term, you can show that it is close to
![]()
And because Zi is an indicator random variable, we have that
![]()
So we can appeal to linearity of expectation to count the total number of empty bins:
![]()
In other words about n/e or 37% of the bins will be empty.
Here we follow the book. We place balls one at a time into bins, and compute the probability as a product of the probabilities that each ball lands in an empty bin.